2. 哈尔滨工业大学 航天学院, 哈尔滨 150001
2. School of Astronautics, Harbin Institute of Technology, Harbin 150001, China
变体飞行器能够实时感知外部环境,根据飞行环境、飞行状态与飞行任务等信息,改变自身外形特征,以提高飞行性能、控制能力和多任务能力[1-4],是未来飞行器的发展方向和研究热点,得到了国内外学者的广泛关注和深入研究[5-8]。由于变体飞行器强非线性、强不确定性、强耦合、快时变等特性以及复杂的飞行环境,增加了飞行器设计与控制的难度[9-10],及时准确地获取变体飞行器的状态信息并采取相应措施显得尤为重要。传感器作为变体飞行器感知自身状态的重要手段,一旦发生故障将会直接影响飞行控制系统的稳定性和安全性[11]。传感器监测信息的准确性直接决定了控制系统所做出的控制指令的准确性,从而影响变体飞行器的飞行性能和控制效果[12-13]。当变体飞行器的传感器发生故障时,所获取的监测信息不准确,导致控制系统不能准确获取飞行器自身状态信息,进而无法做出准确的控制指令。同时,外界扰动也会影响传感器监测信息的准确性,从而导致监测信息不完全可靠。因此,研究变体飞行器传感器故障诊断与容错控制技术具有重要的理论研究意义与实际应用价值。
文献[14]提出一种基于系统状态和控制输入估计的传感器故障检测方法,分别使用扩展卡尔曼滤波器和回溯成本输入估计方法来估计飞行器的状态和输入信息。文献[15]提出一种基于非线性虚拟传感器的故障检测、识别和恢复方法,用以估计变体飞行器的故障。文献[16]采用主成分分析和动态主成分分析技术,结合故障重构和基于证据的滤波方法,设计了一种基于数据驱动的传感器故障隔离和估计方法。上述文献对传感器故障检测与诊断问题进行了研究,能够较好的估计系统状态和故障状态,但是没有进行容错控制方法的研究,以实现飞行控制系统的稳定性。
文献[17]设计了基于T-S模糊规则的未知输入广义观测器,用以估计具有不确定性的非线性系统状态和传感器故障,同时提出一种容错控制策略来处理传感器故障,从而保证飞行器良好的跟踪性能。文献[18]针对系统的传感器故障问题,分别设计自适应多胞体观测器和自适应比例控制器,用于传感器故障诊断与容错控制,使得系统的真实输出能够较好地跟踪参考输出。文献[19]针对飞行器等时变非线性系统的未知故障和干扰,提出一种基于自适应神经滑模观测器的估计和重构方法,以保证故障诊断精确性,同时设计基于自适应神经滑模的容错控制策略,以保证故障系统的稳定性。文献[20]基于多李雅普诺夫函数和模态依赖平均驻留时间方法,设计一种有限时间H∞跟踪控制器,能够准确地跟踪系统指令。上述文献基于已有的飞行器数学模型,利用故障检测和容错控制方法,从而实现飞行器的稳定飞行。
然而,建立变体飞行器的精确数学模型难度较大,而且能够开展的实验有限,获取高价值样本信息较少,且观测数据不完全可靠。近年来,置信规则库(Belief rule base,BRB)在故障诊断领域被大量使用[21-22],BRB专家系统能够将专家知识和监测数据进行深度融合,可以处理含有模糊性、不完全性和不确定性的观测数据,提高了小样本情况下的建模精度[23]。由于在实际工程运用中,观测数据易受到干扰因素的影响,如传感器故障、外界未知扰动和噪声干扰等,导致观测数据不准确,从而降低基于BRB专家系统建模的准确度。然而,在BRB的基础上发展起来的考虑属性可靠度的置信规则库(Belief rule base with attribute reliability, BRB-r),能够较好处理观测数据所受干扰问题,有效提高复杂系统的建模能力[24-25]。在BRB-r专家系统中,由于属性可靠性反映了相关属性表示系统正确信息的能力,直接影响模型的可靠性,使用不可靠的属性会产生不可靠的模型输出。因此,BRB-r专家系统通过可靠性分析,可以减少模型误差,提高建模的准确性。
本文针对变体飞行器传感器部分失效故障,综合考虑外界扰动、变体飞行器系统模型复杂等问题,提出一种基于BRB-r传感器故障诊断与容错控制方法。首先,给出变体飞行器的气动参数模型和纵向非线性动力学模型,利用雅可比线性化方法,建立考虑变体飞行器传感器故障的切换线性变参数(Linear parameter varying, LPV)故障模型;其次,基于BRB-r专家系统分别建立传感器故障诊断模型和容错控制模型,通过可靠性分析和引入证据推理(Evidential reasoning, ER)算法,进一步地提高故障诊断精度和容错控制效果;然后,利用基于投影算子的协方差矩阵自适应优化策略(Projection covariance matrix adaption evolution strategy, P-CMA-ES)建立变体飞行器故障诊断与容错控制优化模型,对模型参数进行优化,提高故障诊断效率;最后,通过仿真验证所提方法对变体飞行器的传感器故障具有较好的容错控制效果,能够实现变体飞行器的稳定飞行。
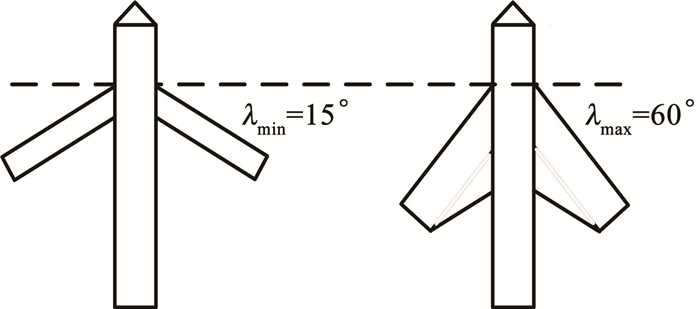
1 变体飞行器纵向LPV模型 1.1 变体飞行器纵向机理模型本文选取文献[20]中的变后掠翼飞行器为研究对象,变后掠翼飞行器结构示意图如图 1所示。变后掠翼飞行器可以改进飞行器的升力、阻力特性,使飞行器在低速和高速飞行中获得较好的性能特性。当后掠角变大时,能够减小阻力,提高临界马赫数,有利于飞行器高速飞行;当后掠角变小时,可以改善升力系数,提高飞行器巡航能力。
|
图 1 变后掠翼飞行器结构示意图 Fig. 1 Structure diagram of variable swept wing aircraft |
定义后掠角变形率表达式如下:
| $ \rho=\frac{\lambda-\lambda_{\text {min }}}{\lambda_{\text {max }}-\lambda_{\text {min }}} $ | (1) |
式中:ρ为后掠角变形率,λ为实时后掠角,λmin=15°、λmax=60°分别为后掠角的最小值和最大值,后掠角变形率的取值范围为ρ∈[0, 1]。
变体飞行器的气动参数模型定义如下:
| $ \left\{\begin{array}{l} C_{\mathrm{L}}=C_{\mathrm{L} 0}+C_{\mathrm{L} \alpha} \alpha+C_{\mathrm{L} \delta_{e}} \delta_{e} \\ C_{m}=C_{m 0}+C_{m \alpha} \alpha+C_{m \delta_{e}} \delta_{e}+\frac{c}{2 v} C_{m q} q \end{array}\right. $ | (2) |
式中:CL为升力系数,CL0为零攻角时的升力系数,CLα、CLδe分别为与攻角、舵偏角相关的升力系数,Cm为俯仰力矩系数,Cm0为零攻角时的俯仰力矩系数,Cmα、Cmδe、Cmq分别为与攻角、舵偏角、俯仰角速率相关的俯仰力矩系数。
假设变体飞行器在飞行高度h=12 500 m以Ma=0.55定值平飞,利用DATCOM软件计算不同后掠角变形率ρ下的气动参数,并通过数值拟合,得到各气动参数关于ρ的具体表达式如下[20]:
| $\left\{ \begin{array}{l} C_{\mathrm{L} 0}(\rho)=0.054 \;37 \rho^{3}-0.208 \;00 \rho^{2}+0.147 \;600 \rho-0.103 \;60\\ C_{m 0}(\rho)=0.583 \;50 \rho^{3}-2.223 \;00 \rho^{2}+1.639 \;00 \rho-0.000 \;35\\ C_{\mathrm{L} \alpha}(\rho)=-0.894 \;00 \rho+5.538 \;00\\ C_{m \alpha}(\rho)=6.138 \;00 \rho-18.070 \;00\\ C_{\mathrm{I} \delta_{e}}(\rho)=-0.000 \;53 \rho+0.006 \;50\\ C_{m \delta_{e}}(\rho)=-0.006 \;60 \rho-0.022 \;20\\ C_{m q}(\rho)=6.138 \;00 \rho-18.070 \;00 \end{array} \right. $ | (3) |
在地面惯性坐标系中,变体飞行器纵向非线性动力学方程表示如下[20]:
| $ \left\{\begin{aligned} & m v(\dot{\alpha}-q)= g m(\cos \theta \cos \alpha+\sin \theta \sin \alpha)- \\ &\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ S Q C_{\mathrm{L}}\left(\lambda, h, M a, \delta_{e}, q, \dot{\alpha}\right)+ \\ &\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \left(m_{w} \ddot{x}_{w}+m_{a} \ddot{x}_{a}\right) \sin \alpha- \\ &\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 2\left(m_{w} \dot{x}_{w}+m_{a} \dot{x}_{a}\right) q \cos \alpha \\ & I_{y} \dot{q}= S Q c C_{m}\left(\lambda, h, M a, \delta_{e}, q, \dot{\alpha}\right)- \\ &\ \ \ \ \ \ \ \ \left(m_{w} x_{w}^{2}+m_{a} x_{a}^{w}\right) \dot{q}- \\ &\ \ \ \ \ \ \ \ 2\left(m_{w} x_{w} \dot{x}_{w}+m_{a} x_{a} \dot{x}_{a}\right) q \end{aligned}\right. $ | (4) |
式中:λ、h、Ma、δe、q、α分别为变体飞行器的后掠角、飞行高度、马赫数、舵偏角、俯仰角速率和攻角,v为飞行速度,θ为俯仰角,g为重力加速度,m为飞行器总质量,S为机翼面积,mw、xw分别为机翼质量和质心位置,ma、xa分别为机翼配重质量和配重质心位置,Iy为绕y轴的转动惯量,Q为动压,c为平均气动弦长。
1.2 切换LPV模型针对变体飞行器纵向动力学模型,将含有ma、mw的项看成广义附加干扰项,通过雅克比线性化方法,并利用最小二乘方法拟合各平衡点的数据,得到变体飞行器小扰动线性化方程为
| $ \left[\begin{array}{c} \Delta \dot{\alpha} \\ \Delta \dot{q} \end{array}\right]=\left[\begin{array}{cc} -\frac{Q S C_{\mathrm{L} \alpha}}{m v} & 1 \\ \frac{Q S c C_{\mathrm{L} \alpha}}{I_y} & \frac{Q S c^2 C_{m_q}}{2 v I_y} \end{array}\right]\left[\begin{array}{l} \Delta \alpha \\ \Delta q \end{array}\right]+\left[\begin{array}{c} -\frac{Q S C_{\mathrm{L} \delta_e}}{m v} \\ \frac{Q S c C_{m \delta_e}}{I_y} \end{array}\right] \Delta \delta_e $ | (5) |
式中,Δα、Δq、Δδe分别为攻角、俯仰角速率和舵偏角的增量。
考虑外界扰动,利用离散化方法,得到含有附加干扰项的切换LPV模型为
| $ \left\{\begin{array}{l} \boldsymbol{x}(k+1)=\boldsymbol{A}_{i}\left(\boldsymbol{\rho}_{k}\right) \boldsymbol{x}(k)+\boldsymbol{B}_{i}\left(\boldsymbol{\rho}_{k}\right) \boldsymbol{u}(k)+\boldsymbol{D}_{i}\left(\boldsymbol{\rho}_{k}\right) \boldsymbol{d}(k) \\ \boldsymbol{y}(k)=\boldsymbol{C}_{i}\left(\boldsymbol{\rho}_{k}\right) \boldsymbol{x}(k) \end{array}\right. $ | (6) |
式中:x(k)为状态向量,y(k)为输出向量,u(k)为控制输入向量,附加干扰信号d(k)是L2范数有界的,Ai(ρk)、Bi(ρk)、Ci(ρk)和Di(ρk)为已知的常值矩阵,ρk为k时刻的时变参数。
不失一般性,假设(Ai(ρk), Bi(ρk))可控,ρk有界且实时可测Θ={ρ|ρ≤ρk≤ρ},ρ、ρ分别为时变参数ρk的上界和下界。将参数范围划分为若干个子空间Θi,其中i∈Γ,Γ={1, 2, …, n},n为变体飞行器的子系统个数,且满足:
| $\mathit{\boldsymbol{\varTheta}}_{i}=\left\{\boldsymbol{\rho}_{k} \in \boldsymbol{\varTheta} \mid \underline{\boldsymbol{\rho}}_{k, i} \leqslant \boldsymbol{\rho}_{k} \leqslant \overline{\boldsymbol{\rho}}_{k, i}\right\} $ | (7) |
| $ \bigcup\limits_{i=1}^{n} \boldsymbol{\varTheta}_{i}=\boldsymbol{\varTheta} $ | (8) |
| $ \bigcap\limits_{i=1}^{n} \boldsymbol{\varTheta}_{i}=\varnothing $ | (9) |
式中:Θi为变体飞行器的子系统,ρk, i、ρk, i分别为第i个子系统中时变参数ρk的上界和下界。
由于变体飞行器的飞行环境复杂,飞行条件恶劣,极易发生传感器故障,从而影响飞行性能。变体飞行器的故障可分为执行器故障、传感器故障和元部件故障,而传感器故障主要有增益变化、卡死和偏差失效。其中增益变化亦称传感器失效故障。诸如陀螺仪、加速度计、伺服机构等传感器作为变体飞行器感知自身状态的重要手段,其监测信息的准确性直接决定了控制系统所做出的控制指令的准确性以及飞行效果。因此,本文针对传感器部分失效故障,得到切换LPV故障模型如下:
| $ \left\{\begin{array}{l}\boldsymbol{x}(k+1)=\boldsymbol{A}_{i}\left(\rho_{k}\right) \boldsymbol{x}(k)+\boldsymbol{B}_{i}\left(\boldsymbol{\rho}_{k}\right) \boldsymbol{u}(k)+\boldsymbol{D}_{i}\left(\boldsymbol{\rho}_{k}\right) \boldsymbol{d}(k) \\ \boldsymbol{y}(k)=\boldsymbol{C}_{i}\left(\rho_{k}\right)(1-\lambda) \boldsymbol{x}(k)\end{array}\right. $ | (10) |
式中,0≤λ≤1为传感器失效系数。
2 变体飞行器故障诊断与容错控制模型构建文献[20]提出的变体飞行器有限时间切换H∞控制方法对微小干扰、噪声等具备一定的鲁棒性,能够保证变体飞行器的稳定飞行。但随着干扰和故障程度增加,由于鲁棒控制能力有限,导致飞行器状态产生较大波动,甚至失稳,严重影响变体飞行器的飞行性能。
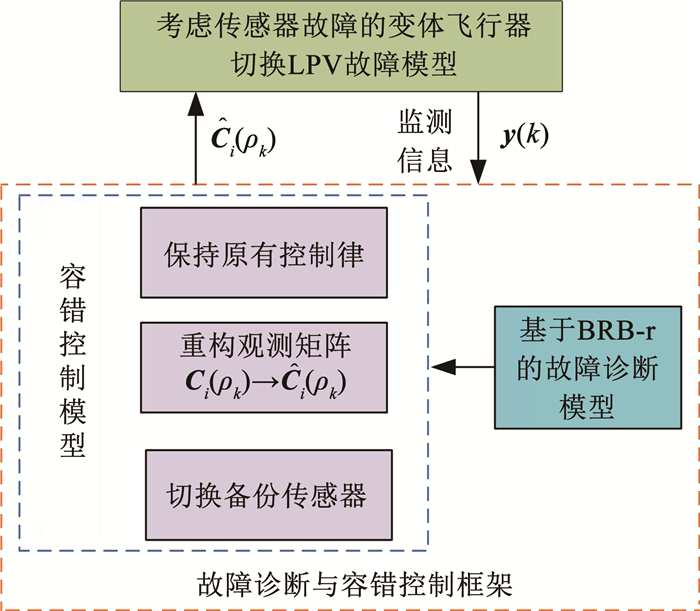
此外,由于其鲁棒性能有限,在利用变体飞行器的观测输出y(k)进行故障诊断时,故障诊断精度不能得到保证,从而降低容错控制效果。因此,本文基于BRB-r专家系统构建变体飞行器传感器故障诊断与容错控制框架,如图 2所示。
|
图 2 变体飞行器传感器故障诊断与容错控制框架 Fig. 2 Fault diagnosis and fault tolerant control framework of sensor for morphing aircraft |
可以看出,变体飞行器故障诊断与容错控制框架由基于BRB-r的故障诊断模型和容错控制模型两部分组成。首先,基于BRB-r专家系统构建传感器故障诊断模型,对变体飞行器输出状态y(k)进行故障检测和诊断,确定传感器故障状态;然后,构建容错控制模型,根据故障诊断结果,结合传感器监测信息和系统状态,重构传感器观测矩阵,以保证变体飞行器的容错控制能力和鲁棒性能。
2.1 变体飞行器监测指标可靠度分析当存在外界干扰时,传感器监测数据的准确性将会受到影响,从而降低监测信息的可靠性。目前,计算属性可靠度的方法主要有:基于专家的判断方法、最小距离法和统计方法。基于专家的判断方法不需要观测数据,可以基于专家知识来计算属性可靠度,但是其准确性会受到专家知识不确定性的影响。而最小距离法在观测数据较少时,计算的属性可靠度不准确,统计方法可以将专家知识和观测数据进行整合,从而提高属性可靠度的准确度[23]。因此,本文采用基于统计方法计算传感器监测指标的可靠度,通过构造一个容差范围以区别不可靠的观测数据,并统计一段时间内不可靠数据的个数,评估该段时间内监测指标的可靠度。
针对第i个监测指标给定监测数据波动区间(
当监测数据超过波动区间时,表示第i个监测指标的监测数据不可靠,不能完全准确反映飞行器状态,则sij=1;反之,sij=0。
因此,第i个监测指标的可靠度为
| $ r_{i}=\frac{T_{i}-\sum\limits_{j=1}^{T_{i}} s_{i j}}{T_{i}}=\frac{T_{i}-s_{i}}{T_{i}}, i=1, 2, \cdots, M $ | (11) |
式中:ri为第i个传感器监测指标的可靠度,Ti为监测数据总数,si为不可靠监测数据的个数,M为监测指标的个数。
2.2 传感器故障诊断模型构建BRB-r专家系统中输入和输出之间的非线性关系通过规则来表示,一般表达式为[23]
| $ \begin{array}{l} R_{k} \text { : If } x_{1} \text { is } A_{1}^{k} \wedge x_{2} \text { is } A_{2}^{k} \cdots \wedge x_{M_{k}} \text { is } A_{M_{k}}^{k} \text {, } \\ \;\;\;\;\;\; {\rm{Then}}\; y \;{\rm{is}} \\ \;\;\;\;\;\; \left\{\left(D_{1}, \beta_{1, k}\right), \cdots, \left(D_{N}, \beta_{N, k}\right)\right\}\left(\sum\limits_{n=1}^{N} \beta_{n, k} \leqslant 1\right) \\ \;\;\;\;\;\; {\text{With rule weight }}\; \theta_{k} , \; {\text{attribute weight}} \\ \;\;\;\;\;\; \delta_{k 1}, \delta_{k 2}, \cdots, \delta_{k M_{k}} \\ \;\;\;\;\;\; \text { and attribute reliability } r_{1}, r_{2}, \cdots, r_{M} \end{array} $ | (12) |
式中:x1, x2, …, xMk为M个监测指标的监测信息;A1k, A2k, …, AMkk为监测指标的参考等级,可以将多元信息转化到统一框架中;y为故障诊断模型输出;{D1, D2, …, DN} 为模型的N个故障状态;{β1, k, β2, k, …, βN, k} 为其相对应的置信度,由于专家知识的不完备性,规则输出结果置信度之和可能不为1,即
故障诊断模型的输入为传感器监测指标yi,即变体飞行器的控制输出。基于BRB-r专家系统构建传感器故障诊断模型,可分为如下步骤。
步骤1 计算监测数据相对于每条规则的匹配度。
在监测数据获取后,将其转换成规则的匹配度,即
| $ \alpha _i^j = \left\{ \begin{array}{l} \frac{{{c_{i, k + 1}} - y_i^*}}{{{c_{i, k + 1}} - {c_{i, k}}}}, j = k\;{\rm{ if }}\;{c_{i, k}} \le y_i^* \le {c_{i, k + 1}}\\ \frac{{y_i^* - {c_{i, k}}}}{{{c_{i, k + 1}} - {c_{i, k}}}}, j = k + 1\\ 0, \;\;\;\;\;\;\;\;\; j = 1, 2, \cdots , L, j \ne k, k + 1 \end{array} \right. $ | (13) |
式中:αij为第i个传感器监测指标相对于第j条规则的匹配度,L为规则数量,ci, k、ci, k+1分别为第i个监测指标相对于第k条和第k+1条规则的参考值,yi*为第i个监测指标的监测数据,表示变体飞行器控制输出的观测值。
监测指标相对于第k条规则的整体匹配度可以通过下式求得:
| $ {\alpha _k} = \prod\limits_{i = 1}^M {{{\left( {\alpha _k^i} \right)}^{{W_i}}}} $ | (14) |
| $ {W_i} = \frac{{{{\bar \delta }_i}}}{{1 + {{\bar \delta }_i} - {r_i}}} $ | (15) |
| $ {{\bar \delta }_i} = \frac{{{\delta _i}}}{{\mathop {\max }\limits_{i = 1, \cdots ,M} \left\{ {{\delta _i}} \right\}}} $ | (16) |
式中:αk为传感器监测指标相对于第k条规则的匹配度,δi为监测指标的相对属性权重,Wi为融合监测指标可靠度和相对属性权重后的综合指标。
步骤2 计算每条规则的激活权重。
由于监测指标对每个规则的匹配度不同,故对于每条规则的激活权重也不同,监测指标对于规则的激活权重为
| $ {w_k} = \frac{{{\theta _k}{\alpha _k}}}{{\sum\limits_{l = 1}^L {{\theta _l}} {\alpha _l}}}, k = 1, \cdots , L $ | (17) |
式中:wk为监测指标相对于第k条规则的激活权重,表示对该规则的使用程度;θk为规则权重,表示第k条规则在规则库中的重要程度。
步骤3 计算模型输出结果的置信度。
在获取规则激活权重后,由于不同的规则产生不同的故障诊断结果,故采用ER解析算法对基于BRB-r的故障诊断模型中的规则进行融合,以计算故障诊断模型输出结果的置信度,从而保证融合过程中不确定性的合理处理。ER解析算法如下[26]:
| $ {\beta _n} = \frac{{\mu \left[ {\begin{array}{*{20}{l}} {\prod\limits_{k = 1}^L {\left( {{w_k}{\beta _{n, k}} + 1 - {w_k}\sum\limits_{j = 1}^N {{\beta _{j, k}}} } \right)} - }\\ {\prod\limits_{k = 1}^L {\left( {1 - {w_k}\sum\limits_{j = 1}^N {{\beta _{j, k}}} } \right)} } \end{array}} \right]}}{{1 - \mu \left[ {\prod\limits_{k = 1}^L {\left( {1 - {w_k}} \right)} } \right]}} $ | (18) |
| $ \begin{array}{l} \mu = \left[ {\sum\limits_{n = 1}^N {\prod\limits_{k = 1}^L {\left( {{w_k}{\beta _{n, k}} + 1 - {w_k}\sum\limits_{j = 1}^N {{\beta _{j, k}}} } \right)} } - } \right.\\ \;\;\;\;\;\;{\left. {(N - 1)\prod\limits_{k = 1}^L {\left( {1 - {w_k}\sum\limits_{j = 1}^N {{\beta _{j, k}}} } \right)} } \right]^{ - 1}} \end{array} $ | (19) |
式中:βn为融合后的故障诊断输出结果中第n个监测指标参考等级的置信度,βn, k为相对于第k条规则中参考等级的置信度,μ为修正因子,N为故障诊断结果参考等级个数。
步骤4 确定传感器故障状态。
由于基于BRB-r专家系统融合后的输出结果为各个故障情况的置信度,进一步可以表示各个故障情况置信度向量为β=[β1, β2, …, βN],设置由传感器的N个标准故障向量组成的标准故障矩阵为
| $ \boldsymbol{C}=\left[\begin{array}{ccccc} C_{1, 1} & C_{1, 2} & \cdots & C_{1, N-1} & C_{1, N} \\ C_{2, 1} & C_{2, 2} & \cdots & C_{2, N-1} & C_{2, N} \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ C_{N-1, 1} & C_{N-1, 2} & \cdots & C_{N-1, N-1} & C_{N-1, N} \\ C_{N, 1} & C_{N, 2} & \cdots & C_{N, N-1} & C_{N, N} \end{array}\right] $ | (20) |
通过计算标准故障向量与基于BRB-r故障诊断模型输出结果向量之间的最短距离来对传感器开展故障诊断[11],其距离可以通过下式计算:
| $ \left\|\boldsymbol{\beta}-\boldsymbol{C}_{i}\right\|=\left(\sum\limits_{n=1}^{N}\left|\beta_{n}-\boldsymbol{C}_{i, n}\right|\right)^{2}, i=1, 2, \cdots, N $ | (21) |
式中:‖·‖为两个向量之间的范数,Ci为第i个故障的标准特征向量,由专家给定。
当第i个标准故障向量与基于BRB-r的故障诊断模型输出结果向量之间的距离最短时,即为当前时刻传感器的故障状态。
2.3 传感器容错控制模型构建针对传感器部分失效故障,基于BRB-r专家系统构建传感器容错控制模型,并根据故障诊断结果,重构故障传感器观测矩阵Ci(ρk)。在观测矩阵重构过程中,需要保证重构信息的物理意义,即要求传感器的监测信息和重构信息具有相同的物理意义,以满足BRB-r专家系统的要求。
重构故障传感器观测矩阵的表达式如下:
| $ \hat{\boldsymbol{C}}_{i}\left(\boldsymbol{\rho}_{k}\right)= \sum\limits_{n = 1}^N u \left( {{D_n}} \right) \boldsymbol{\beta}_{n} $ | (22) |
式中:
最后,将重构观测矩阵替换原有观测矩阵,从而实现变体飞行器的容错控制。而对于不可恢复的传感器故障,需要采取切换备份传感器的方式进行容错处理。
2.4 优化模型构建受专家知识不确定性的影响,基于BRB-r的故障诊断与容错控制框架不能准确地对传感器故障进行诊断及容错,需要结合获取的监测数据对专家知识进行调整。传统的P-CMA-ES算法,可以解决高维度、强非线性、多模态的优化问题,能够减少干扰影响,提高全局搜索性能,降低算法的时间复杂度[27]。P-CMA-ES算法在CMA-ES算法的基础上增加了投影算子,使其能够有效地处理BRB-r中的约束问题[28-29]。因此,本文构建了基于P-CMA-ES算法的变体飞行器传感器故障诊断与容错控制优化模型。然后,基于优化模型,选取部分监测数据作为训练数据,同时将剩余数据作为测试数据,以测试优化模型性能。
为保证优化过程中容错控制框架的可解释性,需要对优化参数进行约束。优化目标分为两个:故障诊断的准确度和信息重构的精度。分别建立目标函数为:
| $ {A_c} = \frac{\gamma }{T} $ | (23) |
| $ {\rm{ MSE }} = \frac{1}{T}\sum\limits_{t = 1}^T {{{\left( {{\rm{ output}}{{\rm{ }}_e} - {\rm{ output}}{{\rm{ }}_a}} \right)}^2}} $ | (24) |
式中:Ac为故障诊断的准确度;MSE为信息重构的均方差,用于衡量模型的精度;T为观测数据的个数;γ为诊断准确的个数;outpute、outputa分别为故障传感器观测矩阵的估计输出
模型参数在优化过程中需要遵循以下约束条件:
| $ 0 \leqslant \theta_{k} \leqslant 1, k=1, 2, \cdots, L $ | (25) |
| $ 0 \leqslant \beta_{n, k} \leqslant 1, n=1, \cdots, N, k=1, 2, \cdots, L $ | (26) |
| $ \sum\limits_{n = 1}^N {{\beta _{n, k}}} \le 1, k = 1, 2, \cdots , L $ | (27) |
| $ 0 \leqslant \delta_{i} \leqslant 1, i=1, \cdots, M $ | (28) |
可以看出,在BRB-r专家系统中,属性权重δi、规则权重θk和置信度βn, k是优化参数。对于第k条规则,初始规则权重和初始属性权重由专家给出。如果第k条规则是完整的,输出结果的置信度之和等于1,否则,置信度之和小于1。
3 仿真结果及分析为了验证所提方法的有效性,基于文献[20]中的变体飞行器模型,针对传感器故障诊断与容错控制问题进行仿真验证。由式(5)、(6)可以得到变体飞行器LPV系统的状态空间矩阵为:
| $ {{\boldsymbol{A}}_i}\left( {{\rho _k}} \right) = \left[ {\begin{array}{*{20}{c}} {0.044\;80\rho _k^2 + 0.063\;90{\rho _k} - 2.114\;20}&{1.000\;00}\\ { - 0.623\;40{\rho _k} - 1.985\;40}&{0.035\;91\rho _k^2 + 0.095\;86{\rho _k} - 0.390\;00} \end{array}} \right] $ | (29) |
| $ {{\boldsymbol{B}}_i}\left( {{\rho _k}} \right) = \left[ {\begin{array}{*{20}{c}} {0.000\;03\rho _k^2 + 0.003\;23{\rho _k} + 0.015\;00}\\ {0.831\;70{\rho _k} + 1.406\;90} \end{array}} \right] $ | (30) |
变体飞行器的后掠角变形率ρ随时间t的变化关系为
| $ \left\{\begin{array}{lr} \rho(t)=1.5+1.5 \sin \left(\frac{{\rm{ \mathsf{ π}}}}{35} t-\frac{9}{14} {\rm{ \mathsf{ π}}}\right), & 5 \mathrm{~s} \leqslant t \leqslant 75 \mathrm{~s} \\ \rho(t)=0, & 0 \mathrm{~s}<t<5 \mathrm{~s}, 75 \mathrm{~s}<t<80 \mathrm{~s} \end{array}\right. $ | (31) |
考虑到飞行过程中监测信息受到外界扰动所导致的监测信息不完全可靠以及传感器故障的影响,在文献[20]实现飞行器鲁棒稳定跟踪控制基础上,基于BRB-r构建了变体飞行器传感器故障诊断与容错控制模型。为进一步逼近变体飞行器实际飞行环境,在变体飞行器切换LPV控制模型中添加白噪声。
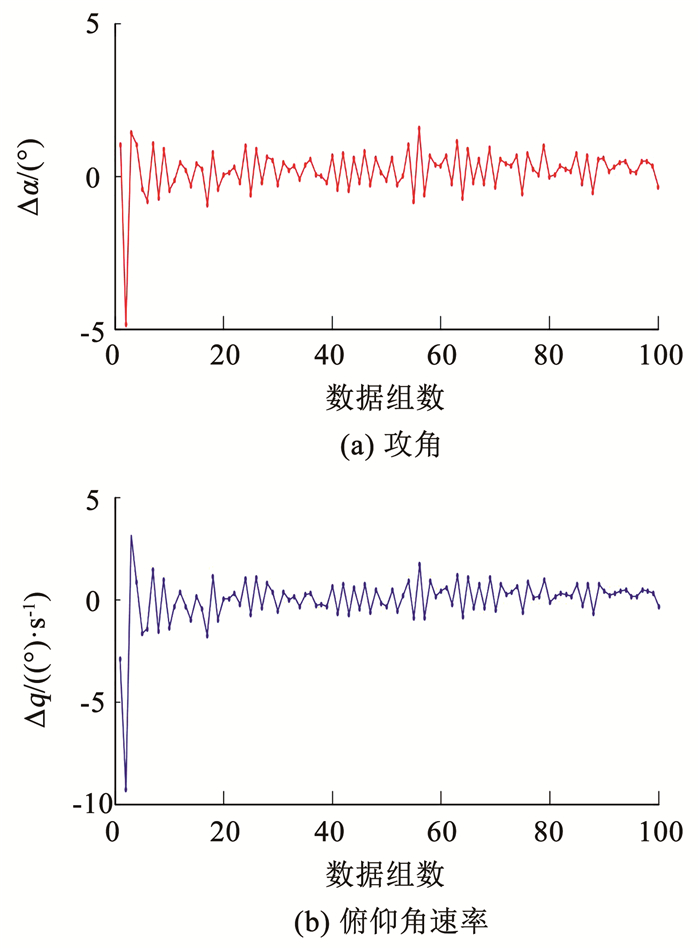
设置传感器部分失效故障的变体飞行器LPV模型的观测矩阵为Ci(ρk)=I2×2,附加干扰信号为d(k)=0.1sin(0.5π),附加矩阵为Di(ρ)=[0.3 0.4]T。变体飞行器正常状态下观测输出如图 3所示。
|
图 3 变体飞行器正常状态下观测输出 Fig. 3 Observation output of morphing aircraft in normal state |
由图 3可以看出,当传感器不发生故障,变体飞行器在飞行过程中仅存在外界扰动的情况下,飞行器系统状态较为稳定,具有良好的稳定飞行性能。结合实验过程所获取的监测数据数量和范围,设定变体飞行器输出状态yi,即攻角和俯仰角速率的参考等级均为7,分别为低(L)、较低(SSL)、稍低(SL)、中等(M)、稍高(SH)、较高(SSH)和高(H)。变体飞行器输出状态的参考等级和参考值见表 1。在变体飞行器观测矩阵重构模型中,对系统状态设置4个参考等级,分别为低(L)、中等(M)、稍高(SH)和高(H),其参考等级和参考值见表 2。
| 表 1 变体飞行器输出状态参考等级和参考值 Tab. 1 Reference level and reference value of output state of morphing aircraft |
| 表 2 观测矩阵重构监测指标参考等级和参考值 Tab. 2 Reference level and reference value of observation matrix reconstruction monitoring index |
对于基于BRB-r专家系统的故障诊断模型,设置4种传感器故障状态,传感器失效故障率分别为0、30%、60%、90%,设置对应的标准故障矩阵为
| $ \boldsymbol{C}=\left[\begin{array}{llll} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array}\right] $ | (32) |
假设两个系统状态同等重要,则指标权重δi=1,根据BRB-r专家系统中规则的构造方式,故障诊断模型中共有49条规则,得到变体飞行器观测器初始故障诊断模型见表 3。观测矩阵重构模型中共有16条规则,得到变体飞行器传感器观测矩阵初始重构模型见表 4。重构后的观测矩阵
| 表 3 变体飞行器观测器初始故障诊断模型 Tab. 3 Initial fault diagnosis model of morphing aircraft observer |
| 表 4 变体飞行器传感器观测矩阵初始重构模型 Tab. 4 Initial reconstruction model of observation matrix for morphing aircraft sensor |
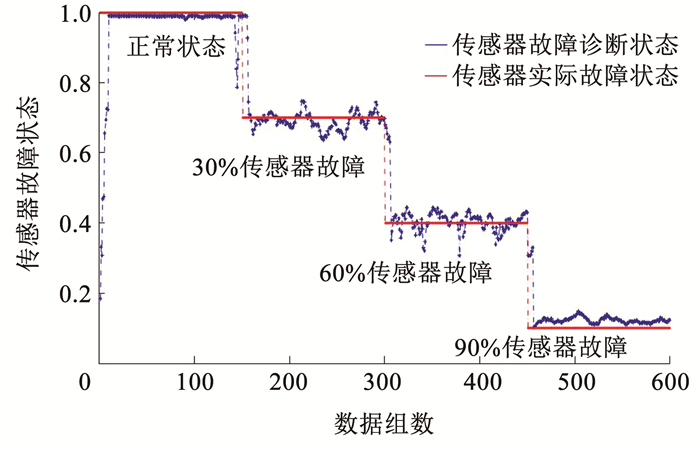
在实验过程中,共计采集1 200组数据。随机选取600组数据作为模型的训练数据,对基于BRB-r专家系统的故障诊断与容错控制模型进行优化训练,其中传感器正常状态、30%故障状态、60%故障状态、90%故障状态均为150组。剩余600组数据作为测试数据,用以测试优化模型性能。在后续测试过程中,将训练数据作为历史信息,测试数据作为在线监测信息,利用历史数据对模型进行训练,并通过在线监测数据对模型参数和结构进行自适应调整[11],迭代次数设置为200次。优化后的传感器故障诊断模型见表 5,优化后的变体飞行器传感器观测矩阵重构模型见表 6,变体飞行器传感器故障诊断结果如图 4所示。
| 表 5 优化后的变体飞行器传感器故障诊断模型 Tab. 5 Fault diagnosis model for morphing aircraft sensor after optimization |
| 表 6 优化后的变体飞行器传感器观测矩阵重构模型 Tab. 6 Reconstruction model of observation matrix for morphing aircraft sensor after optimization |
|
图 4 变体飞行器传感器故障诊断结果 Fig. 4 Results of fault diagnosis for morphing aircraft sensor |
可以看出,对于传感器不同的故障程度,所构建的变体飞行器传感器故障诊断模型能够对其进行准确诊断,总体诊断精度达到了98.75%,这表明故障诊断模型具有较强的鲁棒性能,能够准确诊断传感器故障状态。
在对变体飞行器传感器故障诊断后,需要对变体飞行器LPV切换控制模型中的观测矩阵进行重构,然后将重构后的观测矩阵作为正常观测矩阵传递到变体飞行器LPV控制模型中,从而实现飞行器的稳定飞行控制。为了验证所提控制方法对于飞行器传感器故障的容错控制能力,开展针对不同故障程度的传感器观测矩阵容错控制效果的研究。传感器故障程度分别设置为10%、20%、30%、40%、50%、60%,每种故障程度下重复开展实验200次,不同故障程度的容错控制效果如图 5~10所示。

|
图 5 变体飞行器10%传感器故障容错控制效果 Fig. 5 Fault-tolerant control effect for 10% fault of morphing aircraft sensor |
|
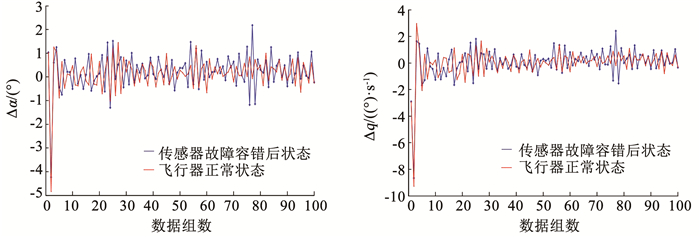
图 6 变体飞行器传感器20%故障容错控制效果 Fig. 6 Fault-tolerant control effect for 20% fault of morphing aircraft sensor |

|
图 7 变体飞行器传感器30%故障容错控制效果 Fig. 7 Fault-tolerant control effect for 30% fault of morphing aircraft sensor |
|
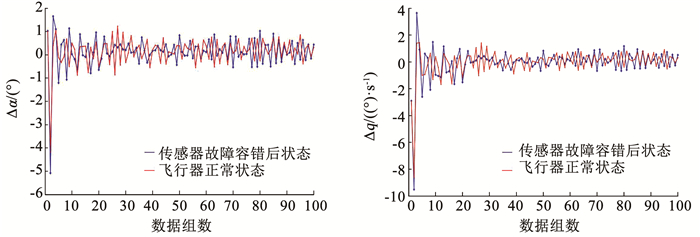
图 8 变体飞行器传感器40%故障容错控制效果 Fig. 8 Fault-tolerant control effect for 40% fault of morphing aircraft sensor |

|
图 9 变体飞行器传感器50%故障容错控制效果 Fig. 9 Fault-tolerant control effect for 50% fault of morphing aircraft sensor |
|
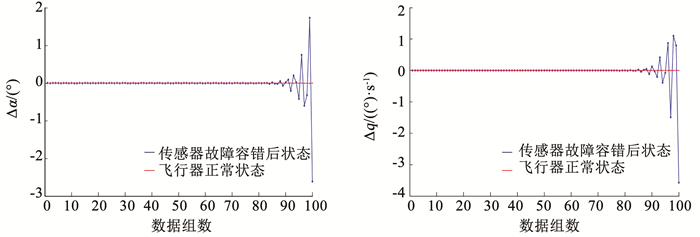
图 10 变体飞行器传感器60%故障容错控制效果 Fig. 10 Fault-tolerant control effect for 60% fault of morphing aircraft sensor |
仿真结果表明,当变体飞行器传感器故障程度≤50%时,可以通过重构观测矩阵,实现飞行器的稳定飞行,容错控制效果良好。当传感器故障≥60%时,该容错控制方法无法实现飞行器的稳定控制。也就是说,当传感器故障程度≥60%时,超出了容错控制能力范围,只能采取切换备份传感器的方式对所发生的故障进行容错,以保证变体飞行器飞行过程中的稳定性能。
通过与仅存在外部干扰情况下的变体飞行器进行对比实验可知:传感器在稳定环境下工作时,其监测信息仅受外部干扰的影响,监测数据在某个值附近呈现均匀、微小波动,变体飞行器LPV控制模型对微小干扰、噪声等具备一定的鲁棒性,能够保证飞行器的稳定性。当存在传感器故障时,监测数据会在其原有基础上发生较大波动,进而导致监测信息攻角和俯仰角速度波动增强。因此,需要基于BRB-r专家系统构建故障诊断模型和容错控制模型,同时利用基于统计方法的可靠性分析和基于P-CMA-ES算法的优化处理,提高了故障诊断精度,而后通过容错控制方法,实现变体飞行器的稳定飞行,并保证良好的跟踪效果。
4 结论1) 构建基于BRB-r专家系统的故障诊断与容错控制框架,利用ER解析算法融合监测数据和专家知识,并通过可靠度分析解决监测数据不完全可靠问题,提高了故障诊断的准确度和容错控制效果。
2) 利用P-CMA-ES算法构建变体飞行器故障诊断与容错控制优化模型,对模型参数进行优化训练,降低模型的复杂度,提高故障诊断与容错控制的效率。
3) 通过MATLAB软件进行仿真验证,结果表明,当变体飞行器传感器发生故障时,该方法仍能使飞行器稳定飞行,具有良好的跟踪效果和较强的鲁棒性能。
| [1] |
CHU Lingling, LI Qi, GU Feng, et al. Design, modeling, and control of morphing aircraft: A review[J]. Chinese Journal of Aeronautics, 2022, 35(5): 220. DOI:10.1016/j.cja.2021.09.013 |
| [2] |
AJAJ R M, PARANCHEERIVILAKKATHIL M S, AMOOZGAR M, et al. Recent developments in the aeroelasticity of morphing aircraft[J]. Progress in Aerospace Sciences, 2021, 120: 100682. DOI:10.1016/j.paerosci.2020.100682 |
| [3] |
王云飞, 肖洪, 杨广, 等. 平行连杆式变形翼结构设计及分布式驱动配置[J]. 哈尔滨工业大学学报, 2022, 54(1): 65. WANG Yunfei, XIAO Hong, YANG Guang, et al. Structure design and distributed actuators configuration of a parallel linkage morphing wing[J]. Journal of Harbin Institute of Technology, 2022, 54(1): 65. DOI:10.11918/202011032 |
| [4] |
BISHAY P L, BURG E, AKINWUNMI A, et al. Development of a new span-morphing wing core design[J]. Designs, 2019, 3(1): 12. DOI:10.3390/designs3010012 |
| [5] |
YUE Ting, ZHANG Xiangyang, WANG Lixin, et al. Flight dynamic modeling and control for a telescopic wing morphing aircraft via asymmetric wing morphing[J]. Aerospace Science and Technology, 2017, 70: 328. DOI:10.1016/j.ast.2017.08.013 |
| [6] |
AJAJ R M, BEAVERSTOCK C S, FRISWELL M I. Morphing aircraft: The need for a new design philosophy[J]. Aerospace Science and Technology, 2016, 49: 154. DOI:10.1016/j.ast.2015.11.039 |
| [7] |
LI Daochun, ZHAO Shiwei, DA RONCH A, et al. A review of modelling and analysis of morphing wings[J]. Progress in Aerospace Sciences, 2018, 100: 46. DOI:10.1016/j.paerosci.2018.06.002 |
| [8] |
TSUSHIMA N, TAMAYAMA M. Recent researches on morphing aircraft technologies in Japan and other countries[J]. Mechanical Engineering Reviews, 2019, 6(2): 19. DOI:10.1299/mer.19-00197 |
| [9] |
LIVNE E. Aircraft active flutter suppression: State of the art and technology maturation needs[J]. Journal of Aircraft, 2018, 55(1): 410. DOI:10.2514/1.c034442 |
| [10] |
VASISTA S, TONG Liyong, WONG K C. Realization of morphing wings: A multidisciplinary challenge[J]. Journal of Aircraft, 2012, 49(1): 11. DOI:10.2514/1.c031060 |
| [11] |
胡昌华, 周志杰, 冯志超. 一种复杂传感器网络自适应动态故障诊断方法及系统: CN112116003A[P]. 2020-12-22 HU Changhua, ZHOU Zhjie, FENG Zhichao. An adaptive dynamic fault diagnosis method and system for complex sensor networks: CN112116003A[P]. 2020-12-22 |
| [12] |
TAIMOOR M, LI Aijun. Lyapunov theory based adaptive neural observers design for aircraft sensors fault detection and isolation[J]. Journal of Intelligent & Robotic Systems, 2020, 98(2): 311. DOI:10.1007/s10846-019-01098-8 |
| [13] |
MENON A, RAFI M, SCHIRMER G, et al. Measurement of wing deflections in flexible aircraft using the sansec smart sensor[J]. IEEE Aerospace and Electronic Systems Magazine, 2017, 32(10): 14. DOI:10.1109/MAES.2017.160133 |
| [14] |
ANSARI A, BERNSTEIN D S. Aircraft sensor fault detection using state and input estimation[C]//2016 American Control Conference(ACC). Boston, MA: IEEE Press, 2016: 5951. DOI: 10.1109/ACC.2016.7526603
|
| [15] |
HEREDIA G, OLLERO A. Virtual sensor for failure detection, identification and recovery in the transition phase of a morphing aircraft[J]. Sensors, 2010, 10(3): 2188. DOI:10.3390/s100302188 |
| [16] |
CARTOCCI N, COSTANTE G, NAPOLITANO M R, et al. PCA methods and evidence based filtering for robust aircraft sensor fault diagnosis[C]//2020 28th Mediterranean Conference on Control and Automation(MED). Saint-Raphaël, France: IEEE, 2020: 550. DOI: 10.1109/MED48518.2020.9182973
|
| [17] |
AOUAOUDA S, CHADLI M. Model reference tracking control for uncertain Takagi-Sugeno systems subject to sensor faults[J]. IFAC-PapersOnline, 2015, 48(21): 1250. DOI:10.1016/j.ifacol.2015.09.697 |
| [18] |
RABAOUI B, HAMDI H, BENHADJ BRAIEK N. An adaptive polytopic observer-based sensor fault tolerant controller design[C]//2018 International Conference on Advanced Systems and Electric Technologies(IC-ASET). Hammamet, Tunisia: IEEE, 2018: 174. DOI: 10.1109/ASET.2018.8379854
|
| [19] |
TAIMOOR M, LI Aijun. Neural-sliding mode approach-based adaptive estimation, isolation and tolerance of aircraft sensor fault[J]. Aircraft Engineering and Aerospace Technology, 2020, 92(2): 237. DOI:10.1108/AEAT-05-2019-0106 |
| [20] |
夏川, 董朝阳, 程昊宇, 等. 变体飞行器有限时间切换H∞跟踪控制[J]. 兵工学报, 2018, 39(3): 485. XIA Chuan, DONG Chaoyang, CHENG Haoyu, et al. Finite-time H∞ tracking control for switched morphing aircraft[J]. Acta Armamentarii, 2018, 39(3): 485. DOI:10.3969/j.issn.1000-1093.2018.03.010 |
| [21] |
YANG Jianbo, LIU Jun, WANG Jin, et al. Belief rule-base inference methodology using the evidential reasoning approach-RIMER[J]. IEEE Transactions on Systems, Man, and Cybernetics-Part A: Systems and Humans, 2006, 36(2): 266. DOI:10.1109/TSMCA.2005.851270 |
| [22] |
ZHOU Zhijie, HU Guanyu, HU Changhua, et al. A survey of belief rule-base expert system[J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2021, 51(8): 4944. DOI:10.1109/TSMC.2019.2944893 |
| [23] |
FENG Zhichao, ZHOU Zhijie, HU Changhua, et al. A new belief rule base model with attribute reliability[J]. IEEE Transactions on Fuzzy Systems, 2019, 27(5): 903. DOI:10.1109/TFUZZ.2018.2878196 |
| [24] |
ZHOU Zhijie, FENG Zhichao, HU Changhua, et al. Aeronautical relay health state assessment model based on belief rule base with attribute reliability[J]. Knowledge-Based Systems, 2020, 197: 105869. DOI:10.1016/j.knosys.2020.105869 |
| [25] |
冯志超, 周志杰, 胡昌华, 等. 存在环境干扰下航天继电器故障诊断与容错控制方法[J]. 中国科学: 信息科学, 2021, 51(4): 648. FENG Zhichao, ZHOU Zhijie, HU Changhua, et al. A fault diagnosis and tolerant control method for aerospace relay with environmental disturbance[J]. Scientia Sinica Informationis, 2021, 51(4): 648. DOI:10.1360/SSI-2020-0189 |
| [26] |
FENG Zhichao, HE Wei, ZHOU Zhijie, et al. A new safety assessment method based on belief rule base with attribute reliability[J]. IEEE/CAA Journal of Automatica Sinica, 2021, 8(11): 1774. DOI:10.1109/JAS.2020.1003399 |
| [27] |
HANSEN N, MVLLER S D, KOUMOUTSAKOS P. Reducing the time complexity of the derandomized evolution strategy with covariance matrix adaptation(CAM-ES)[J]. Evolutionary Computation, 2003, 11(1): 1. DOI:10.1162/106365603321828970 |
| [28] |
HU Guanyu, ZHOU Zhijie, HU Changhua, et al. Hidden behavior prediction of complex system based on time-delay belief rule base forecasting model[J]. Knowledge-Based Systems, 2020, 203: 106147. DOI:10.1016/j.knosys.2020.106147 |
| [29] |
SUN Chao, YANG Ruohan, HE Wei, et al. A novel belief rule base expert system with interval-valued references[J]. Scientific Reports, 2022, 12: 6786. DOI:10.1038/s41598-022-10636-8 |
 2023, Vol. 55
2023, Vol. 55


