电力负荷预测的研究始于20世纪60年代,统计方法是最早提出的方法,主要有时间序列法[1]、回归法[2]和指数平滑法[3],但这些模型相对简单,不能满足非线性时间序列的要求。随着分布式电源[4]和智能设备在智能电网环境中的广泛应用,负荷数据规模急剧增加,呈现出更复杂的变化规律和特征[5],神经网络开始取代传统方法。Zheng等[6]采用典型的BP神经网络进行负荷预测,但BP神经网络结构简单,泛化能力差,容易陷入局部最优,预测精度不高。为克服这一局限性,研究人员开始尝试将单个神经网络与其他算法相结合,并取得了一定的成果。Gensler等[7]将自动编码器和LSTM相结合对可再生能源发电厂进行预测。Han等[8]将具有k均值聚类的卷积神经网络(Convolutional neural network, CNN)应用于短期预测。但是简单的LSTM网络与CNN网络在长时间序列或多维输入数据面前,仍然存在序列特征信息丢失、数据间结构信息紊乱、多维特征挖掘不够充分等问题。Shi等[9]使用汇集深度递归神经网络(Pooling-based deep recurrent neural network, PDRNN),提出向神经网络添加更多层可以提高预测性能。Pan等[10]提出了深度信念网络(Deep belief network, DBN)算法,通过使用集成方法和支持向量回归(Support vector regression, SVR)提高DBN的负荷预测性能,但DBN在计算过程中存在着训练时间较长、容易过拟合的缺点。
本文基于深度学习方法中经典LSTM神经网络在负荷预测中的应用成果,采用加入注意力机制的双向LSTM结构,并将其与改进的深度残差网络结合,提出一种混合网络模型—残差AM-Bi-LSTM预测模型。通过增加捷径连接和改变捷径连接方式,从时间、特征维度和网络深度3个方面提升模型的预测精度和泛化能力。
1 残差AM-Bi-LSTM预测模型 1.1 Bi-LSTM网络一个LSTM单元包括输入门、遗忘门和输出门,如图 1所示。这些门结构使LSTM在进行反向传播时能够保持更稳定的误差,使神经网络可以在多个时间步上继续学习[11]。

|
图 1 LSTM单元的内部结构 Fig. 1 Internal structure of an LSTM cell |
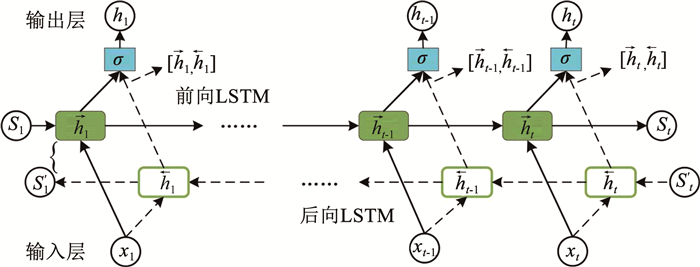
通常,LSTM网络中的信息是单向传输的,LSTM只能使用过去的信息,不能使用未来的信息。Bi-LSTM包含前向LSTM层和后向LSTM层[12],可以对输入的电力负荷序列数据进行双向时序特征提取。其网络结构如图 2所示,图中
| $ \overrightarrow{\boldsymbol{h}}_{t}=\overrightarrow{\operatorname{LSTM}}\left(\overrightarrow{\boldsymbol{h}}_{t-1}, \boldsymbol{x}_{t}, \vec{C}_{t-1}\right), t \in[1, T] $ | (1) |
| $ \overleftarrow{\boldsymbol{h}}_{t}=\overleftarrow{\operatorname{LSTM}}\left(\overleftarrow{\boldsymbol{h}}_{t+1}, \boldsymbol{x}_{t}, \overleftarrow{C}_{t+1}\right), t \in[T, 1] $ | (2) |
| $ \boldsymbol{h}_{t}=\sigma\left(\boldsymbol{W}_{h}\left[\overrightarrow{\boldsymbol{h}}_{t}, \overleftarrow{\boldsymbol{h}}_{t}\right]+\boldsymbol{b}_{h}\right) $ | (3) |
|
图 2 Bi-LSTM模型结构 Fig. 2 Bi-LSTM network structure |
式中:xt为t时刻的输入值,
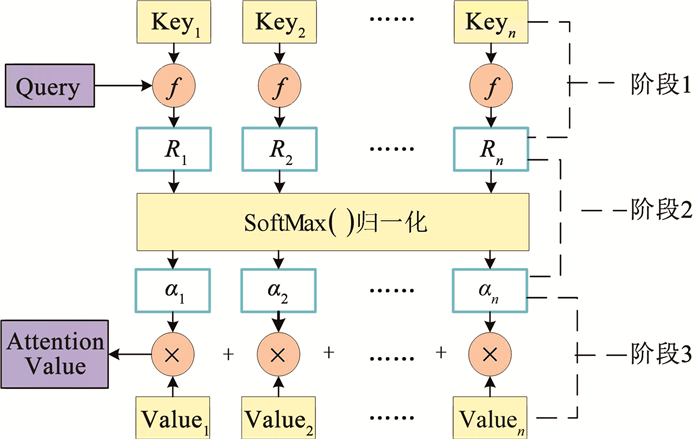
注意力机制[13]源于模仿人类大脑的注意力特性。注意力机制的核心思想是将关注的重点放在对输出有重要影响的输入序列的重要环节,而较少地关注输入序列的其他信息,这样就可以巧妙、合理地改变对外界信息的注意力,放大所需信息,忽略无关信息。因此,信息的接收灵敏度和处理速度大大提高。注意力机制的实现过程如图 3所示。
|
图 3 注意力机制计算过程 Fig. 3 Three stages of calculation of attention value |
深度残差网络[14]是2015年提出的一种具有重要意义的网络结构。在神经网络中,通常通过增加网络层数来提高模型的精度,但受梯度消失与梯度爆炸的影响,深层网络的实际表现可能比浅层网络更差。深度残差网络中,通过残差网络上的短接路径,梯度可以在非常深的网络中连贯的传播而不受到过多卷积层梯度的叠加,这从本质上避免了梯度消失与梯度爆炸问题。深度残差网络一般通过堆叠多个残差块构成,残差块结构与深度残差网络如图 4(a)、(b)所示。

|
图 4 残差块、深度残差网络与ResNetPlus网络结构 Fig. 4 Structure of residual block, depth residual network and ResNetPlus network |
残差网络的优异性能主要得益于它的捷径连接。利用恒等映射捷径连接的一个残差块的输出可以用如下公式表示:
| $ \boldsymbol{x}_{l+1}=F\left(\boldsymbol{x}_{l}, \boldsymbol{w}_{l}\right)+\boldsymbol{x}_{l} $ | (4) |
式中:xl、xl+1分别为残差网络中第l个残差块的输入和输出,F为要学习的残差映射,wl为要学习的权重参数。
如果堆叠了K个残差块,则结构的正向传播可以表示为
| $ \boldsymbol{x}_{K}=\boldsymbol{x}_{0}+\sum\limits_{i=1}^{K} F\left(\boldsymbol{x}_{i-1}, \boldsymbol{W}_{i-1}\right) $ | (5) |
式中:x0为残差网络的输入,xK为第K个残差块的输出,Wi={wi, l|1≤l≤L} 为与第i个残差块关联的权重集,L为残差块内的层数。式(5)说明了残差网络的前向传播过程,即数据如何从残差网络的浅层1传递到深层K的学习过程。误差的反向传播可以表示为
| $ \begin{gathered} \frac{\partial \operatorname{loss}}{\partial \boldsymbol{x}_{0}}=\frac{\partial \operatorname{loss}}{\partial \boldsymbol{x}_{K}} \cdot \frac{\partial \boldsymbol{x}_{K}}{\partial \boldsymbol{x}_{0}}= \\ \frac{\partial \operatorname{loss}}{\partial \boldsymbol{x}_{K}} \cdot\left(1+\frac{\partial}{\partial \boldsymbol{x}_{0}} \sum\limits_{i=1}^{K} F\left(\boldsymbol{x}_{i-1}, \boldsymbol{W}_{i-1}\right)\right) \end{gathered} $ | (6) |
式中: loss为神经网络的损失函数,“1”为残差网络中的捷径连接。
Chen等[15]改进了常规意义上的残差网络架构,给出了一种新的深度残差网络的变体,并命名为ResNetPlus。如图 4(c)所示,与传统的残差网络结构不同,模型的每一层由主残差块和侧残差块两个残差块构成。改进的深度残差网络由于加入了更多的残差块和捷径连接,大大提升了网络误差的反向传播效率。
1.4 残差AM-Bi-LSTM负荷预测模型残差AM-Bi-LSTM组合预测模型由输入层、ResNetPlus层和AM-Bi-LSTM层组成。模型使用ResNetPlus层来提取输入数据的隐藏特征,生成特征向量并整合为一个已编码特征输入到AM-Bi-LSTM层。最后,通过AM-Bi-LSTM层整合数据样本与数据特征,输出最终预测值。残差AM-Bi-LSTM模型结构如图 5所示。

|
图 5 残差AM-Bi-LSTM模型结构图 Fig. 5 Structure of residual AM-Bi-LSTM model |
本文的测试基于ISO-NE数据集。ISO-NE数据集对2003—2014年间美国某地区的4 324 d的每小时负荷数据进行了统计,总计103 776条。数据集的划分方式见表 1,将2003年5月—2005年12月的每小时负荷数据作为训练集,并将其后一年的负荷数据作为测试集。
| 表 1 数据集划分方式 Tab. 1 Data set division method |
负荷数据在模型训练过程中占主要地位,由于负荷数据具有很大的数量级,若不对数据进行归一化处理,模型很难正确收敛到最优解。本文采用极值法对收集的电力负荷数据及温度数据进行批量归一化处理,即
| $ Y^{\prime}=\frac{Y-Y_{\text {min }}}{Y_{\text {max }}-Y_{\text {min }}} $ | (7) |
式中:Y′为归一化后的负荷或温度数据,Y为原始负荷或温度数据,Ymin为负荷或温度数据中的最小值,Ymax为负荷或温度数据中的最大值。以训练集前10 d数据为例,归一化后的负荷与温度数据曲线如图 6所示。

|
图 6 归一化后的负荷与温度曲线 Fig. 6 Normalized load and temperature curve |
数据经归一化后就可划分为训练集和测试集并将其输入到模型中进行训练与预测,最后还需要对得到的预测值进行反归一化[16],即
| $ \hat{Y}=\left(Y_{\text {max }}-Y_{\text {min }}\right) Y_{\text {pred }}+Y_{\text {min }} $ | (8) |
式中:
表 2列出了用于预测第2天第h小时负荷Lh的输入。
| 表 2 基础结构模型输入 Tab. 2 Basic structure model input |
为捕捉负荷、温度和时间序列的短期接近度和周期性趋势,选择Lhmonth、Lhweek、Thmonth和Thweek(选择与预测日相同的星期数的日期,因为它们更有可能具有相似的负荷特征)以及Lhday和Thday作为网络输入。输入Lhhour将最近24 h的负荷提供给模型。此外,还为季节、工作日与非工作日和节假日与非节假日分别添加了一个one-hot编码,以便让模型能够更加顺利地获取历史负荷时间序列的周期性和非常规时间特征[17]。最后将1 h预测模型的输出作为模型第2部分残差AM-Bi-LSTM网络的输入。
3 结果与分析 3.1 多模型集成策略本文在模型中应用了Snapshot集成方法,在一次模型训练过程中截取4个Snapshot点,如图 7所示。

|
图 7 Snapshot集成策略 Fig. 7 Snapshot integration strategy |
每一个Snapshot点是在适当的迭代次数之后截取的,因此每个Snapshot点的损失程度相似。在获得所有Snapshot点的模型后,本文对模型的输出进行平均,并生成最终预测。
3.2 预测结果评价指标为评价预测模型的性能,通常选用均方根误差(RMSE)和平均绝对误差百分比(MAPE)为评价预测模型准确率的评价指标[18]。计算公式为:
| $ \mathrm{RMSE} =\sqrt{\frac{\sum\limits_{t=1}^{n}\left(f(x)_{t}-y_{t}\right)^{2}}{n}} $ | (9) |
| $ \mathrm{MAPE} =\frac{1}{n} \sum\limits_{t=1}^{n}\left|\frac{f(x)_{t}-y_{t}}{y_{t}}\right| \times 100 $ | (10) |
式中:yt为t时刻的实际值,f(x)t为t时刻的预测值,n为观测次数。
3.3 不同网络深度的模型预测结果对比分析本文对比测试了不同网络深度下常规LSTM模型[19]和残差AM-Bi-LSTM模型的预测性能,测试结果见表 3。未使用残差网络的常规LSTM网络在层级增大到一定程度时,其预测误差表现出了明显的上升的趋势,而残差AM-Bi-LSTM模型的精度随着LSTM的层数增加而不断提升。图 8显示了LSTM层数为16层时两模型的MAPE曲线。16层的残差AM-Bi-LSTM模型的MAPE仅为1.73%,约为具有相同层数的常规LSTM网络MAPE的1/3,这是因为引入的残差网络在前向传播时,网络中的恒等映射可将输入信号从任意底层直接传到高层,一定程度上解决了网络退化问题。
| 表 3 不同网络深度下模型性能对比 Tab. 3 Comparison of model performance under different network depths |

|
图 8 16层模型性能对比 Fig. 8 Comparison of 16 layers model performance |
本文将所提的残差AM-Bi-LSTM网络模型与目前多种主流深度学习模型的预测结果进行对比测试,测试结果如表 4和图 9所示。与单纯采用残差网络或AM-Bi-LSTM网络相比,本文提出的组合模型在很大程度上减少了系统的学习错误,且残差AM-Bi- LSTM模型的MAPE仅为传统LSTM网络的1/3。
| 表 4 残差AM-Bi-LSTM模型与主流模型性能对比 Tab. 4 Performance comparison among residual AM-Bi-LSTM model and conventional models |

|
图 9 不同网络模型的预测误差对比 Fig. 9 Comparison of predicted errors of different network models |
本文对比了残差AM-Bi-LSTM模型、AM-Bi-LSTM模型和ResNetPlus模型在不同年份的预测结果,结果如图 10所示,进一步验证了本文所提模型具有较高的预测精度和泛化能力。

|
图 10 不同模型在不同年份上的预测结果 Fig. 10 Predicted results of different models in different years |
由图 10可以看出,相较于AM-Bi-LSTM模型和ResNetPlus模型,在3 a的预测结果中,残差AM-Bi-LSTM模型在预测精度上均有1.00%左右的提高。在对不同年份的预测结果中,残差AM-Bi-LSTM网络模型的预测准确率变化较小,说明采用集成方法可以保证模型具有一定的鲁棒性。
LSTM模型和残差AM-Bi-LSTM模型对不同月份的预测结果如图 11所示,预测曲线如图 12(选取每个季度的第1个月为例)所示。相较于LSTM模型,残差AM-Bi-LSTM模型在每个月份上均拥有更低的MAPE且波动更小。

|
图 11 不同模型的每月预测结果对比 Fig. 11 Comparison of monthly predicted results of different models |

|
图 12 不同模型不同月份预测曲线 Fig. 12 Forecast curve of different models in different months |
根据图 11数据,12个月内LSTM模型的MAPE为4.66%,残差AM-Bi-LSTM模型的MAPE为1.79%,将预测精度的平均值提升了2.87%。另一方面,由于大多数超参数没有在ISO-NE数据集上进行调整,可以得出该模型具有良好的泛化能力。
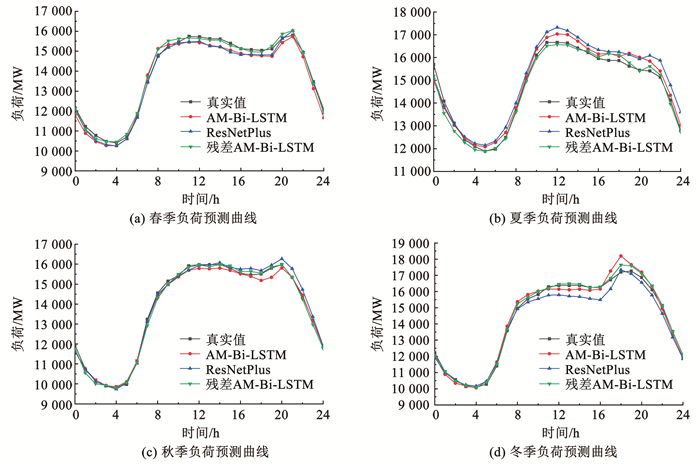
表 5为不同模型在不同季节下预测结果的MAPE对比(在每个季节最中间的两星期随机选取3 d为例),图 13显示了残差AM-Bi-LSTM网络模型、AM-Bi-LSTM模型以及ResNetPlus模型在不同季节上的预测曲线。
| 表 5 不同模型在不同季节上的预测结果(MAPE) Tab. 5 Predicted results of different models in different seasons (MAPE) |
|
图 13 不同模型在不同季节的预测结果 Fig. 13 Predicted results of different models in different seasons |
从图 13中可以看出,相比于AM-Bi-LSTM和ResNetPlus两个模型,残差AM-Bi-LSTM模型在4个季节中得到的预测曲线都是最接近实际负荷值的。以平均绝对百分比误差MAPE作为主要评价指标,对比3种模型在4个季节上的平均预测结果(见表 5),残差AM-Bi-LSTM模型的MAPE为1.81%。AM-Bi-LSTM和ResNetPlus模型的MAPE分别为2.86%和2.97%,预测误差分别比残差AM-Bi-LSTM模型高出1.05%和1.16%。此外,由图 13(b)、(d)可知,ResNetPlus模型的夏季和冬季负荷预测曲线和真实值有较大的偏差,说明ResNetPlus模型对时间特征的提取较差,而残差AM-Bi-LSTM模型的4个季节的预测精度没有较大波动,表明所提模型在不同的季节中都能较准确地对负荷进行预测,具有较高的稳定性和泛化能力。
4 结论1) 本文所提模型结合了注意力机制、多层改进残差网络和Bi-LSTM网络,并采用Snapshot集成策略,从深度、特征提取、时间、稳定性等多方面提升模型的性能。
2) 与LSTM和AM-Bi-LSTM模型相比,所提模型在相同条件下的平均预测精度分别提升2.87%和1.05%,说明引入改进深度残差网络能有效提高负荷预测的精度。
3) 与ResNetPlus模型相比,所提模型在不同季节负荷预测的平均预测精度提升了1.16%,并且预测精度不被季节变化影响,说明所提模型能够充分提取输入数据的时间特征,有较强的准确率、鲁棒性以及泛化能力。
| [1] |
DORDONNAT V, PICHAVANT A, PIERROT A. GEFCom2014 probabilistic electric load forecasting using time series and semi-parametric regression models[J]. International Journal of Forecasting, 2016, 32(3): 1005. DOI:10.1016/j.ijforecast.2015.11.010 |
| [2] |
LUO Jian, HONG Tao, FANG S C. Robust regression models for load forecasting[J]. IEEE Transactions on Smart Grid, 2019, 10(5): 5397. DOI:10.1109/TSG.2018.2881562 |
| [3] |
MI Jianwei, FAN Libin, DUAN Xuechao, et al. Short-term power load forecasting method based on improved exponential smoothing grey model[J]. Mathematical Problems in Engineering, 2018, 2018: 1. DOI:10.1155/2018/3894723 |
| [4] |
梁志峰, 叶畅, 刘子文, 等. 分布式电源集群并网调控: 体系架构与关键技术[J]. 电网技术, 2021, 45(10): 3791. LIANG Zhifeng, YE Chang, LIU Ziwen, et al. Grid-connected scheduling and control of distributed generations clusters: Architecture and key technologies[J]. Power System Technology, 2021, 45(10): 3791. DOI:10.13335/j.1000-3673.pst.2020.2236 |
| [5] |
SYED D, ZAINAB A, GHRAYEB A, et al. Smart grid big data analytics: Survey of technologies, techniques, and applications[J]. IEEE Access, 2020, 9: 59564. DOI:10.1109/ACCESS.2020.3041178 |
| [6] |
ZHENG Xufeng, XIONG Hejin, WEI Di. Short-term load forecasting of BP network based on EMD[C]//2019 IEEE 8th Joint International Information Technology and Artificial Intelligence Conference (ITAIC). Chongqing, China: IEEE, 2019: 1093. DOI: 10.1109/ITAIC.2019.8785641
|
| [7] |
GENSLER A, HENZE J, SICK B, et al. Deep learning for solar power forecasting—an approach using AutoEncoder and LSTM neural networks[C]//2016 IEEE International Conference on Systems, Man, and Cybernetics (SMC). Budapest, Hungary: IEEE, 2017: 2858. DOI: 10.1109/SMC.2016.7844673
|
| [8] |
HAN Fujia, PU Tianjiao, LI Maozhen, et al. Short-term forecasting of individual residential load based on deep learning and K-means clustering[J]. CSEE Journal of Power and Energy Systems, 2020, 7(2): 261. DOI:10.17775/CSEEJPES.2020.04060 |
| [9] |
SHI Heng, XU Minghao, LI Ran. Deep learning for household load forecasting—a novel pooling deep RNN[J]. IEEE Transactions on Smart Grid, 2018, 9(5): 5271. DOI:10.1109/TSG.2017.2686012 |
| [10] |
PAN Yi, ZHENG Jianyong, YANG Yun, et al. An electricity load forecasting approach combining DBN-based deep neural network and NAR model for the integrated energy systems[C]//2019 IEEE International Conference on Big Data and Smart Computing (BigComp). Kyoto, Japan: IEEE, 2019: 1. DOI: 10.1109/BIGCOMP.2019.8679194
|
| [11] |
CUI Can, HE Ming, DI Fangchun, et al. Research on power load forecasting method based on LSTM model[C]//2020 IEEE 5th Information Technology and Mechatronics Engineering Conference (ITOEC). Chongqing, China: IEEE, 2020: 1657. DOI: 10.1109/ITOEC49072.2020.9141684
|
| [12] |
张淑清, 李君, 姜安琦, 等. 基于FPA-VMD和BiLSTM神经网络的新型两阶段短期电力负荷预测[J]. 电网技术, 2022, 46(8): 3269. ZHANG Shuqing, LI Jun, JIANG Anqi, et al. A novel two-stage model based on FPA-VMD and BiLSTM neural network for short-term power load forecasting[J]. Power System Technology, 2022, 46(8): 3269. DOI:10.13335/j.1000-3673.pst.2021.0969 |
| [13] |
彭文, 王金睿, 尹山青. 电力市场中基于Attention-LSTM的短期负荷预测模型[J]. 电网技术, 2019, 43(5): 1745. PENG Wen, WANG Jinrui, YIN Shanqing. Short-term load forecasting model based on attention-LSTM in electricity market[J]. Power System Technology, 2019, 43(5): 1745. DOI:10.13335/j.1000-3673.pst.2018.1554 |
| [14] |
GAO Zheng, TONG Lei, ZHOU Jun, et al. Stochastic depth residual network for hyperspectral image classification[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 1. DOI:10.1109/TGRS.2021.3090429 |
| [15] |
CHEN Kunjin, CHEN Kunlong, WANG Qin, et al. Short-term load forecasting with deep residual networks[J]. IEEE Transactions on Smart Grid, 2019, 10(4): 3943. DOI:10.1109/TSG.2018.2844307 |
| [16] |
WANG Yizhen, ZHANG Ningqing, CHEN Xiong. A short-term residential load forecasting model based on LSTM recurrent neural network considering weather features[J]. Energies, 2021, 14(10): 2737. DOI:10.3390/en14102737 |
| [17] |
杨德昌, 赵肖余, 何绍文, 等. 面向海量用户用电数据的集成负荷预测[J]. 电网技术, 2018, 42(9): 2923. YANG Dechang, ZHAO Xiaoyu, HE Shaowen, et al. Aggregated load forecasting based on massive household smart meter data[J]. Power System Technology, 2018, 42(9): 2923. DOI:10.13335/j.1000-3673.pst.2018.0507 |
| [18] |
周洲, 焦文玲, 任乐梅, 等. 蚁群算法分配权重的燃气日负荷组合预测模型[J]. 哈尔滨工业大学学报, 2021, 53(6): 177. ZHOU Zhou, JIAO Wenling, REN Lemei, et al. Combined forecasting model of gas daily load based on weight distribution of ant colony algorithm[J]. Journal of Harbin Institute of Technology, 2021, 53(6): 177. DOI:10.11918/201911084 |
| [19] |
KO M S, LEE K, KIM J K, et al. Deep concatenated residual network with bidirectional LSTM for one-hour-ahead wind power forecasting[C]//2022 IEEE Power & Energy Society General Meeting(PESGM). Denver, CD: IEEE. 2022: 1. DOI: 10.1109/PESGM48719.2022.9916711
|
 2023, Vol. 55
2023, Vol. 55


