链式输送机是坦克自动装弹机的重要组成部分,是一种结构复杂,工作环境恶劣的机电系统,在使用过程中常出现零部件磨损变形和动力源变化等故障,导致自动装弹机装填性能下降。利用系统运行过程信息进行故障识别能够及时发现此类故障,判断故障发生部位,防止严重失效。
得益于计算机技术与机器学习算法的发展,数据驱动方法在故障识别中得到了广泛应用,其中如何将原始信号转换为敏感特征是一个关键问题。国内、外学者针对连续旋转机械的非平滑振动信号,使用信号分析方法[1-3]进行了大量研究。坦克自动装弹机机电系统不是连续工作的,一般会记录运行过程中诸如位移、速度等时序数据。对于此类系统通常以离散数据的形式采用主成分分析[4]和自动编码器[5]等方法进行特征提取,但忽略了时序数据的平滑特性,因此学者们将视角转向函数型数据分析(Functional data analysis, FDA)。FDA是以函数视角分析时序数据的一种方法,能够将平滑的时序数据视为具有统一结构的连续函数进行信息挖掘[6]。经典的函数型主成分分析(Functional principal component analysis, FPCA)是主成分分析在Hilbert空间的拓展,在故障诊断领域作为特征提取技术得到应用[7-8]。主微分分析(Principal differential analysis, PDA)是FDA中一种简洁的泛函分析方法,通过微分方程反映数据的动态变化特征,主要用于对观测数据的变化过程进行建模[9-10]。而Jang等[11]利用线性微分方程的解集是基础解系张成的线性空间构成的这一原理,将PDA拓展为函数型数据维数约简的另一种方法。但目前还未见PDA在故障诊断中的应用。
复杂机电系统的单一传感器信号不能全面反映系统运行特性,其数据特征往往对部分故障不敏感。多传感器数据特征融合是解决这一问题的有效方法。传统的特征融合技术独立于模式识别算法,通过特定的准则评估特征融合的效果[12-13]。随着深度学习的发展,特征融合与模式识别算法形成一个整体,通过自动编码器的无监督深层特征学习实现特征融合[14-15]。多层极限学习机是一种基于极限学习机自动编码器的深度学习模型[16],保留了极限学习机快速学习的优势,但仍具备极限学习机固有的随机特性。因此Li等[17]提出了基于核极限学习机自动编码器(Kernel extreme learning machine auto-encoder, KELM-AE)的多层核极限学习机(Multi-layer kernel extreme learning machine, ML-KELM),通过对高光谱数据集的分类表明多层核极限学习机具有优异的分类性能。
基于上述分析,本文回顾了基于FPCA的时序数据特征提取方法,同时将PDA引入了故障诊断领域作为特征提取技术。使用Relief-F算法从FPCA和PDA提取的多传感器数据特征中选择与分类强相关的特征,进而采用ML-KELM深度学习框架实现特征融合与分类识别。通过链式输送机故障识别实验初步验证了所提方法的可行性。
1 基于FPCA的时序数据特征提取 1.1 时序数据的函数化使用FDA分析时序数据时首先要将离散数据拟合为函数。设第i(i=1, 2, …, N)个观测样本为{(yij, tj)|j=1, 2, …, n},可表示为yij=xi(tj)+eij,其中xi(tj)为tj时刻函数xi(t)的函数值,eij为相应的拟合误差。使用基函数展开法将xi(t)表示为
| $ x_{i}(t)=\sum\limits_{u=1}^{U} c_{i u} \phi_{u}(t)=\boldsymbol{c}_{i}^{\mathrm{T}} \boldsymbol{\phi} $ | (1) |
式中:ci=[ci1, ci2, …, ciU]T为基函数的系数向量,ϕi=[ϕ1(t), ϕ2(t), …, ϕU(t)]T为U个基函数组成的函数型向量,本文选用适用于非周期数据的B样条基函数,具有良好的可导性和局部性。
利用加权最小二乘准则最小化误差平方和估计系数向量ci。求解时基函数个数越大,数据拟合度越好,但函数平滑性越差。为了兼顾数据拟合度和函数平滑性,引入a阶粗糙度惩罚函数:
| $ l_{a}\left(x_{i}(t)\right)=\int\left[D^{a} x_{i}(t)\right]^{2} \mathrm{~d} t=\boldsymbol{c}_{i}^{\mathrm{T}} \boldsymbol{J} \boldsymbol{c}_{i} $ | (2) |
式中:Da为a阶微分算子,J=∫DaϕDaϕTdt。
估计系数向量ci的加权最小二乘准则为
| $ \min\limits _{\boldsymbol{c}_{i}}\left(\boldsymbol{y}_{i}-\boldsymbol{\varPhi} \boldsymbol{c}_{i}\right)^{\mathrm{T}} \boldsymbol{W}\left(\boldsymbol{y}_{i}-\boldsymbol{\varPhi} \boldsymbol{c}_{i}\right)+\lambda \boldsymbol{c}_{i}^{\mathrm{T}} \boldsymbol{J} \boldsymbol{c}_{i} $ | (3) |
式中:yi为观测样本的向量形式,Φ为ϕu(tij) 组成的n×U阶矩阵,W为加权矩阵,λ为平滑参数。
系数向量ci的估计值为
| $ \hat{\boldsymbol{c}}_{i}=\left(\boldsymbol{\varPhi}^{\mathrm{T}} \boldsymbol{W} \boldsymbol{\varPhi}+\lambda \boldsymbol{J}\right)^{-1} \boldsymbol{\varPhi}^{\mathrm{T}} \boldsymbol{W} \boldsymbol{y}_{i} $ | (4) |
进行FPCA时,为了便于表示,对N个样本函数去均值后仍记为函数{xi(t), i=1, 2, …, N}。样本函数的第一主成分函数(Principal component function, PCF)是指使得样本函数在其上的投影方差最大的L2范数为1的特征函数ξ1(t)。样本函数在ξ1(t)上的投影叫做第一函数型主成分得分(Functional principal component score, FPCS):
| $ f_{i 1}^{\mathrm{FPCA}}=\int_{T} \xi_{1}(t) x_{i}(t) \mathrm{d} t $ | (5) |
求解ξ1(t)的问题可表示为
| $ \begin{aligned} & \max _{\xi_{1}(t)} \frac{1}{N} \sum\limits_{i=1}^{N}\left(f_{i 1}^{\mathrm{FPCA}}\right)^{2}=\max _{\xi_{1}(t)} \frac{1}{N} \sum\limits_{i=1}^{N}\left[\int_{T} \xi_{1}(t) x_{i}(t) \mathrm{d} t\right]^{2} \\ & \text { s. t. }\left\|\xi_{1}(t)\right\|^{2}=\int_{T} \xi_{1}(t) \xi_{1}(t) \mathrm{d} t=1 \end{aligned} $ | (6) |
类似地,求解第m个特征函数ξm(t)就是在满足ξm(t)与前面m-1个特征函数正交的情况下最大化第m阶FPCS的均方。
特征函数ξ(t)满足特征方程[6]:
| $ \int v(s, t) \xi(t) \mathrm{d} t=\rho \xi(s) $ | (7) |
式中:s、t为自变量,
样本函数x=[x1(t), x2(t), …, xN(t)]T的基函数展开式为x=Cϕ,C为N×U阶系数矩阵。特征函数ξ(t)的基函数展开式为ξ(t)=bTϕ,b为系数向量。定义元素为基函数内积的U阶对称矩阵,即Γ=∫ϕϕTdt;用A表示系数向量ci的协方差矩阵,即A=N-1CTC,则式(7)表示为
| $ \boldsymbol{A} \boldsymbol{\varGamma b}=\rho \boldsymbol{b} $ | (8) |
为了防止主成分函数粗糙度过大,求解系数向量b时最大化带有粗糙度惩罚的样本方差:
| $ \max\limits _{\xi(t)} \frac{N^{-1} \sum\limits_{i=1}^{N}\left[\int_{\mathrm{T}} \xi(t) x_{i}(t) \mathrm{d} t\right]^{2}}{\|\xi(t)\|^{2}+\lambda l_{a}(\xi(t))} $ | (9) |
上式的基函数展开形式为
| $ \max \limits_{b} \frac{\boldsymbol{b}^{\mathrm{T}} \boldsymbol{\varGamma} \boldsymbol{A} \boldsymbol{\varGamma} \boldsymbol{b}}{\boldsymbol{b}^{\mathrm{T}} \boldsymbol{\varGamma} \boldsymbol{b}+\lambda \boldsymbol{b}^{\mathrm{T}} \boldsymbol{J} \boldsymbol{b}} $$ $ | (10) |
其广义特征值问题为ΓAΓb=ρ(Γ+λJ)b,进行Cholesky分解Γ+λJ=SST,可转化为对称矩阵特征值分析问题:
| $ \left(\boldsymbol{S}^{-1} \boldsymbol{\varGamma} \boldsymbol{A} \boldsymbol{\varGamma}\left(\boldsymbol{S}^{-1}\right)^{\mathrm{T}}\right)\left(\boldsymbol{S}^{\mathrm{T}} \boldsymbol{b}\right)=\boldsymbol{\rho}\left(\boldsymbol{S}^{\mathrm{T}} \boldsymbol{b}\right) $ | (11) |
求解上式可得到PCF,并保留前M个,记为ξ(t)=[ξ1(t), ξ2(t), …, ξM(t)],ξ(t)为函数型数据内部生成的一组能够表示原始数据的M维正交基函数。采用方差最大化旋转法对ξ(t)进行旋转:
| $ \tilde{\boldsymbol{\xi}}(t)=\boldsymbol{T} \boldsymbol{\xi}(t) $ | (12) |
式中:T为任意M阶正交矩阵,
将样本函数xi(t)分别在ξ(t)和
应用PDA时,首要任务是估计线性微分算子:
| $ L=\beta_{0}(t) I+\cdots+\beta_{K-1}(t) D^{K-1}+D^{K} $ | (13) |
式中:I为恒等算子,β0(t), β1(t), …, βK-1(t)为系数参数,可以是变化的函数,也可以是常系数。
样本函数xi(t)遵循线性微分算子L:
| $ \begin{gathered} L x_{i}(t)=\beta_{0}(t) x_{i}(t)+\cdots+ \\ \beta_{K-1}(t) D^{K-1} x_{i}(t)+D^{K} x_{i}(t) \end{gathered} $ | (14) |
首先考虑不存在强迫函数的情况,即L满足齐次线性微分方程Lxi(t)=0,因此Lxi(t)可视为方程DKxi(t)=-β0(t)xi(t)-…-βK-1(t)DK-1xi(t)提供的拟合残差。若存在与样本函数xi(t)对应的强迫函数αi(t),则线性微分方程Lxi(t)=αi(t)为非齐次,利用最小二乘法定义拟合准则为
| $ \mathop {\min }\limits_L \sum\limits_{i = 1}^N {{{\left\| {L{x_i}(t) - {\alpha _i}(t)} \right\|}^2}} $ | (15) |
基于式(15)的拟合准则,采用逐点最小化方法对线性微分算子L的系数参数进行估计:
| $ \begin{gathered} \min _{L} \sum\limits_{i=1}^{N}\left[L x_{i}(t)-\alpha_{i}(t)\right]^{2}= \\ \min _{L} \sum\limits_{i=1}^{N}\left[\sum\limits_{k=0}^{K} \beta_{k}(t) D^{k} x_{i}(t)-\alpha_{i}(t)\right]^{2} \end{gathered} $ | (16) |
式中βK(t)≡1。其矩阵形式为
| $ \mathop {\min }\limits_L [\boldsymbol{\tau}(t)-\boldsymbol{Z}(t) \boldsymbol{\beta}(t)]^{\mathrm{T}}[\boldsymbol{\tau}(t)-\boldsymbol{Z}(t) \boldsymbol{\beta}(t)] $ | (17) |
式中: τ(t)为元素τi(t)=DKxi(t)构成的N维列向量,β(t)=[β0(t), …, βK-1(t), βK(t)]T为K+1维系数向量,Z(t) 为N×(K+1) 维逐点估计设计矩阵,第i行元素为zi(t)=[-xi(t), …, -DK-1xi(t), αi(t)]。
系数向量解的存在依赖于ZT(t)Z(t)的行列式对于任意t非零。保持t不变,逐点最小化可得
| $ \hat{\boldsymbol{\beta}}(t)=\left[\boldsymbol{Z}^{\mathrm{T}}(t) \boldsymbol{Z}(t)\right]^{-1} \boldsymbol{Z}^{\mathrm{T}}(t) \boldsymbol{\tau}(t) $ | (18) |
对应的线性微分算子L的估计为
| $ \hat{L}=\hat{\beta}_{0}(t) I+\cdots+\hat{\beta}_{K-1}(t) D^{K-1}+D^{K} $ | (19) |
RSQ是常用的度量拟合优度的工具[6]:
| $ d_{\mathrm{RSQ}}=\frac{\sum\limits_{i=1}^{N}\left\|D^{K} x_{i}(t)\right\|^{2}-\sum\limits_{i=1}^{N}\left\|\hat{L} x_{i}(t)\right\|^{2}}{\sum\limits_{i=1}^{N}\left\|D^{K} x_{i}(t)\right\|^{2}} $ | (20) |
式中dRSQ的取值范围为[0, 1],dRSQ越接近1表示线性微分算子L对样本函数的拟合越好。
2.3 主微分得分定理1[18] 设Λ为Hilbert空间,Y是Λ的闭子空间,Y⊥是Y的正交补,任意属于Λ的元素可唯一分解为属于Y的分量和属于Y⊥的分量之和。
根据定理1可知函数{xi(t), i=1, 2, …, N}所属的函数空间可正交分解为两部分,记为ker
将PDA作为数据降维工具时,考虑微分算子的系数为常数的情况,并假设不存在强迫函数。K阶非退化线性微分方程的任意解都可以表示为K个线性无关的复指数函数的线性组合,因此有
| $ \operatorname{ker}(L)=\operatorname{span}\left\{\psi_{1}(t), \psi_{2}(t), \cdots, \psi_{K}(t)\right\} $ | (21) |
式中
| $ \eta^{K}+\hat{\beta}_{K-1} \eta^{K-1}+\cdots+\hat{\beta}_{1} \eta+\hat{\beta}_{0}=0 $ | (22) |
将{ψk(t), k=1, 2, …, K} 作为微分特征函数,类似于FPCS,定义主微分得分为
| $ f_{i K}^{\mathrm{PDA}}=\int_{T} \hat{x}_{i}(t) \psi_{k}(t) \mathrm{d} t $ | (23) |
则fiPDA=[fi1PDA, fi2PDA, …, fiKPDA] 即为PDA提取的样本函数的特征参数。
FPCA和PDA都为样本函数提供了一个降维子空间,区别是FPCA是以函数均值为中心,由函数协方差算子的前M个正交的实特征函数生成,是从几何角度实现降维,而PDA是依靠微分算子对函数前K阶导数线性组合的估计实现的。
3 Relief-F算法特征选择坦克自动装弹机机电系统结构复杂,单一传感器信号无法全面反映系统运行特性。使用FPCA和PDA对多传感器数据进行特征提取时,获取的特征数量可能有几十个甚至上百个,其中可能包含冗余和不相关的特征,并且有限的样本数目下,大量的特征会导致分类识别模型泛化能力差。
Relief-F算法是一种能够处理多分类数据的过滤式特征选择算法,根据特征在不同类别样本之间的差异程度评估特征对分类的相关性。将多传感器数据特征作为第i个样本的
样本fi、fjsame、fjdiff在第
| $ d^{\text {same }}=\sum\limits_{j=1}^{\theta} \frac{\left|f_{i \tilde{m}}-f_{j \tilde{m}}^{\text {same }}\right|}{f_{\tilde{m}}^{\max }-f_{\tilde{m}}^{\min }} $ | (24) |
| $ d^{\mathrm{diff}}=\sum\limits_{\substack{o=1 \\ o \neq \operatorname{class}\left(f_{i}\right)}}^{o} \frac{p(o)}{1-p\left(\operatorname{class}\left(\boldsymbol{f}_{i}\right)\right)} \sum\limits_{j=1}^{\theta} \frac{\left|f_{i \tilde{m}}-f_{j \tilde{m}}^{\text {diff }}\right|}{f_{\tilde{m}}^{\max }-f_{\tilde{m}}^{\min }} $ | (25) |
式中:
设V为抽样次数,则特征权重按照下式更新:
| $ W_{m}=W_{m}-\frac{d^{\text {same }}-d^{\text {diff }}}{V \theta} $ | (26) |
特征的权重越大,表示该特征对类别的敏感性越好。设置权重阈值,筛选多传感器数据特征中权重高于阈值的特征构成新的强相关特征集。
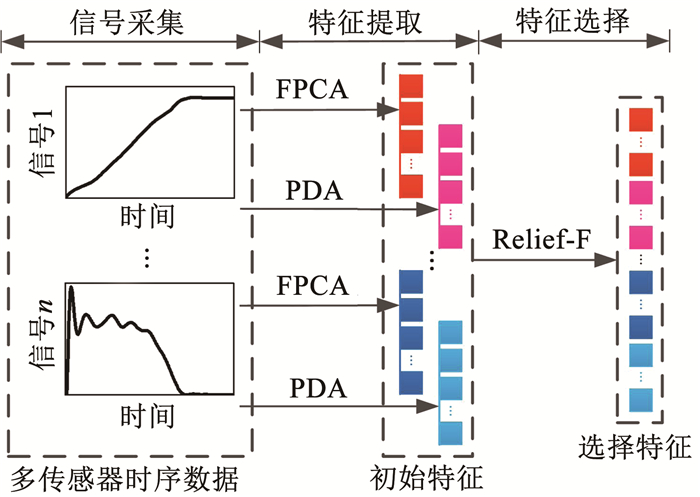
图 1为基于FDA和Relief-F算法的机电系统多传感器时序数据特征提取与选择的过程。使用FPCA和PDA对机电系统运行过程中的多传感器时序数据进行特征提取,所提取的特征构成初始特征集,然后使用Relief-F算法对初始特征进行权重计算与排序,选择与分类问题强相关的特征构成选择特征集,作为ML-KELM的输入信息。
|
图 1 多传感器数据特征提取与选择 Fig. 1 Feature extraction and selection of multi-sensor data |
核极限学习机是基于极限学习机理论与核函数的机器学习算法。极限学习机是一种学习速率快、泛化性能高的单隐含层前馈神经网络,只需设置隐含层节点个数,随机生成隐含层输入权值与偏置,不用进行迭代即可得到最优解[16]。
设训练数据集为{(pi, qi)|i=1, 2, …, N},其中pi为Hin维输入向量,qi为Hout维输出向量。极限学习机第h(h=1, 2, …, Hh)个隐含层节点与输入层、输出层连接权值为ωh=[ωh1, ωh2, …, ωhHin]、γh=[γh1, γh2, …, γhHout],偏置为δh,其学习过程为
| $ \min \limits_{\gamma} \frac{\boldsymbol{\mu}}{2}\|\boldsymbol{H} \boldsymbol{\gamma}-\boldsymbol{Q}\|^{2}+\frac{1}{2}\|\boldsymbol{\gamma}\|^{2} $ | (27) |
式中:μ为正则化系数,γ=[γ1, γ2, …, γHh]T为隐含层输出权值,H=[g(p1), …, g(pN)]T为隐含层输出矩阵,g(·)为激活函数,隐含层对样本pi的映射为g(pi)=[g(ω1·pi+δ1), …, g(ωHh·pi+δHh)],Q=[q1, q2, …, qN]T为目标输出矩阵。
根据Karush-Kuhn-Tucker条件求解上式可得
| $ \hat{\boldsymbol{\gamma}}=\boldsymbol{H}^{\mathrm{T}}\left(\boldsymbol{H} \boldsymbol{H}^{\mathrm{T}}+\frac{\boldsymbol{I}}{\boldsymbol{\mu}}\right)^{-1} \boldsymbol{Q} $ | (28) |
极限学习机隐含层随机性会影响其稳定性。基于Mercer定理,引入核函数F(·)定义核矩阵:
| $ \begin{aligned} \boldsymbol{\varOmega}=\boldsymbol{H} \boldsymbol{H}^{\mathrm{T}}: \varOmega_{i w} & =F\left(\boldsymbol{p}_{i}, \boldsymbol{p}_{w}\right)=g\left(\boldsymbol{p}_{i}\right) g\left(\boldsymbol{p}_{w}\right), \\ i, w & =(1, 2, \cdots, N) \end{aligned} $ | (29) |
则样本pi对应的网络输出可表示为
| $ f\left(\boldsymbol{p}_{i}\right)=g\left(\boldsymbol{p}_{i}\right) \hat{\boldsymbol{\gamma}}=\boldsymbol{\varOmega}_{i} \boldsymbol{\gamma}_{\mathrm{K}} $ | (30) |
式中:Ωi=[F(pi, p1), …, F(pi, pN)] 为样本pi的隐含层输出,γK =(Ω+I/μ)-1Q为隐含层输出权值。由此可避免隐含层随机性对分类结果的影响。
4.2 ML-KELM特征ML-KELM是基于深度学习的思想,利用多个KELM-AE堆叠而成的。KELM-AE是输出信息与输入信息一致的KELM,具有自动编码器特征表示的能力,其结构如图 2所示。

|
图 2 KELM-AE Fig. 2 KELM-AE |
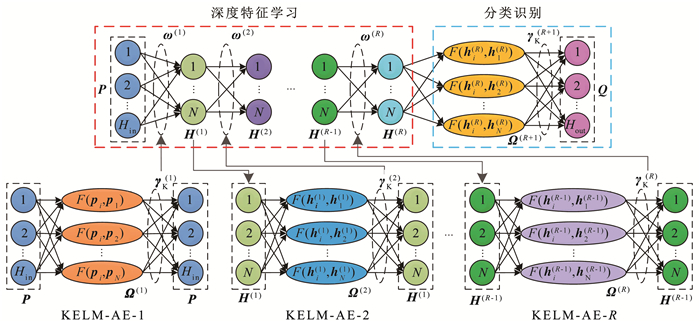
ML-KELM的学习过程分为:1)多层堆叠网络深度特征学习。将ML-KELM前一个隐含层的输出作为后一个KELM-AE的输入,同时KELM-AE的输出权值作为下一个隐含层的输入权值,逐层训练学习到更抽象的融合特征;2)KELM分类识别。将经过多层网络提取的特征作为顶层KELM的输入训练分类器。整个网络的各个权值参数由KELM-AE和KELM单独确定,无需进行微调。ML-KELM的网络结构如图 3所示。
|
图 3 ML-KELM网络结构 Fig. 3 ML-KELM network structure |
设ML-KELM有R+1个隐含层,前R个隐含层的激活函数为g(·),网络需要学习的权值参数为(ω(1), ω(2), …, ω(R), ω(R+1))。ML-KELM第r-1层隐含层输出为H(r-1),将其作为第r个KELM-AE的输入与输出(本文中第1个KELM-AE的输入H(0)为多传感器数据特征),根据KELM的推导:
| $ \boldsymbol{\varOmega}^{(r)} \boldsymbol{\gamma}_{\mathrm{K}}^{(r)}=\boldsymbol{H}^{(r-1)} $ | (31) |
| $ \boldsymbol{\gamma}_{\mathrm{K}}^{(r)}=\left(\boldsymbol{\varOmega}^{(r)}+\frac{\boldsymbol{I}}{\mu_{r}}\right)^{-1} \boldsymbol{H}^{(r-1)} $ | (32) |
将γK(r)作为ML-KELM第r个隐含层的输入权值,则ML-KELM第r个隐含层的输出为
| $ \begin{gathered} \boldsymbol{H}^{(r)}=\left[\boldsymbol{h}_{1}^{(r)}, \boldsymbol{h}_{2}^{(r)}, \cdots, \boldsymbol{h}_{N}^{(r)}\right]= \\ g\left[\boldsymbol{H}^{(r-1)} \boldsymbol{\omega}^{(r)}\right]=g\left[\boldsymbol{H}^{(r-1)}\left(\boldsymbol{\gamma}_{\mathrm{K}}^{(r)}\right)^{\mathrm{T}}\right] \end{gathered} $ | (33) |
得到ML-KELM第R个隐含层的输出H(R)后,利用一个KELM模型得到样本的网络输出:
| $ \boldsymbol{\varOmega}^{(R+1)} \boldsymbol{\gamma}_{\mathrm{K}}^{(R+1)}=\boldsymbol{Q} $ | (34) |
| $ \boldsymbol{\gamma}_{\mathrm{K}}^{(R+1)}=\left(\boldsymbol{\varOmega}^{(R+1)}+\frac{\boldsymbol{I}}{\mu_{R+1}}\right)^{-1} \boldsymbol{Q} $ | (35) |
训练ML-KELM需要确定R个KELM-AE和顶层KELM的核函数参数与正则化系数,使用PSO算法以分类准确率为适应度函数进行寻优选取,自动获取最优的融合特征与分类识别模型。
5 实验分析 5.1 故障识别模型坦克自动装弹机通过机电系统相互衔接的动作完成负载的装填,并且每个动作都规定了相应的性能指标。但由于工作环境恶劣,常常出现机电系统故障导致系统性能指标偏离规定范围的情况,对此本文提出的结合FDA和ML-KELM的机电系统故障识别模型如图 4所示。利用多传感器采集不同故障类别下机电系统运行过程中的时序数据,使用FPCA和PDA将故障引起的时序数据变化特性表征为特征参数,通过Relief-F算法筛选强相关特征作为ML-KELM的输入,相应的类别标签作为输出进行训练,同时使用PSO算法对ML-KELM的参数进行优化选取,获取故障识别模型。将待识别样本数据特征输入最优参数下的ML-KELM进行故障识别,判断故障发生部位。

|
图 4 故障识别模型 Fig. 4 Fault identification model |
为了验证所提方法的可行性,搭建了与某链式输送机原理一致的实验装置,如图 5所示。该装置采用曲线轨道链结构,负载等间距固定在链条上,主动链轮每转动πrad负载移动一个间距。固定负载的链节下端安装带滚轮的组合轴承以支撑负载的主要质量。在上位机中编写控制程序,通过EPOS2控制器驱动Maxon EC45直流电机。主动轴角位移信号由HEDL5540光电编码器测量并通过控制器反馈到上位机;从动轴角速度信号由中星测控CS-ARS-02B三轴角速度传感器测量,其输出信号由无线电压节点采集并通过无线网关传输至上位机;驱动电机控制电流信号则从控制系统中获取。

|
图 5 链式输送机实验装置 Fig. 5 Chain conveyor experimental setup |
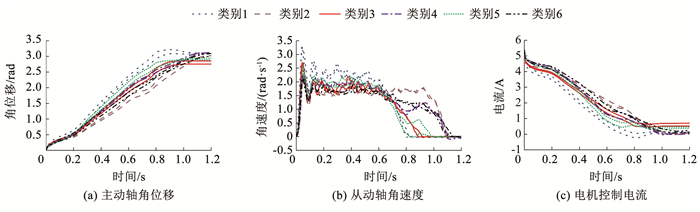
链式输送机的性能指标为在1.2 s的时间内输送负载的定位误差不超过±0.017 5 rad。定位精度超差是其最主要的故障现象之一,进行故障识别实验时,根据经验选取了3种常见的故障因素:①滚轮磨损变形;②链条滚子磨损变形;③电机供电电压不足。将单一因素导致链式输送机发生定位精度超差的情况定义为类别1、类别2和类别3,此外考虑两种因素同时发生,将因素①和②、因素①和③以及因素②和③共同作用的情况定义为类别4、类别5和类别6。通过对1个滚轮进行人为磨损模拟故障因素①,对链条中2个滚子进行人为磨损和塑性变形模拟故障因素②,减小电源电压模拟故障因素③,按照6种类别设置不同程度的故障进行负载输送实验,采集记录运行过程中的主动轴角位移、从动轴角速度以及电机控制电流信号,每种类别进行了50次实验,共获取了300组样本数据。图 6给出了每种类别的2组样本数据,同一类别样本数据具有相似的变化趋势,不同类别样本数据变化趋势则有所差异,并且在系统运行过程的不同阶段,这种差异程度也不同,表明不同故障因素对系统运行过程的影响方式和程度不同,FPCA和PDA就是通过挖掘时序数据的这种变化特性实现特征提取。
|
图 6 样本数据 Fig. 6 Sample data |
使用节点间距为0.05 s的6阶B样条基函数、平滑参数为0.001的2阶粗糙惩罚函数对300组主动轴角位移、从动轴角速度和电机控制电流数据进行函数化,得到的样本函数分别记为X1、X2和X3。进行FPCA时,计算了前10阶PCF及其旋转PCF,图 7为前10阶PCF。将样本函数去均值后与所保留的PCF和旋转PCF进行内积计算得到FPCS作为样本函数的特征参数,分别记为F1FPCA、F2FPCA、F3FPCA、

|
图 7 样本函数的PCF Fig. 7 PCF of sample functions |
在对样本函数进行PDA时,需要确定线性微分算子的阶数。分别对样本函数X1、X2和X3计算了2阶、3阶和4阶线性微分算子,其系数参数与对样本函数的拟合优度见表 1。根据dRSQ值可知,对于样本函数X1,3阶线性微分算子的拟合最好,对于样本函数X2和X3,4阶微分算子的拟合最好。分别求解各微分算子对应的式(22)特征方程的特征根,见表 2,对应的复指数函数如图 8所示,将其作为微分特征函数,进而计算PDS,分别记为F1FDA、F2FDA和F3FDA。
| 表 1 不同阶微分算子的系数参数与拟合优度 Tab. 1 Coefficient parameters and goodness-of-fit of different order differential operators |
| 表 2 特征根 Tab. 2 Characteristic roots |

|
图 8 样本函数的微分特征函数 Fig. 8 Differential eigenfunctions of sample functions |
最终FPCA和PDA提取的主动轴角位移信号、从动轴角速度信号和控制电流信号的特征维数分别为23维、24维和24维,图 9为归一化后的特征参数。将FPCA和PDA提取的多传感器时序数据特征串联得到71维的初始特征集Finitial。使用Relief-F算法计算特征的权重,设置权重阈值为0.8,选择权重值大于0.8的特征形成40维的选择特征集Fselection,如图 10所示。

|
图 9 归一化后的特征参数 Fig. 9 Normalized feature parameters |

|
图 10 特征权重 Fig. 10 Feature weights |
使用ML-KELM进行故障识别时,首先要确定ML-KELM的隐含层数目。设定隐含层数目为1~5层(1层即为一般的KELM)进行测试,分别将初始特征集Finitial和选择特征集Fselection作为ML-KELM的原始输入,输出为样本对应的类别标签。ML-KELM中的核函数使用高斯核函数,PSO算法参数按照经验值设定。从300个样本中随机选取240个作为训练样本,其余作为测试样本,训练样本和测试样本中各类别样本数目是不均衡的,通过10次测试综合评价ML-KELM在不同训练样本下的分类识别能力,结果见表 3。
| 表 3 不同隐含层数目ML-KELM的10次识别准确率 Tab. 3 10 times identification accuracy of ML-KELM with different number hidden layers |
由表 3可知,使用KELM和2层隐含层的ML-KELM时,基于Finitial的故障识别结果较好;当ML-KELM隐含层数目超过2层时,基于Fselection的故障识别结果较好,并且3层隐含层的ML-KELM识别结果最优,10次测试识别准确率的平均值为99.67%,标准差为0.67%,但隐含层数目继续增加时ML-KELM性能开始下降。这是由于KELM-AE对信息进行重构时存在误差,ML-KELM隐含层数目过多会导致特征信息损失增加,造成ML-KELM训练误差增大,分类识别准确率降低。因此选用3层隐含层的ML-KELM。
使用3层隐含层的ML-KELM,分别以FPCA和PDA提取的单一传感器时序数据的单一特征、单一传感器时序数据的多特征以及多传感器时序数据的多特征经过Relief-F算法得到的选择特征作为原始输入,同样地每次从300个样本中随机选取240个作为训练样本,其余作为测试样本,进行了10次分类测试,测试结果见表 4。对于单一传感器时序数据,FPCA和PDA都能够提供一个有限维的特征投影子空间,为ML-KELM提供有效的特征参数,其中对于主动轴角位移信号,基于PDS的识别准确率介于基于FPCS和旋转FPCS的识别准确率之间;对于从动轴角速度信号和电机控制电流信号,基于FPCS和旋转FPCS的识别准确率均高于基于PDS的识别准确率。FPCA和PDA提取的特征具有一定的互补性,基于单一传感器时序数据的多特征能够提高故障识别的准确率。并且不同传感器时序数据特征对不同故障类别的敏感程度具有差异性,使用多传感器时序数据的多特征能够进一步实现特征互补,提高故障识别准确率,其中基于从动轴角速度信号和电机控制电流信号的多特征的故障识别准确率最高,10次测试准确率平均值和标准差分别为99.83%和0.50%。因此对于该链式输送机实验装置,基于FPCA和PDA提取的从动轴角速度信号和电机控制电流信号特征中的强相关特征,使用3层隐含层的ML-KELM能够实现较为准确的故障识别。
| 表 4 基于不同特征的故障识别准确率 Tab. 4 Fault identification accuracy based on different features |
1) 链式输送机运行过程中诸如角位移、角速度等时序信号中包含由故障引起的特征信息,函数型数据分析方法能够将这些具有平滑特性的时序数据表示为连续的函数,挖掘函数的变化特性。
2) FPCA和PDA都能够为样本函数提供一个有效的降维子空间,从不同角度实现样本函数的特征提取,二者的本质决定了FPCA能够获取更丰富的特征参数,但基于函数型主成分得分的分类识别并不总是优于基于主微分得分的分类识别。
3) 多传感器数据特征具有互补性,Relief-F能够从多传感器数据特征中选取强相关的特征,并且使用3层隐含层的ML-KELM进行深度特征学习能够得到最优的融合特征,具有较高的识别准确率。
4) 链式输送机实验装置的故障识别实验初步验证了所提方法的有效性,为坦克自动装弹机中的机电系统故障识别研究提供了一种参考。
| [1] |
赵书涛, 王二旭, 陈秀新, 等. 声振信号联合1D-CNN的大型电机故障诊断方法[J]. 哈尔滨工业大学学报, 2020, 52(9): 116. ZHAO Shutao, WANG Erxu, CHEN Xiuxin, et al. Fault diagnosis method for large motor based on sound-vibration signal combined with 1D-CNN[J]. Journal of Harbin Institute of Technology, 2020, 52(9): 116. DOI:10.11918/201901221 |
| [2] |
QIAN Weiwei, LI Shunming. A novel class imbalance-robust network for bearing fault diagnosis utilizing raw vibration signals[J]. Measurement, 2020, 156: 107567. DOI:10.1016/j.measurement.2020.107567 |
| [3] |
MOGHADAM F K, NEJAD A R. Theoretical and experimental study of wind turbine drivetrain fault diagnosis by using torsional vibrations and modal estimation[J]. Journal of Sound and Vibration, 2021, 509: 116223. DOI:10.1016/j.jsv.2021.116223 |
| [4] |
赵抢抢, 侯保林. 自动弹仓虚拟样机修正的故障定位与诊断[J]. 哈尔滨工程大学学报, 2017, 38(3): 440. ZHAO Qiangqiang, HOU Baolin. Fault location and diagnosis for the modification of the virtual prototype of an automatic shell magazine[J]. Journal of Harbin Engineering University, 2017, 38(3): 440. DOI:10.11990/jheu.201604023 |
| [5] |
LONG Jianyu, MOU Jindong, ZHANG Liangwei, et al. Attitude data-based deep hybrid learning architecture for intelligent fault diagnosis of multi-joint industrial robots[J]. Journal of Manufacturing Systems, 2021, 61: 736. DOI:10.1016/j.jmsy.2020.08.0100 |
| [6] |
RAMSAY J O, SILVERMAN B W. Functional data analysis[M]. 2nd ed. New York: Springer, 2005. DOI:10.1007/b98888
|
| [7] |
高学星, 侯保林, 孙华刚. 基于FDA和神经网络的弹药协调器故障诊断[J]. 南京理工大学学报, 2015, 39(6): 711. GAO Xuexing, HOU Baolin, SUN Huagang. Fault diagnosis of shell transfer arm based on FDA and neural network[J]. Journal of Nanjing University of Science and Technology, 2015, 39(6): 711. DOI:10.14177/j.cnki.32-1397n.2015.39.06.013 |
| [8] |
ZHOU Xin, LEI Xianqing. Fault diagnosis method of the construction machinery hydraulic system based on artificial intelligence dynamic monitoring[J]. Mobile Information Systems, 2021, 2021: 1. DOI:10.1155/2021/1093960 |
| [9] |
WANG Shanshan, JANK W, SHMUELI G, et al. Modeling price dynamics in eBay auctions using differential equations[J]. Journal of the American Statistical Association, 2008, 103(483): 1100. DOI:10.1198/016214508000000670 |
| [10] |
STANISWALIS J G, DODOO C, SHARMA A. Local principal differential analysis: Graphical methods for functional data with covariates[J]. Communications in Statistics-Simulation and Computation, 2017, 46(3): 2346. DOI:10.1080/03610918.2015.1043387 |
| [11] |
JANG E, LIM Y. Classification via principal differential analysis[J]. Communications for Statistical Applications and Methods, 2021, 28(2): 135. DOI:10.29220/csam.2021.28.2.135 |
| [12] |
PAN Yubin, HONG Rongjing, CHEN Jie, et al. Performance degradation assessment of a wind turbine gearbox based on multi-sensor data fusion[J]. Mechanism and Machine Theory, 2019, 137: 509. DOI:10.1016/j.mechmachtheory.2019.03.036 |
| [13] |
TAO Xinmin, REN Chao, LI Qing, et al. Bearing defect diagnosis based on semi-supervised kernel local fisher discriminant analysis using pseudo labels[J]. ISA Transactions, 2021, 110: 394. DOI:10.1016/j.isatra.2020.10.033 |
| [14] |
GUAN Qingfeng, REN Shuliang, CHEN Lirong, et al. A spatial-compositional feature fusion convolutional autoencoder for multivariate geochemical anomaly recognition[J]. Computers & Geosciences, 2021, 156: 104890. DOI:10.1016/j.cageo.2021.104890 |
| [15] |
HE Zhaopeng, SHI Tielin, XUAN Jianping. Milling tool wear prediction using multi-sensor feature fusion based on stacked sparse autoencoders[J]. Measurement, 2022, 190: 110719. DOI:10.1016/j.measurement.2022.110719 |
| [16] |
KASUN L L C, ZHOU Hongming, HUANG Guangbin, et al. Representational learning with ELMs for big data[J]. The Missouri Review, 2013, 28: 31. DOI:10.1109/MIS.2013.140 |
| [17] |
LI Jiaojiao, XI Bobo, DU Qian, et al. Deep kernel extreme-learning machine for the spectral-spatial classification of hyperspectral imagery[J]. Remote Sensing, 2018, 10(12): 2036. DOI:10.3390/rs10122036 |
| [18] |
LAX P D. 泛函分析[M]. 侯成军, 王利广, 译. 北京: 人民邮电出版社, 2010 LAX P D. Functional analysis[M]. HOU Chengjun, WANG Liguang, Translate. Beijing: Posts & Telecom Press, 2010 |
 2023, Vol. 55
2023, Vol. 55


