2. 中国地震局地震工程与工程振动重点实验室(中国地震局工程力学研究所),哈尔滨 150080
2. Key Lab of Earthquake Engineering and Engineering Vibration of China Earthquake Administration (Institute of Engineering Mechanics, China Earthquake Administration), Harbin 150080, China
基于能量的抗震设计方法考虑了地震动持时对结构的影响,自Housner[1]提出基于能量的设计与分析方法以来,输入能量在此基础上被广泛研究[2-5],包括对输入能量、滞回耗能及其对结构响应的影响等。Uang等[6]研究了相对与绝对输入能量的差异,发现两种输入能量在长、短周期内均存在差异,但在中周期范围内结果相似;Gong等[7]建立了两种输入能量谱的衰减关系,发现延性因子对输入能量影响显著;Sucuoǧlu等[8]研究了输入能量对地震动特征的敏感程度,发现峰值速度与峰值加速度的比值(Vpg/Apg)是影响地震能量耗散的重要参数;Decanini等[9]研究了地震动输入能量随震源距衰减关系,发现用最大输入能量EI来评估衰减规律,结果与用峰值加速度(Apg)和峰值速度(Vpg)来评估呈现完全不同的趋势;肖明葵等[10]对多种结构类型在罕遇地震作用下的总输入能量及其影响因素进行分析,提出了多自由度体系及弹塑性体系的简化研究方法。
输入能量数值大小主要受强度指标、阻尼比等因素影响。Ganjavi等[11]发现EI/M、Ia、Vca、Id等强度指标对输入能量的影响存在显著差异,并提出了一种最优的无量纲强度指标(NE)作为归一化能量指标;Benevento等[12]分析了西班牙48次地震,发现VD/VE能够较好地评估地震动输入能量对结构破坏的影响;Fajfar等[13]提出了3个无量纲参数(R、γ、EH/EI)用于简化能量方法分析过程,并认为在实际设计过程中对能量谱进行适当简化不会影响设计准确性;王德才等[14]基于中国场地分类,分析了输入能量与12个强度指标在各周期段的相关性,发现与输入能量相关性最好的强度指标是Ie,并提出了新强度指标Te,该指标能够较好地体现震级、距离等因素对地面运动的影响。
以阻尼比研究为基础的阻尼器在建筑结构耗能减震方面应用广泛[15],Zahrah等[16]等通过研究单自由度体系能量吸收,发现阻尼耗能会影响结构损伤参数的数值;Nurtuǧ等[3]建立了弹性单自由度体系在地震动作用下耗能的简单分析方法,发现阻尼比影响弹性体系耗能,但当体系发生非弹性反应时,结构耗能需求对阻尼比并不敏感。何利等[17]研究了复合强度指标对弹塑性输入能量谱的影响,发现随着阻尼比的增大,弹塑性输入能量谱的峰值有所下降。周颖等[18]发现阻尼比对输入能量谱的影响在不同周期范围内有显著差异,但都有明显的削峰现象。程光煜等[19]发现阻尼比和延性系数对能量谱的峰值有很大影响,在长周期范围内,延性系数一致,随着阻尼比的增大,能量谱的峰值也有所增大。
随着海洋开发战略的发展,近海工程的兴建,这就对海域工程结构抗震设防提出了更高要求。而海域和陆域地震动特征存在差异,主要表现在幅值、频谱等特征。就幅值而言,海域和陆域地震动的Apg无较大差异,而海域地震动的Vpg值较陆域大[20];就反应谱而言,当周期小于0.5 s时,海域和陆域地震动的差异较小,但当周期大于0.5 s时,海域地震动的反应谱较大[21]。此外,同陆域地震动相比,海域地震动含有丰富的长周期成分[22]。随着基于性态的抗震设计的发展[23],研究海域地震动输入能量谱能够为近海域地区的海域结构的基于性态的抗震设防提供参考。概率地震危险性分析(PSHA)是基于性态的抗震设计中重要的一环,为给陆域PSHA提供参考,Cheng等[24-25]先后研究了基于地质统计工具的输入能量空间互相关模型和输入能量与强度指标的经验相关性。目前对输入能量谱的研究主要集中于陆域地震动,针对海域地震动输入能量以及海陆震动的输入能量谱差异的相关研究较少。为给海域PSHA研究提供参考,基于271次地震的6 264条海陆地震动记录,通过相关性分析的方法,从强度指标和阻尼比两个角度进行研究,并对比了海陆的相对与绝对输入能量和强度指标的相关性。
1 海域和陆域地震动数据海域和陆域地震动数据选自日本K-NET台网,包括陆域台站和相模湾海域6个海底台站(ETMC)。共选取了271次地震事件,其中海底台站记录到的地震事件为264次,陆域台站记录到的地震事件为213次,海陆共同记录到的206次,共计3 132组双向水平地震动数据,其中海域地震动数据892组,陆域地震动数据2 240组。海陆台站的位置及地震震中位置见图 1。

|
图 1 海陆台站及地震震中 Fig. 1 Offshore and onshore stations and epicenters of earthquakes |
由于震中距会影响相关性,因此需对地震动记录按照距离分组,在每组数据尽可能平均的前提下将海陆的地震动记录按震中距分为3组:0~60 km、60~100 km、100~300 km,矩震级(Mw)与震中距关系见图 2。在使用K-NET数据研究前,需处理数据,首先进行基线校正使地震动记录回归零基线位置;然后通过滤波去除地震动记录的高频和低频“噪声”。采用Boore等[26-27]提出的基线校正方法,将加速度、速度和位移分别处理。由于峰值位移(Dpg)等位移类强度指标对基线校正较敏感,为保证数据主要信息不丢失以及防止地震动位移时程失真,对加速度记录采用4阶Butterworth非因果滤波器进行滤波,选用带通滤波器,截止频率为0.05~25.00 Hz,并对加速度记录事件前后补零,用足够长的零扩展记录,在所有分析中保留这些零填充部分可避免兼容性问题,且后续不需要进一步校正[28-29]。

|
图 2 海陆震动记录震级与震中距关系 Fig. 2 Relationship between magnitude and epicentral distance of offshore and onshore ground motion records |
由于坐标系选取不同,单自由度体系在水平地震动作用下存在两种形式的运动方程[6],在绝对坐标系下的运动形式见图 3(a),其运动方程为
| $m \ddot{x}_{\mathrm{t}}+c \dot{x}+f_{\mathrm{s}}=0$ | (1) |

|
图 3 水平地震动作用下单自由度体系运动模型 Fig. 3 Model of SDOF system motion under horizontal ground motion |
式中:m为单自由度体系的质量,c为黏滞阻尼系数,fs为体系恢复力,xt为质点绝对位移,其值等于地面运动位移(xg)与质点相对位移(x)之和,
根据其运动方程,可推导出弹性输入能量表达式,在绝对坐标系下弹性输入能量(以下简称绝对输入能量)的计算公式为
| $E_{\mathrm{a}}=\int m \ddot{x}_{\mathrm{t}} \mathrm{d} x_{\mathrm{g}}$ | (2) |
在相对坐标系下,单自由度体系的运动形式见图 3(b),其运动方程为
| $m \ddot{x}_{\mathrm{t}}+c \dot{x}+f_{\mathrm{s}}=-m \ddot{x}_{\mathrm{g}}$ | (3) |
在相对坐标系下的弹性输入能量(以下简称相对输入能量)的计算公式为
| $E_{\mathrm{r}}=-\int m \ddot{x}_{\mathrm{g}} \mathrm{d} x$ | (4) |
为消除结构质量影响,在地震动输入能量研究中,通常用其等效速度代替输入能量[6],其公式为:
| $V_{\mathrm{a}}=\sqrt{\frac{2 E_{\mathrm{a}}}{m}}$ | (5) |
| $V_{\mathrm{r}}=\sqrt{\frac{2 E_{\mathrm{r}}}{m}}$ | (6) |
多种强度指标曾被定义来表征地震动强度,由于地震动和结构的复杂性,一些研究根据不同的研究对象选择强度指标,但没有明确的单一强度指标可以完整地表征地震动破坏势[30]。地震动对结构的破坏能力主要与地震动的持时、幅值以及频谱有关[31]。因此为选取代表性强度指标,筛选了20个常用的强度指标,涵盖了地震动三要素:幅值、持时以及频谱,见表 1,表中T为单自由度体系的自振周期。括号持时是指地震动首末两次达到所规定的阈值所经历的总时间,考虑到海域地震动记录的峰值加速度较小,因此将括号持时的阈值设为5 cm·s-2。
| 表 1 常用的强度指标 Tab. 1 Frequently used intensity measures |
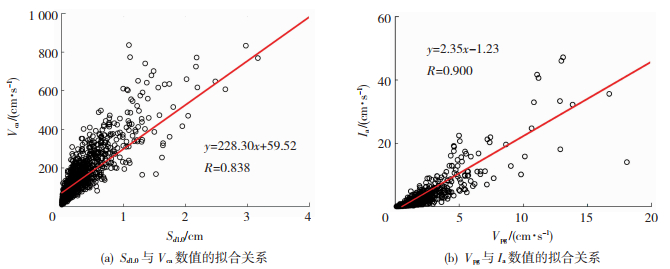
通过计算不同强度指标之间的Pearson相关系数,来确定代表性的强度指标。基于所选地震动记录计算了强度指标间的相关性,结果见表 2,根据强度指标间的相关性,同时综合考虑幅值、持时、频谱,最终选取7个强度指标,分别是:Vpg、Db、Vmi、Vca、Sv0.2、Sd1.0、Ia。以Vca与Sd1.0、Vpg与Ia为例绘制散点图,从图 4的拟合效果可看出两对强度指标有较好相关性,图中R为Pearson相关系数。
| 表 2 初步筛选的20个强度指标间的相关系数(绝对值) Tab. 2 Correlation coefficients of between the 20 preliminarily screened intensity measures (absolute value) |
|
图 4 两对强度指标的线性拟合关系 Fig. 4 Linear fitting relationship of two pairs of intensity measures |
基于上述7个强度指标,为全面解释其与地震动输入能量之间的关系,根据不同震中距和阻尼比分组计算了所选地震动在不同工况下的绝对和相对输入能量(Ea和Er),并分析了其与强度指标的相关性及其海陆差异。由于不同自振周期的结构对强度指标敏感程度不同,且所选7个强度指标并非在所有周期段与输入能量相关性规律都相同,因此需进行周期段划分。翟长海[32]将单自由度体系的自振周期(T)划分为3个周期段:当T ≤ 0.5 s时为短周期;当0.5 s < T≤ 1.5 s时为中周期;当T>1.5 s时为长周期。Uang等[6]认为0.2 s是短周期结构的代表值,当T < 0.2 s时,实际结构尤其是海域结构中并不常见,因此周期段划分如下:当0.2 s ≤T≤ 0.5 s时为短周期;0.5 s < T≤ 1.5 s时为中周期;T>1.5 s时为长周期。
4.1 不同距离下输入能量与强度指标的相关性分析由于近场和远场地震动特征存在很大差异,因此基于震中距分组,分别计算了所选海域与陆域地震动阻尼比为0.05时的Ea和Er,并将其结果与所选强度指标进行相关性分析。在不同震中距下,研究了海域与陆域地震动的不同强度指标与输入能量的相关性。由于Pearson相关系数易受到极端值的影响,基于震中距分组的数据量较少,因此本节选用Spearman相关系数,其计算公式为
| $r=\frac{\sum\limits_{i=1}^n\left(X_i-\bar{X}\right)\left(Y_i-\bar{Y}\right)}{\sqrt{\sum\limits_{i=1}^n\left(X_i-\bar{X}\right)^2 \sum\limits_{i=1}^n\left(Y_i-\bar{Y}\right)^2}}$ | (7) |
X=(X1, X2, …, Xn), Y=(Y1, Y2, …, Yn) 分别为X和Y的两个样本,X、Y分别为样本的平均值,统计学上可证明,样本相关系数r是总体相关系数R的无偏估计量,即有R=r。R的范围为-1~1,R的绝对值越大,相关程度越高。
图 5为不同震中距下的海域与陆域地震动Ea与不同强度指标的相关系数。在不同周期段,与海域和陆域地震动Ea相关性最好的强度指标存在微小差异,具体表现在相关系数的数值上。在短周期范围内,与海域和陆域地震动Ea相关程度最好的强度指标都是Ia,这与叶列平等[31]的研究成果一致,叶列平等[31]发现以Apg为代表的第一类强度指标在短周期范围内,与单自由度体系在地震作用下的响应相关程度较高,Ia为该类强度指标。而在中长周期范围内,与海域和陆域地震动Ea相关性最好的强度指标都是Sd1.0,随着自振周期的增大,Sd1.0与其相关性呈现先上升后下降趋势,在T=1.0 s时达到最大,由此可见在中长周期范围内Ea与Sd1.0有较好相关性,这一结论与谭景阳等[33]的研究结果相似,谭景阳等[33]发现Dpg与海域长周期结构在地震作用下的响应相关性最好,根据叶列平等[31]的定义,Sd1.0与Dpg同为第三类强度指标。

|
图 5 海陆强度指标与Ea的相关系数 Fig. 5 Correlation coefficient between offshore and onshore intensity measures and absolute input energy Ea |
对比图 5(a)、(c)、(e)和图 5(b)、(d)、(f)可发现,海域和陆域地震动Ea与7个强度指标在不同震中距情况下的相关性呈现4种结果:1)Sd1.0与海域和陆域地震动Ea的相关性在3个震中距情况下所呈现的趋势一致,即相关性先上升后下降,当周期约为1.0 s时,达到最大;2)Vca与海域地震动Ea的相关性趋势在各震中距条件下一致,即在短周期范围内上升,在中长周期范围内保持相对稳定,而Vca与陆域地震动Ea在0~60 km、60~100 km震中距情况下的相关系数存在1个极大值和1个极小值,极大值出现在0.3 s附近,极小值出现在1.0 s附近,而其在100~300 km震中距情况下只有1个极小值;3)Db与海域地震动Ea的相关性在0~60 km情况下先升高后趋于稳定,在60~100 km、100~300 km的情况下,Db与海域地震动Ea的相关系数存在两个极值,1个极大值1个极小值,而陆域地震动Ea与Db的相关性在各震中距范围下,均存在两个极值,即1个极大值和1个极小值;4)Vpg、Vmi、Sv0.2、Ia与海域和陆域地震动相关程度均随着震中距的增加而降低且都只有1个极小值,所不同的是,海域地震动Ea与上述4个强度指标相关系数的极值出现在1.0 s后,海域地震动Ea与其相关系数的极值出现在1.0 s前。
图 6为不同震中距下的海域和陆域地震动Er与不同强度指标的相关系数。Sv0.2在T=0.2 s时相关程度高于其他强度指标,但其相关系数值迅速下降。在短周期范围内,与海域和陆域Er相关性最好且较为稳定的强度指标仍是Ia;在中周期范围内,与海域和陆域Er相关性最好的是Sd1.0,相关解释已在4.1.1节中描述;在长周期范围内,Sd1.0与海域和陆域Er的相关性呈现下降趋势,但Vpg、Vmi与海域和陆域Er的相关性呈现上升趋势,最终相关系数值大于Sd1.0。不同周期段差异与Uang等[6]在关于Ea与Er在不同周期段的差异的研究结果一致。

|
图 6 海陆强度指标与Er的相关系数 Fig. 6 Correlation coefficient between offshore and onshore intensity measures and relative input energy Er |
对比图 6(a)、(c)、(e)和图 6(b)、(d)、(f)可发现,海域和陆域地震动Er与7个强度指标在不同震中距相关性结论与Ea基本一致。因此,震中距会影响地震动Er与强度指标的相关程度,具体体现在影响相关系数大小、极值个数以及造成海陆差异。海域和陆域的Ea、Er在不同震中距以及不同周期段与其他强度指标的相关性情况见表 3。
| 表 3 不同工况下与地震动输入能量相关性最好的强度指标 Tab. 3 Intensity measures that have the best correlation with the input energy of ground motions under different conditions |
在研究阻尼比对海域和陆域地震动Ea和Er与强度指标相关性的影响时,分别分析了第3节所筛选的7个强度指标在不同阻尼比下与Ea和Er的相关性。海陆震动Ea与在不同阻尼比下与所选7个强度指标的相关性见图 7~9,由于结论类似,以图 7所示海域和陆域地震动记录的Ea在不同阻尼比下与Ia的相关性为例对这一结论加以说明。图 7(a)、(b)分别为海陆地震动记录的Ea与Ia的相关系数,对比两图结果可知,海陆地震动Ea与Ia在全周期的相关性程度均随着阻尼比的增大而增大,且随着自振周期T的增大而趋于稳定。

|
图 7 海陆地震动Ea在不同阻尼比下与Ia的相关系数 Fig. 7 Correlation coefficient between Ea of offshore and onshore ground motions and Ia under different damping ratios |

|
图 8 海域地震动Ea在不同阻尼比下与其他强度指标的相关系数 Fig. 8 Correlation coefficient between Ea of offshore ground motion and other intensity measures under different damping ratios |

|
图 9 陆域地震动Ea在不同阻尼比下与其他强度指标的相关系数 Fig. 9 Correlation coefficient between Ea of onshore ground motion and other intensity measures under different damping ratios |
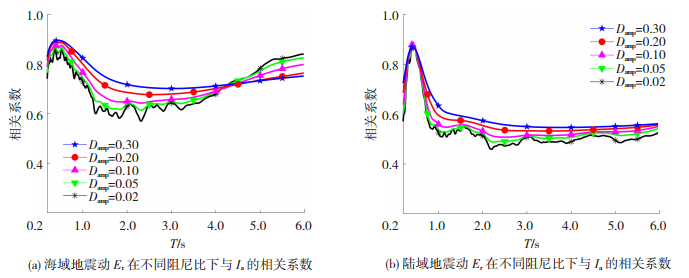
在研究海域和陆域地震动Er在不同阻尼比下与所选强度指标的相关性时,有两种情况:1) 有3个强度指标的分析结果与Ea对应结论相同,即Vca、Db、Sd1.0,海域和陆域地震动Er与Vca、Db、Sd1.0在全周期段相关性均随着阻尼比的增大而增大且其值随着自振周期T的增大而趋于稳定,见图 10~12;2) Ia、Vmi、Vpg、Sv0.2的结果却与上述情况不同,就陆域地震动Er而言,上述4个强度指标与Er在全周期的相关程度随着阻尼比的增大而增大,见图 13(b)、图 15;但海域地震动情况与陆域地震动不同,具体表现为:当自振周期T < 4.0 s时,上述4个强度指标与海域地震动Er的相关程度随着阻尼比的增大而增大,当自振周期T>4.0 s时, 上述4个强度指标与海域地震动Er的相关程度随着阻尼比的增大而减小,见图 13(a)、图 14。

|
图 10 海陆地震动Er在不同阻尼比下与Vca的相关系数 Fig. 10 Correlation coefficient between Er of offshore and onshore ground motions and Vca under different damping ratios |

|
图 11 海域地震动Er在不同阻尼比下与其他强度指标的相关系数 Fig. 11 Correlation coefficient between Er of offshore ground motion and other intensity measures under different damping ratios |

|
图 12 陆域地震动Er在不同阻尼比下与其他强度指标的相关系数 Fig. 12 Correlation coefficient between Er of onshore ground motion and other intensity measures under different damping ratios |
|
图 13 海陆地震动Er在不同阻尼比下与Ia的相关系数 Fig. 13 Correlation coefficient between Er of offshore and onshore ground motions and Ia under different damping ratios |

|
图 14 海域地震动Er在不同阻尼比下与其他强度指标的相关系数 Fig. 14 Correlation coefficient between Er of offshore ground motion and other intensity measures under different damping ratios |

|
图 15 陆域地震动Er在不同阻尼比下与其他强度指标的相关系数 Fig. 15 Correlation coefficient between Er of onshore ground motion and other intensity measures under different damping ratios |
海陆地震动的频率成分存在差异,可能是导致上述现象的原因。通过滤波去掉海域地震动记录的低频成分,将截止频率设置为1.0~25.0 Hz,再将海域地震动记录的Er与Ia、Vmi、Vpg、Sv0.2进行相关性分析,得到与陆域地震动相似的结果,即随着阻尼比的增加,上述4个强度指标与海域地震动记录Er的相关程度随着阻尼比增大而增大,结果见图 16。说明:海域地震动记录低频成分的丰富可能影响了上述强度指标与Er的相关性规律。

|
图 16 海域地震动Er在不同阻尼比下与强度指标的相关系数 Fig. 16 Correlation coefficient between Er of offshore ground motion and intensity measures under different damping ratios |
考虑震中距和阻尼比,研究了海域与陆域地震动输入能量与其他强度指标的相关性,结果表明,海域和陆域地震动输入能量与强度指标的相关性存在异同,主要结论如下:
1) 就不同周期段而言,与海域和陆域Ea相关性最好的强度指标基本一致,即在短周期范围内,与海域和陆域Ea相关性最好的强度指标是Ia,在中长周期范围内,与海域和陆域Ea相关性最好的强度指标Sd1.0;而海域和陆域的Er与所选强度指标的相关性与Ea在中长周期内存在差异,具体表现在Sv0.2、Vpg、Vmi上,在0.2 s时,Sv0.2与海域和陆域的Er相关性最好,Vpg、Vmi与海域和陆域的Er的相关程度在长周期范围内呈现上升趋势,相关系数最终大于Sd1.0。
2) 从不同震中距范围来看,Ea与Er和所选强度指标的相关性趋势一致,但海域和陆域的输入能量与强度指标的相关性趋势存在差异,具体体现在海域和陆域与输入能量相关系数的数值大小、极值个数以及极值出现的周期点。
3) 就不同阻尼比而言,所选强度指标与海域和陆域Ea的相关性趋势一致,即相关性程度均随阻尼比的增大而增大。但与Er相关性趋势存在较大差异,Ia、Vmi、Vpg、Sv0.2与陆域地震动Er相关程度在全周期的相关性程度均随阻尼比的增大而增大,但与海域地震动相关性出现不同情况:当T < 4.0 s时与海域地震动记录的Er相关程度随着阻尼比的增大而增大,但当T>4.0 s时与海域地震动Er相关程度随着阻尼比的增大而减小。初步分析表明:造成此现象的原因可能是海域地震动低频成分较陆域地震动丰富。
| [1] |
HOUSNER G W. Limit design of structures to resist earthquakes[C]//Proceedings of the 1st World Conference on Earthquake Engineering. Berkeley: [s. n.], 1956: 5.1
|
| [2] |
TAKEWAKI I. Frequency-domain analysis of earthquake input energy to structure-pile systems[J]. Engineering Structures, 2005, 27(4): 549. DOI:10.1016/j.engstruct.2004.11.014 |
| [3] |
NURTUǦ A, SUCUOǦLU H. Prediction of seismic energy dissipation in SDOF systems[J]. Earthquake Engineering and Structural Dynamics, 1995, 24(9): 1215. DOI:10.1002/eqe.4290240904 |
| [4] |
MINA M, HAMED S. The effects of ground motion duration and pinching-degrading behavior on seismic response of SDOF systems[J]. Soil Dynamics and Earthquake Engineering, 2018, 114: 333. DOI:10.1016/j.soildyn.2018.06.032 |
| [5] |
TAKEWAKI I, TSUJIMOTO H. Scaling of design earthquake ground motions for tall buildings based on drift and input energy demands[J]. Earthquakes and Structures, 2011, 2(2): 171. DOI:10.12989/eas.2011.2.2.171 |
| [6] |
UANG C M, BERTERO V V. Evaluation of seismic energy in structures[J]. Earthquake Engineering and Structural Dynamics, 1990, 19(1): 77. DOI:10.1002/eqe.4290190108 |
| [7] |
GONG Maosheng, XIE Lili. Study on comparison between absolute and relative input energy spectra and effects of ductility factor[J]. Acta Seismologica Sinica, 2005, 18(6): 726. DOI:10.1007/s11589-005-0099-4 |
| [8] |
SUCUOǦLU H, NURTUǦ A. Earthquake ground motion characteristics and seismic energy dissipation[J]. Earthquake Engineering and Structural Dynamics, 1995, 24(9): 1213. DOI:10.1002/eqe.4290240903 |
| [9] |
DECANINI L D, MOLLAIOLI F. Formulation of elastic earthquake input energy spectra[J]. Earthquake Engineering and Structural Dynamics, 1998, 27(12): 1521. DOI:10.1002/(SICI)1096-9845(199812)27:12<1503:AID-EQE797>3.0.CO;2-A |
| [10] |
肖明葵, 刘波, 白绍良. 抗震结构总输入能量及其影响因素分析[J]. 重庆建筑大学学报, 1996, 18(2): 32. XIAO Mingkui, LIU Bo, BAI Shaoliang. Analysis of the total energy and its influencing factors for seismic structures[J]. Journal of Chongqing Jianzhu University, 1996, 18(2): 32. |
| [11] |
GANJAVI B, REZAGHOLILOU A. An intensity measure for seismic input energy demand of multi- degree-of-freedom systems[J]. Civil Engineering Infrastructures Journal, 2018, 51(2): 385. DOI:10.7508/ceij.2018.02.008 |
| [12] |
BENEVENTO-CLIMENT A, PUJADES L G, LÓPEZ-ALMANSA F. Design energy input spectra for moderate-seismicity regions[J]. Earthquake Engineering and Structural Dynamics, 2002, 31(5): 1171. DOI:10.1002/eqe.153 |
| [13] |
FAJFAR P, VIDIC T. Consistent inelastic design spectra: hysteretic and input energy[J]. Earthquake Engineering and Structural Dynamics, 1994, 23(5): 536. DOI:10.1002/eqe.4290230505 |
| [14] |
王德才, 叶献国, 常磊. 考虑场地条件与设计地震分组的输入能量谱研究[J]. 地震学报, 2011, 33(1): 101. WANG Decai, YE Xianguo, CHANG Lei. A study on input energy spectrum in consideration of site effect and design earthquake classification[J]. Acta Seismologica Sinica, 2011, 33(1): 101. DOI:10.3969/j.issn.0253-3782.2011.01.008 |
| [15] |
骈超, 钱江. 考虑阻尼器极限状态的单自由度体系地震响应[J]. 哈尔滨工业大学学报, 2020, 52(8): 46. PIAN Chao, QIAN Jiang. Seismic response of SDOF systems considering the limit states of viscous dampers[J]. Journal of Harbin Institute of Technology, 2020, 52(8): 46. DOI:10.11918/201910140 |
| [16] |
ZAHRAH T F, HALL W J. Earthquake energy absorption in SDOF structures[J]. Journal of Structural Engineering, 1984, 110(8): 1771. DOI:10.1061/(ASCE)0733-9445(1984)110:8(1757) |
| [17] |
何利, 叶献国. 基于复合强度指标的弹塑性输入能量谱研究[J]. 工程力学, 2013, 30(4): 13. HE Li, YE Xianguo. Research on the elastic-plastic input energy spectra based on compound intensity indicator[J]. Engineering Mechanics, 2013, 30(4): 13. DOI:10.6052/j.issn.1000-4750.2011.11.0791 |
| [18] |
周颖, 宋戈. 单自由度自复位体系设计能量谱研究[J]. 地震工程与工程振动, 2020, 40(2): 11. ZHOU Ying, SONG Ge. Design energy spectra for self-centering SDOF systems[J]. Earthquake Engineering and Engineering Dynamics, 2020, 40(2): 11. DOI:10.13197/j.eeev.2020.02.1.zhouy.001 |
| [19] |
程光煜, 叶列平. 弹塑性SDOF系统的地震输入能量谱[J]. 工程力学, 2008, 25(2): 8. CHENG Guangyu, YE Lieping. Earthquake input energy spectrum for inelastic SDOF systems[J]. Engineering Mechanics, 2008, 25(2): 8. DOI:10.3969/j.issn.1002-8412.2006.05.001 |
| [20] |
DHAKAL Y P, KUNUGI T, SUZUKI W, et al. Strong motions on land and ocean bottom: comparison of horizontal PGA, PGV, and 5% damped acceleration response spectra in Northeast Japan and the Japan Trench Area[J]. Bulletin of the Seismological Society of America, 2021, 111(6): 3237. DOI:10.1785/0120200368 |
| [21] |
谭景阳, 胡进军, 周旭彤, 等. 海底与陆地地震动反应谱比定量分析[J]. 振动与冲击, 2021, 40(2): 219. TAN Jingyang, HU Jinjun, ZHOU Xutong, et al. Quantitative analysis on the difference of spectral ratios between offshore and onshore ground motions[J]. Journal of Vibration and Shock, 2021, 40(2): 219. DOI:10.13465/j.cnki.jvs.2021.02.029 |
| [22] |
陈苏, 周越, 李小军, 等. 近海域地震动的时频特征与工程特性[J]. 振动与冲击, 2018, 37(16): 232. CHEN Su, ZHOU Yue, LI Xiaojun, et al. Time-frequency and engineering characteristics on offshore ground motion[J]. Journal of Vibration and Shock, 2018, 37(16): 232. DOI:10.13465/j.cnki.jvs.2018.16.033 |
| [23] |
谢礼立, 马玉宏, 翟长海. 基于性态的抗震设防与设计地震动[M]. 北京: 科学出版社, 2009: 13. XIE Lili, MA Yuhong, ZHAI Changhai. Performance-based seismic design and design ground motion[M]. Beijing: Science Press, 2009: 13. |
| [24] |
CHENG Yin, LUCCHINI A, MOLLAIOLI F. Ground-motion prediction equations for constant-strength and constant-ductility input energy spectra[J]. Bulletin of Earthquake Engineering, 2020, 18(1): 37. DOI:10.1007/s10518-019-00725-x |
| [25] |
CHENG Yin, LIU Tongtong, WANG Jianfeng, et al. Empirical correlations of spectral input energy with peak amplitude, cumulative, and duration intensity measures[J]. Bulletin of the Seismological Society of America, 2022, 112(2): 978. DOI:10.1785/0120210164 |
| [26] |
BOORE D M, STEPHENS C D, JOYNER W B. Comments on baseline correction of digital strong-motion data: examples from the 1999 Hector Mine, California[J]. Bulletin of the Seismological Society of America, 2002, 92(4): 1546. DOI:10.1785/0120000926 |
| [27] |
BOORE D M, BOMMER J J. Processing of strong-motion accelerograms: needs, options and consequences[J]. Soil Dynamics and Earthquake Engineering, 2005, 25(2): 93. DOI:10.1016/j.soildyn.2004.10.007 |
| [28] |
BOORE D M, AKKAR S. Effect of causal and acausal filters on elastic and inelastic response spectra[J]. Earthquake Engineering and Structural Dynamics, 2003, 32(11): 1729. DOI:10.1002/eqe.299 |
| [29] |
BOORE D M. On pads and filters: processing strong-motion data[J]. Bulletin of the Seismological Society of America, 2005, 95(2): 745. DOI:10.1785/0120040160 |
| [30] |
叶献国. 地震强度指标定义的客观评价[J]. 合肥工业大学学报(自然科学版), 1998(6): 8. YE Xianguo. Objective evaluation on definition of earthquake intensity meassure[J]. Journal of Hefei University of Technology (Natural Science), 1998(6): 8. |
| [31] |
叶列平, 马千里, 缪志伟. 结构抗震分析用地震动强度指标的研究[J]. 地震工程与工程振动, 2009, 29(4): 17. YE Lieping, MA Qianli, MIAO Zhiwei. Study on earthquake intensities for seismic analysis of structures[J]. Earthquake Engineering and Engineering Dynamics, 2009, 29(4): 17. DOI:10.13197/j.eeev.2009.04.019 |
| [32] |
翟长海. 最不利设计地震动研究[D]. 哈尔滨: 中国地震局工程力学研究所, 2002: 39 ZHAI Changhai. Study on the severest real ground motion for seismic design and analysis[D]. Harbin: Institute of Engineering Mechanics, China Earthquake Administration, 2002: 39 |
| [33] |
谭景阳, 胡进军, 谢礼立. 海域地震动长周期特性及其强度指标研究[J]. 振动与冲击, 2021(3): 9. TAN Jingyang, HU Jinjun, XIE Lili. Long-period characteristics of offshore ground motion and its and intensity index[J]. Journal of Vibration and Shock, 2021(3): 9. DOI:10.13465/j.cnki.jvs.2021.03.001 |
 2023, Vol. 55
2023, Vol. 55


