2. 南京工业大学 土木工程学院,南京 211816;
3. 江苏科技大学 土木工程与建筑学院,江苏 镇江 212003;
4. 河南工业大学 土木工程学院,郑州 450001
2. College of Civil Engineering, Nanjing Tech University, Nanjing 211816, China;
3. School of Civil Engineering and Architecture, Jiangsu University of Science and Technology, Zhenjiang 212003, Jiangsu, China;
4. College of Civil Engineering, Henan University of Technology, Zhengzhou 450001, China
纤维增强复合材料(fiber reinforced polymer,简称FRP)型材凭借其轻质高强、抗疲劳、耐腐蚀、可设计、易加工和施工便捷等特点逐渐应用于建筑结构、桥梁结构及特种结构[1-4]。FRP型材是由FRP薄板构成的截面形状为开口(槽形、工字形、L形等)或闭口(矩形、圆形等)截面的薄壁构件。从宏观力学角度看,FRP型材是均质、线弹性及正交各向异性的材料[5]。由于其薄壁截面的几何特性以及相对较低的刚度与强度之比,FRP构件的破坏通常是由其稳定性而非材料强度控制。因此,准确预测屈曲临界力是结构设计中保证FRP构件安全可靠的基础,其中FRP轴心受压构件的屈曲临界力预测是结构设计的第一步。当构件长细比较大时(“长柱”),其破坏模式通常为整体屈曲,其中双轴对称截面构件及绕非对称轴失稳的单轴对称截面构件的破坏模式为弯曲屈曲,而绕对称轴失稳的单轴对称截面构件的破坏模式为弯扭屈曲;当构件长细比较小时(“短柱”),其破坏模式通常为局部屈曲;当构件长细比达到某个范围,使得受压构件的整体屈曲临界力与局部屈曲临界力接近或相等时,其破坏由整体屈曲与局部屈曲相互作用所导致,即耦合屈曲[6]。本文研究对象为弯曲屈曲控制的FRP“长柱”。
近20年来,部分学者通过试验研究、数值计算及理论分析较为全面地研究了FRP轴心受压构件的整体稳定性能。以Barbero[7]、Hashem等[8]为代表的学者认为经典欧拉公式[9]可以较为准确地预测FRP轴压构件的弯曲屈曲临界力。以Zureick[10]、Mottram等[11]和Bank[12]为代表的学者则认为采用Engesser[13]提出的考虑剪切变形影响的修正公式更加合适。同时Kardomateas等[14]推荐采用Haringx[15]提出的考虑剪切变形的修正公式。但Barbero等[16]认为剪切变形对于计算结果的影响很小,可以忽略。另外,Strongwell公司[17]和Fiberline公司[18]根据各自的试验数据给出了预测FRP轴压构件的弯曲屈曲临界力的相关经验公式。总的来说,目前还没有一种被广大学者普遍认同的关于FRP轴压构件整体弯曲屈曲临界力的计算方法。同时,也没有学者通过试验数据客观评估上述5种计算方法的预测精度。
本文收集、挑选了1969—2020年相关文献,建立了包含176根FRP轴压构件弯曲屈曲失效试验数据的数据库。数据库中试验数据的录入经过了严格的挑选(相关筛选条件在下文中介绍),以保证数据库的客观性及可靠性。此数据库在相关计算方法的推导与验证,既有计算方法预测精度的评估以及未来相关数据库的建立等方面都极具参考价值。基于该数据库,分析了目前预测FRP轴压构件弯曲屈曲临界力的5种方法的预测精度。这5种方法为:提出时面向各向同性材料,但后来被广泛应用于FRP杆件预测的经典欧拉公式[9]、Engesser[13]修正公式和Haringx[15]修正公式,以及Strongwell公司[17]与Fiberline公司[18]基于各自FRP杆件试验数据建立的、面向各类FRP杆件的计算公式。同时,基于Perry公式及相关学者的FRP构件初始弯曲的实测值,给出了考虑初始弯曲影响的FRP轴压构件整体稳定系数表达式,使得GB 50017—2017《钢结构设计标准》[19]和欧洲EU3《钢结构设计规范》[20]中用于计算钢构件整体屈曲临界力的计算式可用于计算考虑FRP构件初始弯曲影响的弯曲屈曲临界力。另外,基于数据库,给出了预测FRP轴压构件弯曲屈曲临界力的经验公式。通过试验数据及数值计算,验证并评价了上述两种计算方法的预测精度。
1 既有FRP轴压构件弯曲屈曲临界力计算方法目前,FRP轴心受压构件弯曲屈曲临界力的计算方法主要有Euler[9]、Engesser[13]、Haringx[15]、Strongwell公司[17]与Fiberline公司[18]给出的5类计算式。
1.1 经典欧拉公式对于弯曲屈曲失效的轴心受压FRP构件,Barbero等[7, 16, 21-22]、Hashem等[8]和Seangatith等[23]通过数值计算、试验研究及理论分析认为采用经典欧拉公式[9](式(1))计算得到的FRP构件弯曲屈曲临界力的精度是足够的。
| $ P_{\mathrm{E}}={\rm{ \mathit{π} }}^2 E_{\mathrm{LC}} I_{\min } /\left(K L_{\text {eff }}\right)^2={\rm{ \mathit{π} }}^2 E_{\mathrm{LC}} A_{\mathrm{g}} / \lambda^2 $ | (1) |
其中
| $ \lambda=\frac{K L_{\mathrm{eff}}}{r} $ | (2) |
式中:PE为欧拉临界力,ELC为FRP构件纵向压缩模量,Imin为沿构件弱轴的截面惯性矩,Ag为构件截面面积,K为构件端部约束系数,Leff为构件计算长度,λ为构件长细比,r为沿弱轴的截面回转半径。目前,欧洲复合材料结构设计规范与手册[24]、Bedford公司[25]和Creative公司[26]均采用经典欧拉公式预测FRP轴压构件弯曲屈曲临界力。
1.2 Engesser修正公式FRP型材的特点决定了FRP构件的纵向压缩弹性模量与面内剪切模量的比值(ELC/GLT)相对较高,Richards等[27]通过试验研究建议FRP轴心受压构件弯曲屈曲临界力采用Engesser[13]给出的考虑剪切变形影响的式(3)进行计算。
| $ \begin{aligned} & P_{\mathrm{Esh} 1}=P_{\mathrm{E}} /\left[1+\beta P_{\mathrm{E}} /\left(G_{\mathrm{LT}} A_{\mathrm{g}}\right)\right] \\ & \beta=\frac{A_{\mathrm{g}}}{I^2} \int_0^{A \mathrm{g}} \frac{S^2}{B^2} \mathrm{~d} A_{\mathrm{g}} \end{aligned} $ | (3) |
式中:PEsh1为Engesser临界力,GLT为FRP构件的面内剪切模量,β为与截面形状有关的剪切系数[13-14],I为构件的截面惯性矩,S为截面模量,B为截面宽度。Zureick等[10, 28]、Mottram等[11]、Bank[12]、Roberts[29]、Vanevenhoven等[30]和Boscato等[31]均建议采用Engesser给出的考虑剪切变形影响的式(3)预测FRP构件弯曲屈曲临界力。但Barbero等[16]认为剪切变形对于绕弱轴弯曲屈曲的FRP构件的临界力影响很小,可以忽略不计。
1.3 Haringx修正公式Kardomateas等[14]认为经典欧拉公式高估了FRP构件弯曲屈曲临界力,采用Haringx[15]给出的考虑剪切变形影响的修正公式(式(4))预测其临界力更为合适。
| $ P_{\mathrm{Esh} 2}=\left[\sqrt{1+4 \beta P_{\mathrm{E}} /\left(G_{\mathrm{LT}} A_{\mathrm{g}}\right)}-1\right]\left(G_{\mathrm{LT}} A_{\mathrm{g}} / 2 \beta\right) $ | (4) |
式中PEsh2为Haringx临界力。
1.4 Strongwell公司建议公式Strongwell公司[17]根据其内部试验数据给出了计算不同截面形状的FRP轴压构件弯曲屈曲临界力的经验公式。
工字形截面FRP构件:
| $ P_{\mathrm{ES}}=4.9 E_{\mathrm{LC}} A_{\mathrm{g}} /\left(K L_{\mathrm{eff}} / r\right)^{1.7} $ | (5a) |
L形截面FRP构件:
| $ P_{\mathrm{ES}}=E_{\mathrm{LC}} A_{\mathrm{g}} / 56\left(K L_{\mathrm{eff}} / r\right)^{0.55} $ | (5b) |
FRP方管或圆管:
| $ P_{\mathrm{ES}}=1.3 E_{\mathrm{LC}} A_{\mathrm{g}} /\left(K L_{\mathrm{eff}} / r\right)^{1.3} $ | (5c) |
式中PES为Strongwell临界力。
1.5 Fiberline公司建议公式Fiberline公司[18]同样根据其内部试验数据给出了轴心受压FRP构件弯曲屈曲临界力经验公式:
| $ P_{\mathrm{EF}}=N_{\mathrm{C}} /\left(1+N_{\mathrm{C}} / P_{\mathrm{E}}\right) $ | (6) |
其中
| $ N_{\mathrm{C}}=F_{\mathrm{LC}} A_{\mathrm{g}} $ | (7) |
式中:PEF为Fiberline临界力,NC为FRP短柱材料破坏时的极限荷载,FLC为FRP型材纵向抗压强度。
2 数据库由于FRP构件稳定性能问题的复杂性,可采用试验数据库来评估FRP构件屈曲临界力计算方法。部分学者建立的FRP构件稳定性能的数据库见表 1,Lane等[6]、Barbero等[16]、Vanevenhoven等[30]、Puente等[32]和Lee等[33]广泛收集了当时可查阅文献中关于FRP构件稳定性的试验数据。尽管上述学者建立的数据库包含了FRP构件整体屈曲及局部屈曲的试验数据,但仍有一大部分FRP构件稳定性能的试验数据未包含在上述数据库中。
| 表 1 关于FRP轴压构件屈曲的既有及本文的数据库统计 Tab. 1 Summary of existing and proposed databases for buckling of axially loaded FRP members |
本文通过对1969—2020年相关文献的收集与挑选,建立了迄今为止最全的FRP轴压构件弯曲屈曲失效试验数据的数据库(表 2)。数据库中包含了176根FRP轴压构件弯曲屈曲失效的试验数据,其中包含62根宽翼缘工字形截面FRP构件、9根普通工字形截面FRP构件、61根FRP方管、30根FRP圆管以及14根L形截面FRP构件。FRP构件截面形状见图 1。数据库中的所有FRP试验构件满足以下要求:
| 表 2 FRP轴压构件弯曲屈曲数据库 Tab. 2 Test database for flexural buckling of axially loaded FRP members |

|
图 1 FRP构件截面形状 Fig. 1 Cross-sections of FRP members |
1) 试验构件采用单一种类的纤维及树脂通过拉挤工艺制作;
2) 通过材性试验给出基本的材料性能指标,包含纵向压缩弹性模量(ELC)、纵向压缩极限强度(FLC)及面内剪切模量(GLT);
3) 明确给出试验构件端部约束情况及构件长度或给出构件计算长度(Leff);
4) 明确给出试验构件弯曲屈曲临界力试验结果(Pexp)。
3 既有计算方法比较分析以数据库中试验数据为依据,既有5种计算方法的对比分析见图 2。由于计算式的构成问题,Strongwell公司[17]建议的公式并未在图 2中表示。经典欧拉公式(式(1))高估了FRP构件弯曲屈曲临界力,且预测误差明显大于图 2中其余计算方法。Engesser[13]和Haringx[15]修正公式(式(3)和(4))几乎重合,且两者也均高估了FRP构件弯曲屈曲临界力,但预测误差稍低于经典欧拉公式。这是由于与各向同性材料相比,FRP型材的纵向压缩弹性模量与面内剪切模量的比值(ELC/GLT)相对较高,横向剪切变形对于FRP构件的屈曲临界力影响较为明显,而欧拉公式是面向各向同性材料的。因此,欧拉公式高估了FRP构件弯曲屈曲临界力。由于考虑了剪切变形的影响,Engesser[13]和Haringx[15]修正公式的预测误差与欧拉公式相比稍有降低。Fiberline公司[18]建议公式(式(6))是图中所有计算式中对于FRP构件弯曲屈曲临界力预测最为保守的。

|
图 2 不同计算方法的比较 Fig. 2 Comparison between different calculation methods |
表 3给出了既有计算方法对于数据库中176根FRP轴压构件弯曲屈曲临界力预测情况的统计,并采用平均绝对误差A1(式(8))、预测值与试验值比值的平均值A2(式(9))及标准差S1(式(10))评估了上述计算方法的预测精度。经典欧拉公式[9](式(1))的A1和S1分别为17.3%和21.4%,其A2为115.9%,意味着欧拉公式高估了FRP构件弯曲屈曲临界力约15.9%。由于考虑了剪切变形的影响,Engesser[13]和Haringx[15]修正公式(式(3)、(4))在经典欧拉公式的基础上考虑了剪切变形对FRP构件屈曲临界力的影响,其预测精度比欧拉公式稍高,分别高估了FRP构件弯曲屈曲临界力约9.4%和10.1%。Strongwell公司[17]建议的经验公式(式(5))高估了FRP构件弯曲屈曲临界力约160.4%,且A1和S1分别高达161.6%和130.5%。如此大的预测误差使得Strongwell公司建议公式并不可靠,不能用于FRP构件弯曲屈曲临界力的预测。Fiberline公司[18]建议的经验公式(式(6))低估了FRP构件弯曲屈曲临界力约8.6%。
| 表 3 FRP轴压构件弯曲屈曲临界力的不同计算方法预测精度比较 Tab. 3 Comparison of prediction accuracy of different calculation methods for flexural buckling loads of axially loaded FRP members |
| $ A_1=\frac{\sum\limits_{i=1}^n\left|\frac{p_i-e_i}{e_i}\right|}{n} $ | (8) |
| $ A_2=\frac{\sum\limits_{i=1}^n \frac{p_i}{e_i}}{n} $ | (9) |
| $ S_1=\sqrt{\frac{\sum\limits_{i=1}^n\left(\frac{p_i}{e_i}-A_2\right)^2}{n}} $ | (10) |
式中:pi为第i个预测值,ei为第i个试验值,n为样本总数。
4 FRP轴压构件弯曲屈曲临界力的新计算方法为了推导FRP轴心受压构件弯曲屈曲临界力的计算方法,做如下假设:
1) FRP型材是均质、线弹性及正交各向异性的材料;
2) FRP构件截面厚度方向的剪应力及剪应变可忽略;
3) 与FRP构件纵向的应力相比,其他两个方向的应力非常小,可以忽略;
4) FRP构件在轴心压力作用下变形属于小变形范畴。
根据Mottram等[11]可知,目前还没有研究成果表明残余应力会影响FRP构件的稳定性能,因此,假设FRP构件的缺陷仅包含初始弯曲。
轴压构件整体稳定系数(χ)即构件压缩应力与材料抗压强度的比值可通过式(11)[34]得到。
| $ \begin{gathered} \sigma_{\mathrm{cr}}=\frac{F_{\mathrm{LC}}+\left(1+\varepsilon_0\right) \sigma_{\mathrm{E}}}{2}- \\ \sqrt{\left(\frac{F_{\mathrm{LC}}+\left(1+\varepsilon_0\right) \sigma_{\mathrm{E}}}{2}\right)^2-F_{\mathrm{LC}} \sigma_{\mathrm{E}}} \end{gathered} $ | (11) |
其中
| $ \sigma_{\mathrm{E}}={\rm{ \mathit{π} }}^2 E_{\mathrm{LC}} / \lambda^2 $ | (12) |
| $ \varepsilon_0=v_0 A_{\mathrm{g}} / S $ | (13) |
式(11)整理可得
| $ \chi=\frac{\sigma_{\mathrm{cr}}}{F_{\mathrm{LC}}}=\frac{\left(1+\varepsilon_0+\lambda_{\mathrm{n}}^2\right)-\sqrt{\left(1+\varepsilon_0+\lambda_{\mathrm{n}}^2\right)^2-4 \lambda_{\mathrm{n}}^2}}{2 \lambda_{\mathrm{n}}^2} $ | (14) |
其中
| $ \lambda_{\mathrm{n}}=(\lambda / {\rm{ \mathit{π} }}) \sqrt{F_{\mathrm{LC}} / E_{\mathrm{LC}}} $ | (15) |
式中:σcr为弯曲屈曲临界应力,σE为欧拉屈曲临界应力,ε0为FRP构件相对初始弯曲,υ0为FRP构件长度中点处的初始挠度,λn为通用长细比。FRP构件的弯曲屈曲临界力可采用式(16)进行计算。
| $ P_\chi=\chi F_{\mathrm{LC}} A_{\mathrm{g}} $ | (16) |
式中Pχ为采用轴压构件整体稳定系数(χ)计算的FRP构件的弯曲屈曲临界力。
式(16)为中国钢结构设计标准[19]及欧洲钢结构设计标准[20]用于计算钢构件整体屈曲临界力的计算式。对于FRP构件,需给出FRP构件相对初始弯曲(ε0)的准确表达式,才能使用式(16)预测FRP构件弯曲屈曲临界力。
由GB 50018—2002《冷弯薄壁型钢结构技术规范》[35]可知,相对初始弯曲可假设为式(17)的形式。
| $ \varepsilon_0=A+B \lambda_{\mathrm{n}}^2 $ | (17) |
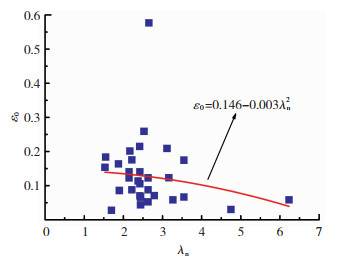
根据Zureick等[28]、Lane等[6]以及Mottram等[11]给出的FRP试验构件长度中点处的初始挠度(υ0)实测值,给出了FRP构件相对初始弯曲(ε0)与通用长细比(λn)之间的变化关系,见图 3。通过最小二乘法的回归分析,得到式(17)中的系数A和B分别为0.146和-0.003。将式(17)带入式(14)可以得到FRP构件整体稳定系数(χ)表达式:
| $ \chi=\frac{\sigma_{\mathrm{cr}}}{F_{\mathrm{LC}}}=\frac{1.15+\lambda_{\mathrm{n}}^2-\sqrt{\left(1.15+\lambda_{\mathrm{n}}^2\right)^2-4 \lambda_{\mathrm{n}}^2}}{2 \lambda_{\mathrm{n}}^2} $ | (18) |
|
图 3 FRP构件相对初始弯曲和通用长细比的关系 Fig. 3 Variation of relative initial crookedness with universal slenderness ratio |
图 4为数据库中所有FRP试验构件的稳定系数随通用长细比变化的情况。通过对176根FRP构件试验数据的回归分析,给出了计算FRP轴压构件弯曲屈曲临界力的经验公式(式(19))。
| $ P_{\mathrm{z}}=\frac{P_{\mathrm{E}}}{1+0.04 \sqrt{\beta P_{\mathrm{E}} /\left(G_{\mathrm{LT}} A_{\mathrm{g}}\right)}+P_{\mathrm{E}} /\left(2 N_{\mathrm{C}}\right)} $ | (19) |

|
图 4 试验数据及式(19)曲线 Fig. 4 Test data and curve of Eq.(19) |
式中Pz为本文模型计算的屈曲临界力,PE、β和NC的物理意义与式(3)和(7)相同。由于式(19)是以数据库中试验数据为基础回归得到的经验公式,因此也间接考虑了FRP构件初始缺陷对其弯曲屈曲临界力的影响。
4.1 理论计算模型的验证通过对比数据库中不同截面形状的FRP轴压构件弯曲屈曲临界力的试验值与预测值,可验证由FRP构件初始弯曲表达式(式(17))推导得到的FRP构件整体稳定系数表达式(式(18))的正确性,以及以式(18)作为整体稳定系数表达式并采用式(16)计算考虑初始几何缺陷影响的FRP构件弯曲屈曲临界力的预测精度。
选择数据库中宽翼缘和普通翼缘工字形截面、L形截面、方管及圆管共5组FRP构件的试验数据,每组6根构件,且截面尺寸不同,见表 4。由于FRP构件初始弯曲表达式(式(17))对于稳定系数表达式(式(18))及弯曲屈曲临界力的计算式(式(16))而言是最重要的参数之一,因此,用于推导FRP构件初始弯曲表达式中系数A和B所用的试验数据并未包含在表 4中。
| 表 4 FRP轴压构件及其弯曲屈曲临界力试验值与预测值 Tab. 4 Typical FRP members and flexural buckling loads from tests and predictions |
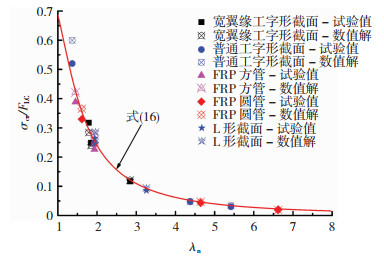
表 4和图 5给出上述30根FRP构件试验值与式(16)预测值的比较。从图 5可看出试验值与式(16)的曲线吻合较好。从表 4可看出式(16)对于上述30根FRP构件弯曲屈曲临界力的预测误差在-10.0%~13.2%。式(16)的A1和S1分别为6.8%和6.7%,其A2为104.2%,这说明式(16)高估了FRP构件弯曲屈曲临界力约4.2%。因此,与试验值相比,式(16)给出了精度相对较高的FRP轴压杆件弯曲屈曲临界力的预测值,同时也间接验证了FRP构件初始弯曲表达式(式(17))以及FRP构件稳定系数表达式(式(18))的合理性。
|
图 5 FRP轴压构件弯曲屈曲试验值、数值解及式(16)曲线的比较 Fig. 5 Comparison between curve of Eq.(16) and test and numerical results of axially loaded FRP specimens |
FRP轴压构件弯曲屈曲临界力的经验公式(式(19))是基于数据库中176根FRP构件试验数据的回归分析得到,若采用数据库中的试验数据进行验证没有意义。本文利用有限元软件ANSYS进行一批新试件的数值计算,采用这批新试件的数值计算结果验证式(19)。在此之前,首先通过对比数据库中试件的有限元模型计算结果与试验结果验证有限元建模的准确性。
采用ANSYS[36]建立了FRP构件的有限元模型。按照不同的构件截面和FRP材料进行建模计算,选择的构件截面包含了工字形截面(宽翼缘及普通工字形截面)、矩形截面、圆形截面及L形截面共4类截面。模型中假设FRP构件是线弹性及正交各向异性材料,相应的几何尺寸及材料基本力学性能见表 4。FRP构件采用SHELL63单元模拟。SHELL63单元是4节点的板壳单元,每个节点6个自由度,可用来模拟具有线弹性特性的正交各向异性薄壁构件[37-39]。根据FRP构件的截面形状及尺寸,将截面划分为8~24个单元,沿轴向的网格划分根据构件长度不同将单元的长宽比控制在1.7 ∶1~2 ∶1,以保证数值计算的精度[40]。试件W1的数值模型及网格划分情况见图 6。

|
图 6 FRP轴压构件的数值模型、网格划分及失效模式 Fig. 6 Finite element modeling, mesh, and failure modes of typical FRP members |
根据试验中实际的约束情况及有限元程序中SHELL63单元的特性,约束FRP构件模型底部截面X和Z方向的平动自由度,而Y方向的平动自由度只约束底部截面中的一个或两个节点。对于FRP构件模型顶部截面,只约束其X和Z方向的平动自由度。FRP构件弯曲屈曲临界力的数值解(表 4)通过特征值屈曲分析和非线性屈曲分析得到。特征值屈曲分析忽略了构件初始几何缺陷对屈曲临界力的影响。然而FRP试验构件实际的几何缺陷是未知的,因此,通常在数值分析中设置合理的缺陷值代替实测值。在实际构件中,通过拉挤工艺得到的FRP构件的初始弯曲模式有4种[6, 11, 28](图 7),在有限元模拟中选取一种最具代表性的初弯曲模式,参考钢构件,选取图 7中的第一种初始弯曲模式,同时采用1‰、2‰、3‰、4‰和5‰构件长度共5个初始缺陷进行数值计算,结果显示取1‰构件长度作为初始缺陷时,有限元模拟的结果与试验结果最为接近,说明在有限元模拟中,FRP压杆模型的初始弯曲模式取图 7中的第一种,且取1‰构件长度作为初始缺陷,能大致代表数据库中FRP构件初始弯曲的平均水平。因此,在有限元模拟中取1‰构件长度作为初始缺陷进行计算。具体施加步骤如下:1)进行特征值屈曲分析,得到轴压构件的一阶屈曲模态;2)进行非线性屈曲分析,利用“UPGEOM”命令将特征值屈曲分析得到的一阶屈曲模态形状的1‰作为初始缺陷施加在轴压杆件的模型上。若FRP轴压构件的截面尺寸及有效长度超出了数据库的范围,则取1‰构件长度作为初始缺陷需要进一步验证。

|
图 7 FRP构件的4种实测初弯曲模式[6, 11, 28] Fig. 7 Four measured initial crookedness modes of FRP members[6, 11, 28] |
数值计算得到的表 4中试件W1、I1、S1、R1和L1的失效模式见图 6。表 4中其余试件的失效模式与同截面形状上述试件的失效模式基本相同,均为弯曲屈曲失效。即数值计算得到的与试验得到的FRP构件失效模式基本一致,均为弯曲屈曲。同时,表 4中30根FRP构件弯曲屈曲临界力的数值计算值与试验值也进行了比较。从表 4可看出,数值计算值的A1和S1分别为8.9%和8.2%,其A2为105.4%,说明数值计算高估了FRP构件弯曲屈曲临界力约5.4%。这也说明数值计算可以相对较好地预测FRP构件弯曲屈曲临界力。
表 5给出了不在数据库中的宽翼缘和普通翼缘工字形截面、L形截面、方管及圆管共5组30根FRP构件的截面尺寸,计算长度及基本材性数据。上述FRP构件并未经过轴压试验测试。表 5同时给出了上述30根FRP构件弯曲屈曲临界力的数值计算解和式(19)的预测值,其中数值计算所采用的模型是前述被验证过的数值模型。以数值计算解为基准,式(19)预测值的A1和S1分别为8.3%和7.7%,其A2为95.4%,意味着式(19)低估了FRP构件弯曲屈曲临界力数值计算解约4.6%。考虑到前述通过与试验结果对比得到的数值解高估了试验值约5.4%,可以推得式(19)高估了FRP构件弯曲屈曲临界力试验值约0.8%,预测精度较高,这也初步验证了式(19)预测FRP构件弯曲屈曲临界力的有效性及精度。
| 表 5 FRP轴压构件及其弯曲屈曲临界力预测值 Tab. 5 Axially loaded FRP members and predicted flexural buckling loads |
图 4和图 8分别给出了式(19)和式(16)的曲线以及数据库中所有FRP构件的试验值。为了进一步研究式(16)、式(19)的预测精度,以数据库中试验数据为依据,将既有计算方法与新计算方法同时进行对比分析(图 2)。式(16)曲线与Engesser[13]和Haringx[15]修正公式的曲线比较接近,但位于上述两曲线的下方,这也说明式(16)对于FRP构件弯曲屈曲临界力的预测精度稍高于Engesser[13]和Haringx[15]修正公式。虽然不同FRP构件初弯曲的数据点离散性相对较大(图 3),但式(16)的预测精度仍高于既有的5种预测方法,这说明与未考虑初始弯曲影响的既有5种预测方法相比,式(16)通过考虑FRP构件初始弯曲的影响提高了对其弯曲屈曲临界力的预测精度。同时,由于FRP型材4种初始弯曲模式的存在,使得初弯曲表达式(式(17))及式(16)仍有修正空间。由图 8(b)可知,在通用长细比较小(0.5 < λn < 1.0)时,式(16)预测误差增加。这是由于当通用长细比降低到一定范围(λn < 1.0)时,FRP轴压构件的整体屈曲临界力与局部屈曲临界力比较接近甚至相等,FRP轴压构件将会发生整体屈曲与局部屈曲耦合的情况,即耦合屈曲,其屈曲临界力与整体屈曲和局部屈曲临界力差异较大。由于式(19)是通过数据库给出的经验公式,因此,式(19)在图中表现出最好的预测精度也在情理之中。然而图 2中式(19)与式(1)、(3)、(4)、(6)和(16)的关系也间接验证了式(19)的预测精度。

|
图 8 试验数据及式(16)曲线 Fig. 8 Test data and curve of Eq.(16) |
由既有计算方法与新计算方法对于数据库中176根FRP轴压构件弯曲屈曲临界力预测情况的统计(表 2)可知,式(16)和式(19)的预测误差相对较小,其A1均约为10%。式(16)高估了FRP构件弯曲屈曲临界力约4.2%,式(19)的预测值与试验值更为接近,仅高估了FRP构件弯曲屈曲临界力约0.8%。Engesser[13]和Haringx[15]修正公式在经典欧拉公式的基础上考虑了剪切变形对FRP构件屈曲临界力的影响。式(16)则进一步考虑了构件初始几何缺陷对稳定性能的影响。尽管式(19)是以数据库为基础给出的经验公式,但也间接考虑了剪切变形以及初始几何缺陷对构件屈曲临界力的影响。式(16)和(19)以相对较好的预测精度以及相对简单的计算式的构成,适合用于包含FRP轴压构件的结构设计。
6 结论基于所建立的包含176根FRP轴压构件弯曲屈曲失效试验数据的数据库,评价了既有的5种计算方法,提出了两种预测FRP轴压构件弯曲屈曲临界力新的计算方法并进行了验证及评价,得到以下结论:
1) 经典欧拉公式高估了FRP构件弯曲屈曲临界力,平均绝对误差约为17.3%。由于考虑了剪切变形的影响,Engesser和Haringx修正公式的预测精度明显优于欧拉公式,虽然也高估了FRP构件弯曲屈曲临界力,但平均绝对误差有所降低。
2) Fiberline公司建议公式是既有计算方法中唯一保守的方法,低估了FRP构件弯曲屈曲临界力约8.6%。Strongwell公司建议公式由于其过大的预测误差,不建议用于FRP构件弯曲屈曲临界力的预测。
3) 本文提出的FRP构件的整体稳定系数计算公式(式(18))考虑了FRP构件几何初始缺陷的影响,将其带入式(16)后,其预测精度明显优于既有5种预测方法。经验公式(式(19))考虑了FRP构件初始缺陷及剪切变形的影响,其预测精度最高。式(16)和(19)以相对较好的预测精度以及相对简单和熟悉的计算式构成,适合用于包含FRP轴压构件的结构设计。
上述结论是以176根FRP轴压构件的弯曲屈曲试验数据的数据库为基础得到,若FRP轴压构件的截面尺寸及有效长度超出了数据库的范围,则结论需进一步验证。同时针对数据库中普通工字形截面和L形截面FRP构件研究相对较少的情况,后续将通过新一批的普通工字形截面和L形截面FRP轴压构件的试验数据进一步验证所提模型的预测性能。
| [1] |
HOLLAWAY L C. A review of the present and future utilization of FRP composites in the civil infrastructure with reference to their important in-service properties[J]. Construction and Building Materials, 2010, 24(12): 2419. DOI:10.1016/j.conbuildmat.2010.04.062 |
| [2] |
KELLER T. Fibre reinforced polymer materials in building construction[C]//Proceedings of IABSE Symposium. Melbourne: IABSE, 2002: 73. DOI: 10.2749/222137802796335136
|
| [3] |
叶列平, 冯鹏. FRP在工程结构中的应用与发展[J]. 土木工程学报, 2006, 39(3): 24. YE Lieping, FENG Peng. Applications and development of fiber-reinforced polymer in engineering structures[J]. China Civil Engineering Journal, 2006, 39(3): 24. DOI:10.15951/j.tmgcxb.2006.03.004 |
| [4] |
ZHAN Y, WU G, YANG L S. Experimental investigation of the behavior of a lattice steel column repaired with pultruded GFRP profiles[J]. Journal of Performance of Constructed Facilities, ASCE, 2015, 29(4). DOI:10.1061/(ASCE)CF.1943-5509.0000600 |
| [5] |
CORREIA M M, NUNES F, CORREIA J R, et al. Buckling behavior and failure of hybrid fiber-reinforced polymer pultruded short columns[J]. Journal of Composites for Construction, ASCE, 2013, 17: 463. DOI:10.1061/(ASCE)CC.1943-5614.0000339 |
| [6] |
LANE A, MOTTRAM J T. Influence of modal coupling on the buckling of concentrically loaded pultruded fibre-reinforced plastic columns[J]. Proceedings of the Institution of Mechanical Engineers, Part L: Journal of Materials: Design and Applications, 2002, 216(2): 133. DOI:10.1243/146442002320139333 |
| [7] |
BARBERO E J. Prediction of buckling-mode interaction in composite columns[J]. Mechanics of Composite Materials and Structures, 2000, 7: 269. DOI:10.1080/10759410050031130 |
| [8] |
HASHEM Z A, YUAN R L. Short vs. long column behavior of pultruded glass-fiber reinforced polymer composites[J]. Construction and Building Materials, 2001, 15(8): 369. DOI:10.1016/S0950-0618(01)00018-6 |
| [9] |
ZIEMIAN D R. Guide to stability design criteria for metal structures[M]. 6th ed. Hoboken: John Wiley & Sons, Inc., 2010: 23.
|
| [10] |
ZUREICK A. FRP pultruded structural shapes[J]. Progress in Structural Engineering and Materials, 1998, 1(2): 143. DOI:10.1002/pse.2260010206 |
| [11] |
MOTTRAM J T, BROWN N D, ANDERSON D. Physical testing for concentrically loaded columns of pultruded glass fibre reinforced plastic profile[J]. Proceedings of the Institution of Civil Engineers-Structures and Buildings, 2003, 156(2): 205. DOI:10.1680/stbu.2003.156.2.205 |
| [12] |
BANK L C. Composites for construction: structural design with FRP materials[M]. Hoboken: Wiley, 2006.
|
| [13] |
ENGESSER F. Vber die Knickfestigkeit gerader Stäbe[J]. Zeitschrift für Architektur und Ingenieurwesen, 1889, 35(4): 455. |
| [14] |
KARDOMATEAS G A, DANCILA D S. Buckling of moderately thick orthotropic columns: comparison of an elasticity solution with the Euler and Engesser/Haringx/Timoshenko formulae[J]. International Journal of Solids and Structures, 1997, 34(3): 341. DOI:10.1016/S0020-7683(96)00020-0 |
| [15] |
HARINGX J A. On highly compressible helical springs and rubber rods, and their application for vibration-free mountings[R]. Eindhoven: [s. n. ], 1948
|
| [16] |
BARBERO E J, DEVIVO L. Beam-column design equations for wide-ange pultruded structural shapes[J]. Journal of Composites for Construction, ASCE, 1999, 3(4): 185. DOI:10.1061/(ASCE)1090-0268(1999)3:4(185) |
| [17] |
Strongwell Corporation. Strongwell design manual[S]. Bristol: Strongwell Corporation, 2013
|
| [18] |
Fiberline Composites. Fiberline design manual[S]. Fredericia: Fiberline Composites A/S, 2003
|
| [19] |
钢结构设计标准: GB 50017—2017[S]. 北京: 中国建筑工业出版社, 2017 Code for design of steel structure: GB 50017—2017[S]. Beijing: China Architecture & Building Press, 2017 |
| [20] |
Eurocode 3: design of steel structures-part 1-1: general rules and rules for buildings[S]. Brussels: [s. n. ], 2005
|
| [21] |
BARBERO E J, TOMBLIN J. Euler buckling of thin-walled composite columns[J]. Thin-Walled Structures, 1993, 17: 237. DOI:10.1016/0263-8231(93)90005-U |
| [22] |
BARBERO E J, TROVILLION J. Prediction and measurement of the post-critical behavior of fiber ber-reinforced composite columns[J]. Composites Science and Technology, 1998, 58(8): 1335. DOI:10.1016/S0266-3538(98)00006-2 |
| [23] |
SEANGATITH S, SRIBOONLUE W. Axially loaded glass-fiber reinforced plastic composite columns[C]// Proceedings of the Seventh East Asia-Pacific Conference on Structural Engineering and Construction (EASEC-7). Kochi: [s. n. ], 1999, 1307
|
| [24] |
WOOD J. Structural design of polymer composites EUROCOMP design code and handbook[J]. Composite Structures, 1996, 35(4): 445. DOI:10.1016/S0263-8223(96)00058-X |
| [25] |
Bedford Reinforced Plastics Inc. Bedford design guide[S]. Bedford: Bedford Reinforced Plastics Inc., 2010
|
| [26] |
Creative Pultrusions Inc. The Pultex pultrusion global design manual of standard and custom fiber reinforced polymer structural profiles[S]. Pennsylvania: Creative Pultrusions Inc., 2004
|
| [27] |
RICHARDS T H, STANLEY P. Stability problems in engineering structures and components[M]. New York: Elsevier Applied Science, 1978: 23.
|
| [28] |
ZUREICK A, SCOTT D. Short-term behavior and design of fiber-reinforced polymeric slender members under axial compression[J]. Journal of Composites for Constructions, ASCE, 1997, 140. DOI:10.1061/(ASCE)1090-0268(1997)1:4(140) |
| [29] |
ROBERTS T M. Influence of shear deformation on buckling of pultruded fiber reinforced plastic profiles[J]. Journal of Composites for Constructions, ASCE, 2002, 6(4): 241. DOI:10.1061/(ASCE)1090-0268(2002)6:4(241) |
| [30] |
VANEVENHOVEN L M, SHIELD C K, BANK L C. LRFD factors for pultruded wide-flange columns[J]. Journal of Structural Engineering, ASCE, 2010, 136(5): 554. DOI:10.1061/(ASCE)ST.1943-541X.0000126 |
| [31] |
BOSCATO G, CASALEGNO C, RUSSO S, et al. Buckling of built-up columns of pultruded fiber-reinforced polymer C-sections[J]. Journal of Composites for Constructions, ASCE, 2014, 04013050. DOI:10.1061/(ASCE)CC.1943-5614.0000453 |
| [32] |
PUENTE I, INSAUSTI A, AZKUNE M. Buckling of GFRP columns: an empirical approach to design[J]. Journal of Composites for Constructions, ASCE, 2006, 10(6): 529. DOI:10.1061/(ASCE)1090-0268(2006)10:6(529) |
| [33] |
LEE S, CHAE S H, YOON S J, et al. A study on the design curves for pultruded composite columns[J]. Advanced Materials Research, 2007, 26/27/28: 337. |
| [34] |
AYRTON W E, PERRY J. On struts[M]. London: The Engineer, 1866: 464.
|
| [35] |
冷弯薄壁型钢结构技术规范: GB 50018—2002[S]. 北京: 中国建筑工业出版社, 2002 Technical code of cold-formed thin-wall steel structures: GB 50018—2002[S]. Beijing: China Architecture & Building Press, 2002 |
| [36] |
ANSYS Inc.. ANSYS user's manual, release 10.0.[M]. Canonsburg: ANSYS Inc., 2009.
|
| [37] |
QIAO P Z, DAVALOS J F, WANG J L. Local buckling of composite FRP shapes by discrete plate analysis[J]. Journal of Structural Engineering, ASCE, 2001, 127(3): 245. DOI:10.1061/(ASCE)0733-9445(2001)127:3(245) |
| [38] |
QIAO P Z, ZOU G P. Local buckling of composite fiber-reinforced plastic wide-flange sections[J]. Journal of Structural Engineering, ASCE, 2003, 129(1): 125. DOI:10.1061/(ASCE)0733-9445(2003)129:1(125) |
| [39] |
FAM A, KIM Y J. Numerical analysis of pultruded GFRP box girders supporting adhesively-bonded concrete deck in flexure[J]. Engineering Structures, 2011, 33(12): 3527. DOI:10.1016/j.engstruct.2011.07.016 |
| [40] |
TURVEY G J, ZHANG Y. A computational and experimental analysis of the buckling, postbuckling and initial failure of pultruded GRP columns[J]. Computers and Structures, 2006, 84(22/23): 1527. DOI:10.1016/j.compstruc.2006.01.028 |
| [41] |
NUNES F, CORREIA M, CORREIA J R, et al. Experimental and numerical study on the structural behavior of eccentrically loaded GFRP columns[J]. Thin-Walled Structures, 2013, 72: 175. DOI:10.1016/j.tws.2013.07.002 |
| [42] |
CARDOSO D C T, HARRIES K A, BATISTA E M. Compressive strength equation for GFRP square tube columns[J]. Composites Part B: Engineering, 2014, 59: 1. DOI:10.1016/j.compositesb.2013.10.057 |
| [43] |
王虎长, 胡建民, 赵雪灵. 玻璃钢复合材料轴压构杆稳定性分析[J]. 电力建设, 2011, 32(9): 85. WANG Huchang, HU Jianmin, ZHAO Xueling. Stability analysis of axial compression component of FRP[J]. Electric Power Construction, 2011, 32(9): 85. DOI:10.3969/j.issn.1000-7229.2011.09.021 |
| [44] |
ZUREICK A, STEFFEN R. Behavior and design of concentrically loaded pultruded angle struts[J]. Journal of Structural Engineering, ASCE, 2000, 126(3): 406. DOI:10.1061/(ASCE)0733-9445(2000)126:3(406) |
| [45] |
张兴虎, 马贵斌, 冯海潮. FRP等边角材轴心受压构件的试验研究[J]. 玻璃钢/复合材料, 2011, 4: 51. ZHANG Xinghu, MA Guibin, FENG Haichao. Experimental research of fiber reinforced plastics equal angle axial compression members[J]. Fiber Reinforced Plastic/Composites, 2011, 4: 51. |
| [46] |
GODAT A, LÉGERON F, GAGNÉ V, et al. Use of FRP pultruded members for electricity transmission towers[J]. Composite Structures, 2013, 105: 408. DOI:10.1016/j.compstruct.2013.05.025 |
 2023, Vol. 55
2023, Vol. 55


