钢筋混凝土(RC)框架结构具有使用空间灵活、造价低、耐久性好等优点, 是多、高层建筑中常见的结构体系。震害现象表明[1], 严格按照规范设计和施工的RC框架结构在经历超出设防烈度的地震作用后,尽管可以满足“大震不倒”的抗震设防目标, 但往往在梁端及底层柱端产生较大的塑性变形, 震后修复困难, 甚至发生超出设计预期的严重破坏, 造成巨大的财产损失和人员伤亡[2]。传统现浇RC框架以及在等效现浇理念下常用的湿式连接装配式RC框架, 由于其施工效率低, 施工质量不易保证, 不能满足建筑工业化和可持续发展的要求[3]。
装配式建筑是实现建筑工业化的有效途径。装配式构件间的连接节点及连接构造将直接影响装配式建筑的施工效率、造价、抗震性能、震后可修复性等, 也是其推广应用的关键。装配式RC框架结构的连接节点主要包括预制梁与柱以及预制柱之间的连接节点, 国内外学者已经开展了很多富有成效的研究。
关于梁柱之间连接的研究成果及工程应用较多[4-6], 而预制柱间的连接方式[7-12]及装配式框架结构体系[13-14]的相关研究相对较少。文献[15]提出一种新型可更换消能柱脚和RC柱组成的装配式组合柱, 通过对8个试件的低周往复加载试验, 重点研究可更换钢板面积、轴压比和填充块材料对组合柱抗震性能和可更换性能的影响。李春雨等[16]为评估带有可更换耗能连接的装配式混凝土框架(REDC-PCF)的抗震性能, 设计并制作了1榀2层2跨带有可更换耗能连接的装配式混凝土框架缩尺试件, 对其开展拟静力试验, 试验得到的滞回曲线饱满且稳定, 呈现出优异的抗震性能。刘阳等[17]提出一种适用可更换组合柱, 验证了核心方钢管锚固地梁的可更换构造具有更高的承载力和耗能能力。罗青儿等[18]对6根纵筋采用套筒连接带钢管混凝土榫头的装配柱进行了试验, 认为这种装配式结构榫式接头柱施工方便且受力可靠, 可用于实际工程。汪梅等[19-20]对5根足尺的齿槽+钢板焊接的装配式结构柱进行了试验研究, 证明了装配式结构柱采用焊接连接的可靠性, 试件破坏时钢板屈服, 节点延性和受力性能良好, 表现出良好的抗震性能。郑先超等[8-10]提出采用外包钢板+螺栓杆的柱间连接方式, 对比分析了现浇柱和高强箍筋约束装配柱的拟静力试验结果, 认为装配柱与现浇柱的抗震性能相同, 耗能能力良好, 装配式结构柱连接节点处的屈服和破坏荷载、滞回耗能均优于现浇柱。
本文提出一种传力明确、施工构造简单的新型全装配式RC柱间可更换耗能节点(new fully precast RC column with replaceable energy consulting joints, RECJ)型式, 将该连接型式用于RC框架结构破坏严重的底层柱, 设计制作两个RECJ连接装配式底层柱和一个现浇RC对比柱。通过对3个试件进行拟静力试验研究, 考察并评价试件的破坏形态、滞回曲线及骨架曲线、刚度和承载力退化、延性及耗能、钢板及钢筋应力变化等性能。
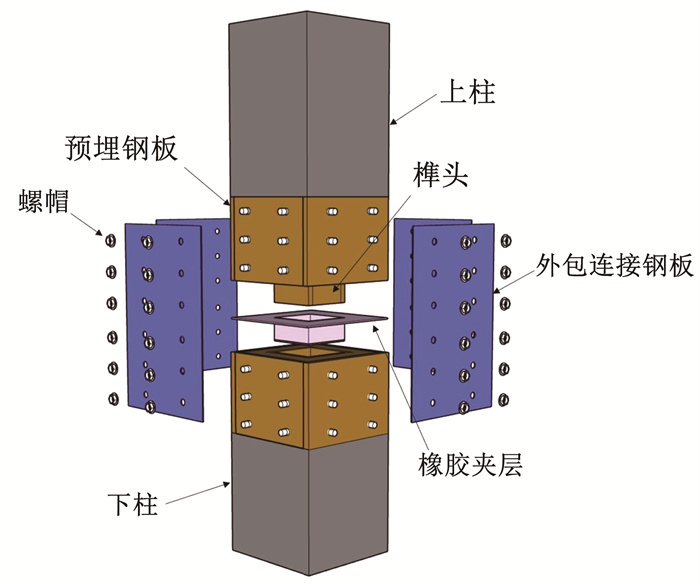
1 预埋螺栓钢板连接节点构造提出的新型“榫卯+连接钢板”全装配式RC柱间RECJ示意见图 1。连接节点处主要由上柱、下柱、耗能连接钢板、预埋连接螺栓及预埋构造加强钢板等部件组成。连接节点处上柱下端为凸出榫头, 下柱上端为凹口, 二者形成榫卯连接, 为了防止接触面的挤压和碰撞, 在其间隙填充氯丁橡胶。柱身外包的预埋构造钢板在施工时控制预埋螺栓位置, 加载时保护连接部位混凝土避免局部破坏。耗能连接钢板通过预制柱身预埋的螺栓将上、下柱连为整体。采用RECJ连接的装配柱制作工厂化程度高, 现场施工简便, 为了使损伤集中在连接处, 在设计时耗能连接钢板的承载力和刚度弱于其他部分, 钢板在受力后首先屈曲耗能, 最大限度地保证预制构件和结构的安全, 有利于结构震后的快速修复。且由于震后主体结构一直处于弹性, 只需更换损伤的连接钢板既可以快速恢复建筑的使用功能。
|
图 1 RECJ柱连接节点构造示意 Fig. 1 Schematic diagram of connection node details of RECJ column |
将RECJ节点用于某设防烈度为8度地区的7层现浇RC框架结构底层柱, 柱高为5.4 m。设计制作了3个1/2缩尺试验模型, 其中两个为新型装配柱(编号分别为RECJZ1、RECJZ2), 另一个为现浇RC框架对比柱(编号XJZ), 将RECJZ2试件加载至1/25的层间位移角后更换受损连接板重新加载(编号RECJZ2-C)。3个试件的截面尺寸均为400 mm× 400 mm, 试验加载的水平合力点距地梁顶面1.8 m。此处假定底层柱的反弯点位于2/3柱高度处, 即2/3×(1/2×5.4)=1.8 m, 剪跨比为4.5, 试验轴压比为0.3。纵筋和箍筋均采用HRB400级热轧带肋钢筋。3个试件纵筋均为对称配置8 22, 箍筋为10@100复合箍筋。为便于工人施工安装及受力, 试件RECJZ1、RECJZ2的节点位于距基础顶面500 mm处。两个装配试件的榫头长度分别为100、200 mm, 连接钢板为Q235钢, 厚度为4 mm, 螺孔直径为24 mm, 预埋螺栓为M22的10.9级承压型高强螺栓。为了保证接头连接部位及柱脚强度, 预制构件连接部位及柱脚外包3 mm厚加强钢板, 并在柱脚处将钢板用螺栓与地梁进行锚固。现浇试件XJZ和装配式结构柱试件RECJZ1的构造及截面如图 2所示, 试件RECJZ2与RECJZ1区别仅为榫头长度由100 mm变更为200 mm。试件的主要设计参数见表 1。

|
图 2 试件尺寸及构造详图 Fig. 2 Geometrical dimensions and details of specimens |
| 表 1 试件参数 Tab. 1 Parameters of specimens |
分别按照材性测试标准要求留取、制作标准混凝土和钢材的材性测试试件并进行试验[21-22]。混凝土立方体标准试件的入模及养护作到与试验试件同时入模、同条件养护28 d, 测得混凝土立方体抗压强度为62.3 MPa。钢材的力学性能见表 2。
| 表 2 钢材力学性能 Tab. 2 Mechanical properties of steel |
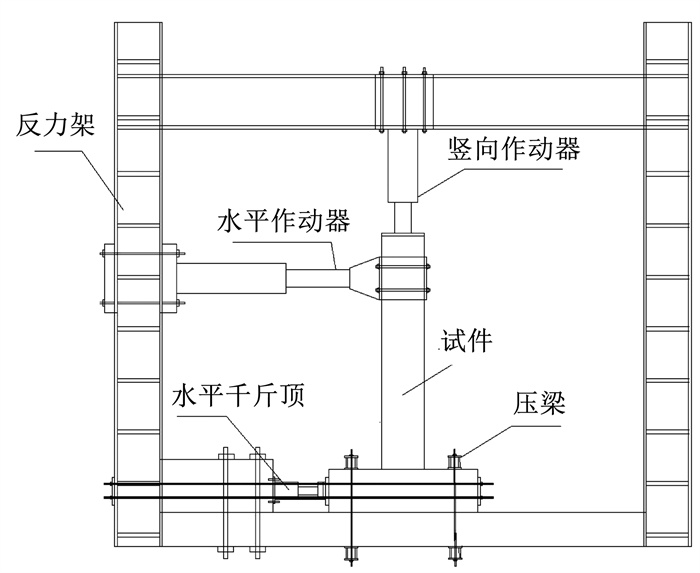
试件加载装置及量测方案分别如图 3和4所示。试验时将试件底梁利用压梁及千斤顶与反力架固定, 分别采用100、200 t的邦威电液伺服加载系统进行柱端水平向低周往复试验及柱顶的轴向加载。
|
图 3 加载示意 Fig. 3 Test setup diagram |
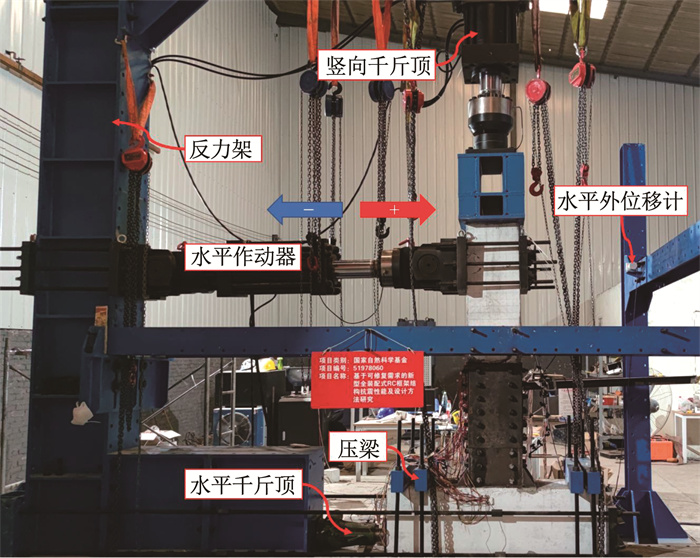
|
图 4 实际加载装置 Fig. 4 Actual test setup |
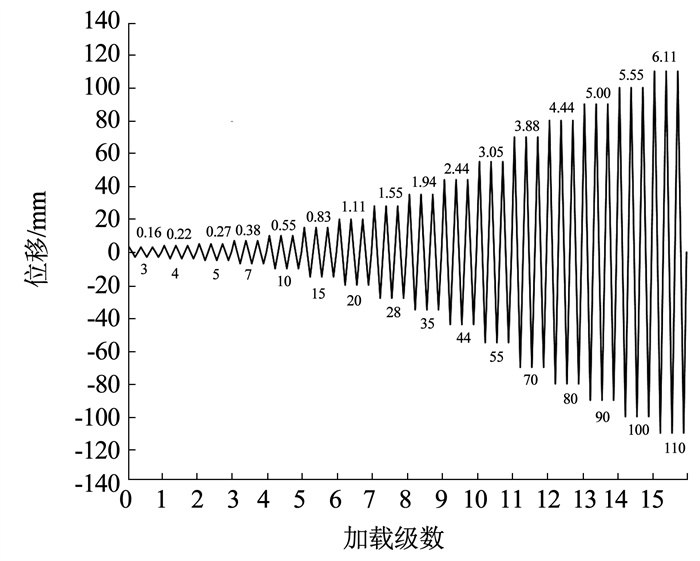
采用竖向液压千斤对柱顶一次性施加1 824 kN轴向压力, 并在整个试验过程中保持不变。水平向加载采用位移控制, 在正式加载前, 进行加载位移为1、2 mm的预加载, 每级加载一次, 以检验系统是否正常工作。加载制度如图 5所示[23], 正式加载的位移角分别为0.16%、0.22%、0.27%、0.38%、0.55%、0.83%、1.11%、1.55%、1.94%、2.44%、3.05%、3.88%和4.44%等, 每级循环3次, 直到承载力下降至最大承载力的85%时判定试件完全破坏, 停止加载。
|
图 5 加载制度 Fig. 5 Loading protocol of horizontal load |
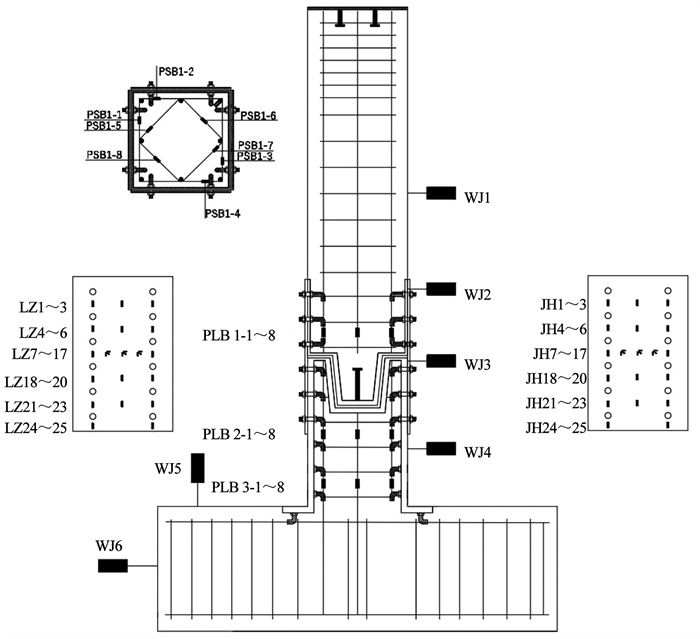
试验过程中, 位移和力分别通过外位移计和作动器自带力传感器采集, 在钢板和钢筋上布置3 mm× 3 mm的电阻应变片。为了测定试验过程中现浇节点和装配式节点的钢筋应变, 在节点核心区、企口的拼接处布置应变片, 如图 6所示, 在连接钢板处布置应变片, 通过应变分析试件的受力性能。
|
图 6 应变片布置 Fig. 6 Strain arrangement |
试件XJZ在水平负向加载位移达到3 mm(加载力为214 kN)时, 距柱脚200 mm高处开始出现宽度为0.1 mm的水平及斜向裂缝, 水平裂缝宽度随位移角的增加进一步发展, 且新裂缝数量也不断增加。裂缝随加载逐渐向斜上方发展延伸至柱截面中部, 相互交联形成柱表面的主要裂缝。加载位移至28 mm时, 试件达到极限承载力354.6 kN。加载位移至44 mm(加载力为301.6 kN)时, 左侧柱脚混凝土压酥区不断扩大, 承载力不断下降, 柱脚附近有大片混凝土碎屑下落, 箍筋和纵向钢筋裸露外鼓, 纵筋最大应变增至3.303×10-3, 荷载下降到最大荷载的80%以下, 停止加载, 试件XJZ失效, 其最终破坏形态如图 7(a)所示。

|
图 7 试件破坏形态 Fig. 7 Failure modes of specimens |
试件RECJZ1在位移为20 mm(加载力为247 kN) 之前, 未见明显裂缝出现, 整个试件基本仍处于弹性状态。加载侧移达28 mm(加载力为265 kN)时, 试件RECJZ1非加载侧连接钢板经过循环拉、压发生轻微压曲变形, 并出现“咔咔”声音, 连接节点附近无外包钢板的预制柱外皮也开始脱落。随着加载位移不断增加, 加载方向受压连接钢板与接缝相对应位置的鼓曲变形加大。当试件RECJZ1在侧移达-55 mm(加载力为251 kN)时, 加载方向的耗能连接钢板应变达5.408×10-3。加载位移至68 mm时, 试件达到极限承载力313 kN。当侧移达87 mm时(加载力为253 kN), 试件的最大承载力下降至峰值荷载的85%, 停止加载, 最终破坏形态见图 7(b)。
试件RECJZ2在侧移达7 mm前基本保持弹性状态, 未见明显损伤。加载位移至25 mm时, 试件达到极限承载力335 kN。加载侧移达40 m时(荷载为319 kN), 试件RECJZ2非加载侧连接钢板经过循环拉、压发生轻微压曲变形, 并出现“咔咔”的声音, 连接节点附近加载侧无外包钢板的预制柱混凝土外表皮也开始脱落。随着加载位移不断增加, 加载方向受压连接钢板与接缝相对应位置的鼓曲变形加大。当水平位移达70 mm(加载力为310 kN)时, 加载方向的连接耗能钢板应变达4.792×10-3, 此时受压侧连接钢板最大鼓曲达25 mm, 最终破坏形态如图 7(c)所示。与试件RECJZ2相比, 试件RECJZ1的连接钢板变形较小, 钢板鼓曲量明显小于前者, 原因在于短榫头连接部位在加载中更容易产生滑移, 约束作用小于长榫头, 钢板的变形没有得到充分发挥。
为了进一步评估RECJ节点修复后的抗震性能, 将试件RECJZ2复位, 更换已经损伤破坏的连接钢板, 完成试件修复。修复后的试件编号为RECJZ2-C, 再次进行拟静力试验至其破坏。试件RECJZ2-C整体加载循环响应与原试件类似, 且左、右两侧钢板的变形幅度与原试件几乎一致, 直至侧移达110 mm受压侧钢板断裂。此时, 由于其他3块连接钢板仍在发挥作用, 节点的承载力并未快速降低, 修复后试件RECJZ2-C的连接螺栓无明显变化, 混凝土除出现保护层脱落外也未见明显损伤。试件RECJZ2-C的变形和破坏情况详见图 7(d)。
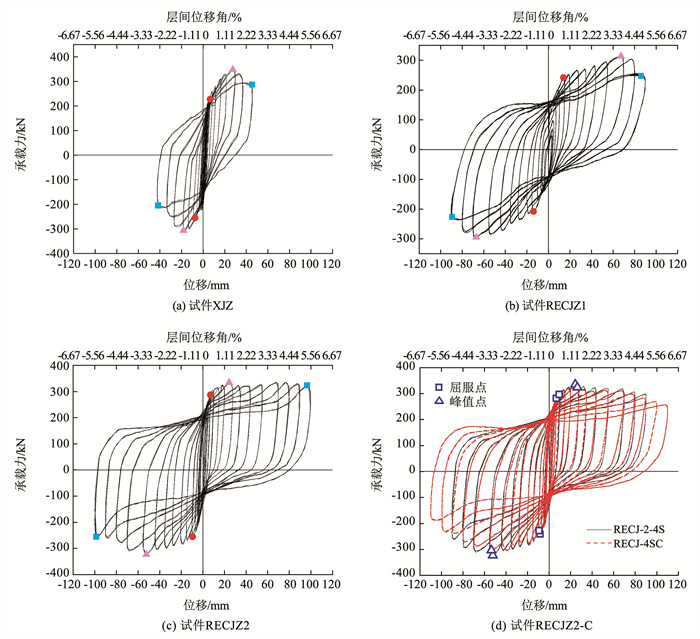
3.2 滞回性能4个试件的荷载-水平位移滞回曲线见图 8, 横坐标Δ表示加载端水平位移, 纵坐标P表示加载端水平力。由图 8可知:
|
图 8 试件滞回曲线 Fig. 8 Hysteresis curve of specimens |
1) 与试件XJZ的滞回曲线相比, 试件RECJZ1和RECJZ2的滞回曲线面积较大, 表现出良好的耗能性能;而且后者卸载至零后反向加载至残余变形为零时所需要的力比前者小。这是因为试件RECJZ1和RECJZ2的损伤主要集中在连接节点处, 依靠连接钢板及榫卯受力和变形而耗能, 而试件XJZ主要依靠柱下端塑性铰受力和变形而耗能。
2) 与试件XJZ的滞回曲线相比, 试件RECJZ1和RECJZ2在达到屈服位移后, 随位移幅值的增加荷载衰减速度缓慢, 有较长的强化阶段, 而且试件RECJZ2的荷载衰减速度比试件RECJZ1缓慢。这说明在试件RECJZ1和RECJZ2中, 主要依靠连接节点处的连接钢板和榫卯受力;试件RECJZ2的榫头长度比试件RECJZ1长, 故荷载衰减速度较缓。表明采用RECJ节点的试件具有良好的变形能力。
3) 试件RECJZ2-C加载面连接钢板局部出现断裂后, 由剩下的三面(正、反面和非加载面)连接钢板及榫卯共同承载, 其滞回曲线仍保持饱满, 且承载力并没有迅速衰减, 这说明RECJ节点在破坏时也能保持足够的承载力和刚度, 有利于防止结构的倒塌。
综上, 采用新型RECJ节点的装配柱具有明显优于试件XJZ的抗震性能, 适当加大连接部位榫头长度的新型RECJ节点的装配柱有利于提高其截面承载力、变形能力和耗能性能。
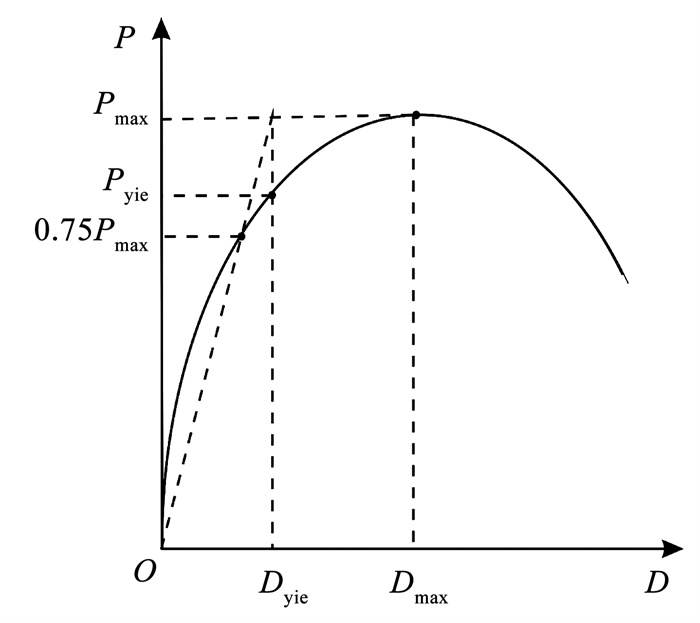
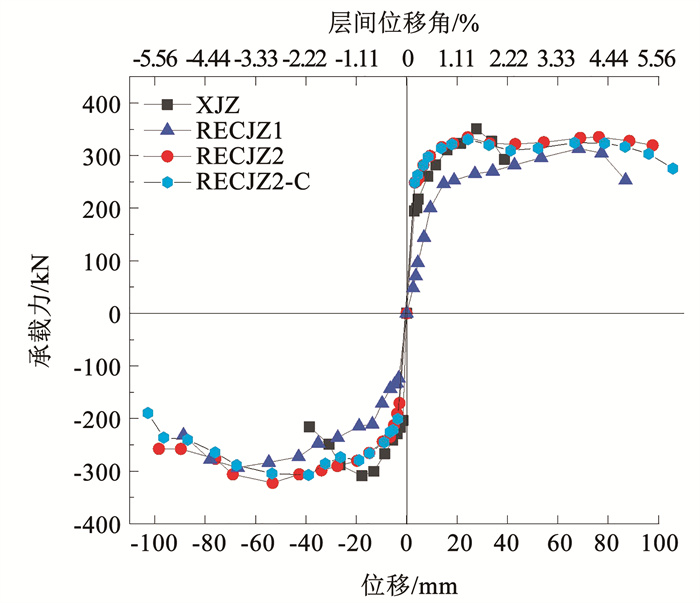
3.3 骨架曲线骨架曲线是每个加载循环中试件达到其最大水平力的轨迹, 涉及试件承载力和变形的各个阶段和特征, 如屈服、极限和破坏荷载及相应的位移等。如图 9所示, 屈服荷载通过塑性刚度法计算得到, 屈服位移则为屈服荷载相应的横坐标值;极限荷载取荷载-位移骨架曲线上最大荷载点对应的荷载;破坏荷载取85%极限荷载。图 10为3个试件的荷载-位移骨架曲线, 由这些曲线计算得到各试件的主要特征点参数, 见表 3(表中, Pyie、Pmax、Pult分别为屈服、极限和破坏荷载;Dyie、Dmax、Dult分别为屈服、极限和破坏荷载对应的位移)。分析图 10和表 3可知:
|
图 9 屈服荷载的计算 Fig. 9 Calculation of yield load |
|
图 10 骨架曲线 Fig. 10 Skeleton curves of specimens |
| 表 3 骨架曲线主要特征点试验结果 Tab. 3 Test results of main characteristic points of the skeleton curve |
1) 就各试件在达到屈服荷载之前的截面刚度而言, 与试件XJZ相比, 试件RECJZ2与试件XJZ的截面刚度基本相当, 而试件RECJZ1略低于试件XJZ。这表明就本试验而言, 当榫卯长度达到200 mm时, 装配式柱与现浇柱具有基本相等的截面刚度。
2) 试件RECJZ2正、反方向加载极限荷载平均值为332.2 kN, 试件XJZ的极限荷载平均值为330.6 kN, 二者非常接近。这表明就本试验而言, 当榫卯长度达到200 mm时, 装配式柱与现浇柱具有基本相等的极限水平承载力。
3) 试件RECJZ1和试件RECJZ2正、反方向加载极限位移平均值分别为87.81、82.95 mm, 而试件XJZ的极限位移平均值为38.7 mm, 试件RECJZ1和试件RECJZ2分别是试件XJZ的2.27倍和2.14倍。这表明新型装配式柱比普通现浇柱具有更好的变形性能。
4) 修复试件RECJZ2-C较原试件RECJZ2的屈服荷载下降了1.4%, 水平承载力下降3%, 二者的初始刚度几乎相同。这表明试件RECJ-2-4S在连接钢板失效后, 试件的非更换部分损伤较小, 试件损伤集中在可更换钢板上。
综上, 采用新型RECJ节点的装配柱具有较高的水平承载力和变形能力, 适当加大连接部位榫头长度, 可使这种装配式柱达到具有与现浇柱等同的初始刚度和水平承载力, 在大震下RECJ试件更换损伤的连接件后仍能恢复95%以上的抗震性能。
3.4 刚度退化试件在低周反复荷载作用下的刚度退化特性, 可采用实测割线刚度Ki表示, 即
| $ K_i=\frac{\left|+F_i\right|+\left|-F_i\right|}{\left|+\Delta_i\right|+\left|-\Delta_i\right|} $ | (1) |
式中:+Fi和-Fi分别为正、反向加载时, 第i次循环加载的荷载最大值;+Δi和-Δi分别为与其荷载对应的位移值。
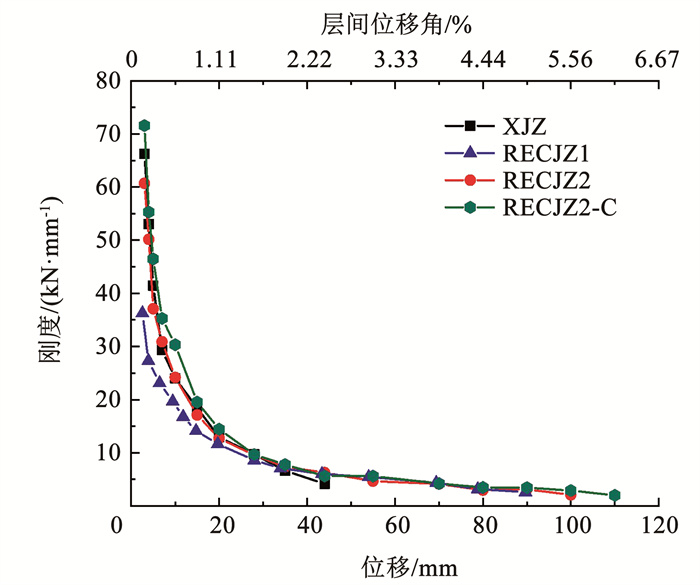
试件割线刚度退化曲线如图 11所示。可以看出, 试件RECJZ2与试件XJZ的初始刚度接近, 且退化规律亦基本相同;试件RECJZ1的初始刚度比试件XJZ小, 且退化速度较快;在试件顶点位移达到33 mm(1/50)时, 试件RECJZ1的割线刚度比试件XJZ小35%, 而试件RECJZ2的割线刚度比试件XJZ大10.8%。修复试件RECJZ2-C的割线刚度与原试件RECJZ2几乎相等。因此, 加大榫头长度可以有效地提高试件的整体割线刚度, 降低构件割线刚度退化程度。
|
图 11 刚度退化曲线 Fig. 11 Stiffness degradation curves of specimens |
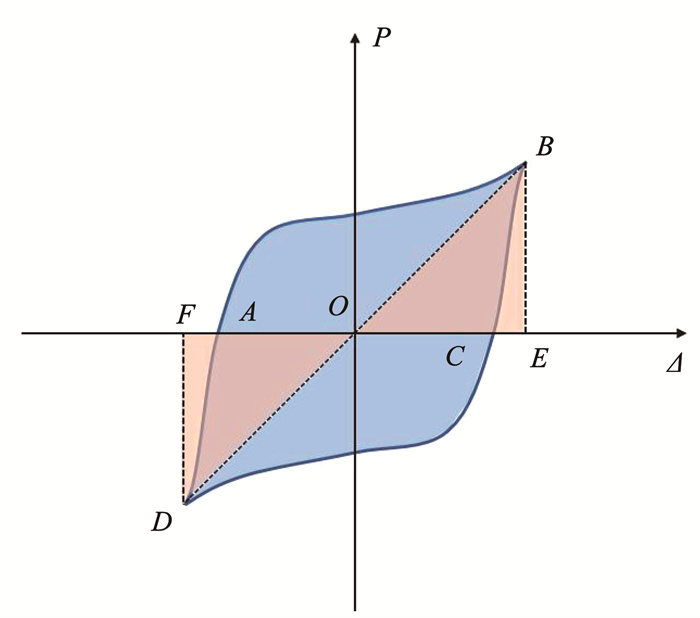
试件在一次循环加载过程中, 由于非弹性变形形成的“耗失能量”(通常简称为耗能)一般以荷载-变形滞回曲线所包围的面积(图 12)表示, 并采用能量耗散系数E来评价结构的耗能能力:
| $ E=\frac{S_{\overparen{A B C}+\overparen{C D A}}}{S_{\triangle O B E+\triangle O D F}} $ | (2) |
|
图 12 能量耗散系数的计算 Fig. 12 Calculation of energy dissipation coefficient |
式中:
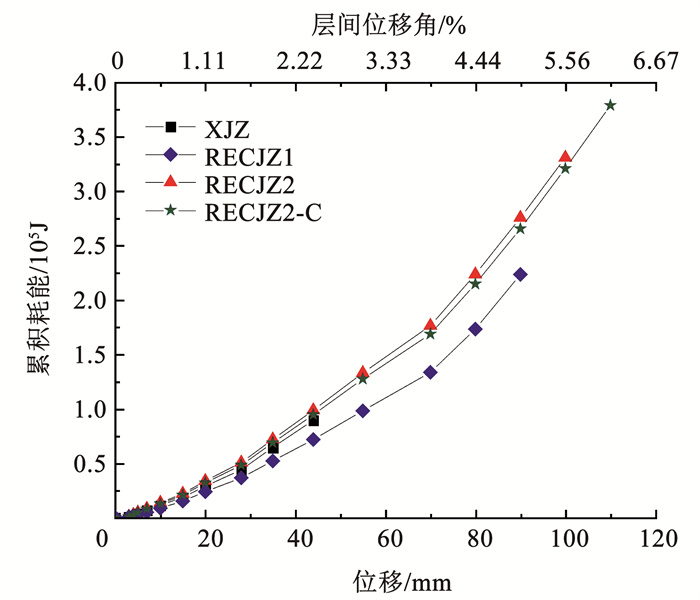
试件各阶段能量耗散系数如图 13所示。可以看出:
|
图 13 累积耗能 Fig. 13 Accumulate energy dissipation |
1) 达到各自极限荷载点时, 试件RECJZ1和试件RECJZ2的累积耗能约为试件XJZ的3.09倍和1.16倍;试件RECJZ2的累积耗能约为RECJZ1的2.66倍。
2) 达到各自破坏荷载点时, 试件RECJZ1和RECJZ2的累积耗能约为试件XJZ的3.39倍和5.09倍;试件RECJZ2的累积耗能约为RECJZ1的1.5倍。
3) 在水平位移达到90 mm时, 试件RECJZ2-C的累积耗能为原试件RECJZ2的0.94倍, 为RECJ-0-0的约2.8倍。
上述分析表明, 新型连接节点柱RECJZ试件比普通RC柱试件XJZ有更好的耗能能力。这是因为RECJZ试件主要依靠连接钢板耗能, 而试件XJZ主要依靠柱下端塑性铰耗能, 故前者比后者耗能能力强。
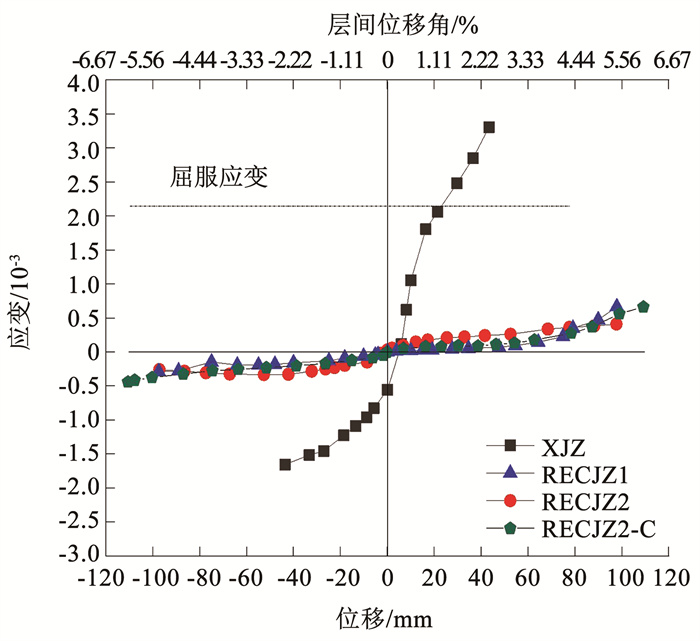
3.6 主要应变量测结果图 14为柱纵向受力钢筋应变与位移的关系曲线。可以看出, 实测纵筋屈服应变为2.113×10-3。由图 14及实测柱内纵向钢筋应变数据可知, 试件XJZ内纵筋最大应变为3.303×10-3, 超出钢筋屈服应变56%;而试件RECJZ2和试件RECJZ1由于连接部位以下柱身外包钢板及柱脚的加强作用, 纵筋应变普遍低于1.000×10-3, 其最大应变分别仅为纵筋屈服应变的19.4% 和31.6%;试件RECJZ1内纵筋最大应变比试件RECJZ2的高62.7%。这是由于RECJ柱中的外包钢板锚固在基础梁内, 减小了柱内纵筋的应力及应变;适当增长榫头长度, 可提高柱截面的整体性, 充分发挥连接钢板和榫头的承载作用。
|
图 14 柱钢筋位移-应变曲线 Fig. 14 Displacement-strain curve of reinforcements in column |
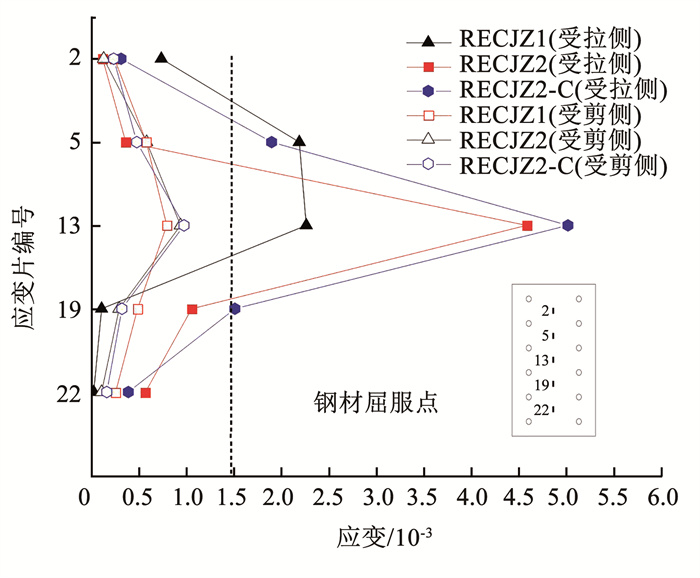
图 15为各试件连接钢板处各测点的应变值, 连接钢板的实测屈服应变为1.453×10-3(表 2)。图 15为当加载位移达33 mm(侧移角为2%)时, 试件加载平面内的两块连接钢板应变沿接缝位置不同的变化情况。可以看出, 连接接缝处钢板应变最大, 距接缝越远处的应变越来越小, 表明RECJ试件能有效地控制试件损伤在耗能板的连接部位, 也验证了螺栓连接的可靠性。此外, 试件RECJZ2接缝处最大应变比试件RECJZ1最大高102.5%, 说明增加榫头长度可以更加有效地将试件的损伤集中在更换元件上, 避免预制构件发生较大损伤或破坏, 有利于实现震后可修复的目的。
|
图 15 耗能钢板应变曲线 Fig. 15 Strain curves of energy-consuming in steel plate |
为便于计算RECJ应满足以下假设:
1) 装配节点处的钢板、混凝土榫头及凹槽均外包钢管, 变形较小, 计算时均可将其简化为刚体计算。
2) 凹槽内的橡胶层受到挤压时会对榫头有一定的作用力, 数值比较小, 可简化为线弹性材料。
3) 装配柱的变形仅考虑节点转角引起的位移和钢筋混凝土上柱自身转角产生的变形。
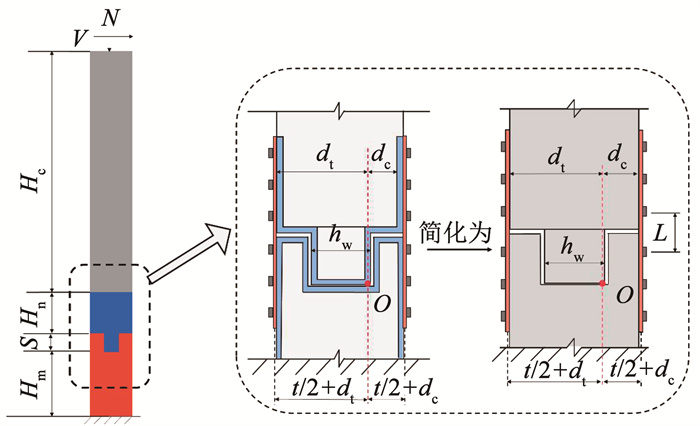
4) 假定上柱绕榫头底部端点O转动, 点O在榫头底, 如图 16所示。
|
图 16 装配柱节点示意 Fig. 16 Schematic diagram of precast column joint |
装配节点绕点O转动抗弯所需的承载力主要由4部分提供, 当水平加载力V的加载方向向右时, 4部分分别为:左侧耗能钢板受拉及右侧钢板受压引起的抵抗力Mb、前后两侧耗能钢板受弯引起的抵抗力Mh、榫头右侧受凹槽壁挤压引起的抵抗力Ms和加载的轴压力引起的绕点O的抵抗力MN。
在整个试验加载过程中, 装配节点的受弯承载过程主要可简化为3个阶段, 首先在受弯前期表现为前后左右4块耗能钢板的弹性阶段内承载和榫头与凹槽内壁的线形挤压承载, 这一阶段结束时为屈服状态;其次是耗能钢板到达屈服后的强化阶段内承载和榫头与凹槽内壁的双折线挤压承载, 这一阶段结束时为峰值状态;最后是耗能钢板的强度退化和二阶弯矩效应引起的承载下降段。
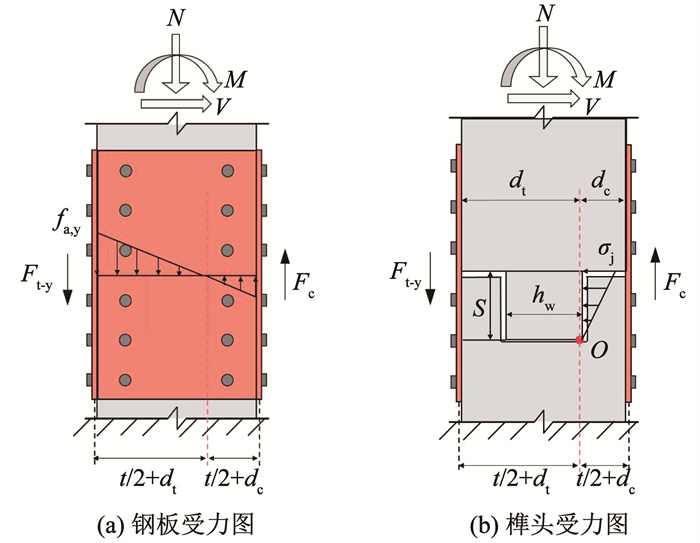
4.2 屈服状态RECJD的屈服阶段受力如图 17所示。
|
图 17 屈服状态下节点受力示意 Fig. 17 Schematic diagram of joint stress under yield state |
节点抗弯在到达屈服状态时, 其特征主要表现为:左侧耗能钢板受拉到达屈服点、右侧耗能钢板受压到达临界失稳状态、榫头右侧压应力由于橡胶挤压呈三角形分布。因此, 节点在屈服状态下的受弯承载力Mj-y按下式计算:
| $ M_{\mathrm{j}-\mathrm{y}}=M_{\mathrm{N}-\mathrm{y}}+M_{\mathrm{h}-\mathrm{y}}+M_{\mathrm{s}-\mathrm{y}} $ | (3) |
轴压力N产生绕点(4)O的抵抗弯矩MN-y, 在屈服状态下节点转动较小, 由于凹槽底部的橡胶, 可近似认为榫头底部的压应力为三角形分布, 因此, MN-y可按下式计算:
| $ M_{\mathrm{N}-\mathrm{y}}=N \frac{h_{\mathrm{w}}}{3} $ | (4) |
式中hw为榫头的截面高度。
左侧耗能钢板受拉屈服和右侧耗能钢板受压屈曲引起的绕O点的抵抗弯矩Mb-y按下式计算:
| $ M_{\mathrm{b}-\mathrm{y}}=F_{\mathrm{t}-\mathrm{y}}\left(d_{\mathrm{t}}+\frac{t}{2}\right)+F_{\mathrm{c}}\left(d_{\mathrm{c}}+\frac{t}{2}\right) $ | (5) |
式中:Ft-y为左侧耗能钢板因受拉到达屈服时的拉力;dt为点O到左侧耗能钢板内表面的距离, 为290 mm。拉力Ft-y、临界失稳力Fc分别按式(6)、(7)计算:
| $ F_{\mathrm{t}-\mathrm{y}}=f_{\mathrm{ay}} b_{\mathrm{lt}} $ | (6) |
| $ F_\text{c}=\sigma_\text{c} b t $ | (7) |
式中:fay为耗能钢板材料的屈服强度;blt为左侧耗能钢板的截面净宽(即钢板宽度减去螺栓孔直径的宽度);t为钢板厚度;b为右侧耗能钢板宽度;σc为右侧耗能钢板截面均匀受压产生的临界失稳应力。
前后两侧的两块耗能钢板承受压和拉联合作用, 其应力分布近似为线性分布, 见图 17(a), 其中, 最大拉应力为fay, 中性轴竖直经过O点, 因此, 前后两侧耗能钢板绕点O的抵抗弯矩Mh-y可按下式计算:
| $ M_{\mathrm{h}-\mathrm{y}}=2 f_{\mathrm{ay}} t \frac{d_{\mathrm{t}}^3+d_{\mathrm{c}}^3}{3 d_{\mathrm{t}}} $ | (8) |
由于节点的转动, 榫头右侧会受到挤压橡胶产生的侧向分布压应力作用, 其分布近似为三角形, 最大压应力为σj, 因此, 榫头侧向分布压应力引起的绕点O的弯矩Ms-y可按下式计算:
| $ M_{\mathrm{s}-\mathrm{y}}=\frac{\sigma_{\mathrm{j}} b_{\mathrm{w}} s^2}{3} $ | (9) |
式中:s为榫头的长度;bw为榫头的截面宽度。
综上, 装配节点的屈服弯矩计算如下:
| $ \begin{aligned} M_{\mathrm{j}-\mathrm{y}}= & N \frac{h_{\mathrm{w}}}{3}+f_{\mathrm{ay}} b_{\mathrm{t}} t\left(d_{\mathrm{t}}+\frac{t}{2}\right)+\sigma_{\mathrm{c}} b t\left(d_{\mathrm{c}}+\frac{t}{2}\right)+ \\ & 2 f_{\mathrm{a}, \mathrm{y}} t \frac{d_{\mathrm{t}}^3+d_{\mathrm{c}}^3}{3 d_{\mathrm{t}}}+\frac{\sigma_{\mathrm{j}} b_{\mathrm{w}} s^2}{3} \end{aligned} $ | (10) |
节点在到达屈服状态时的转角变形为θj-p, 主要表现为左侧耗能钢板受拉变形引起的绕点O的转动, 可按下式近似计算:
| $ \theta_{\mathrm{j}-\mathrm{y}}=\frac{\varepsilon_{\mathrm{a}, \mathrm{y}} d}{\frac{t}{2}+d_{\mathrm{t}}} $ | (11) |
式中:d为中间两行相邻螺栓的间距, εa, y为耗能钢板材料的屈服应变, 其取值见表 2。
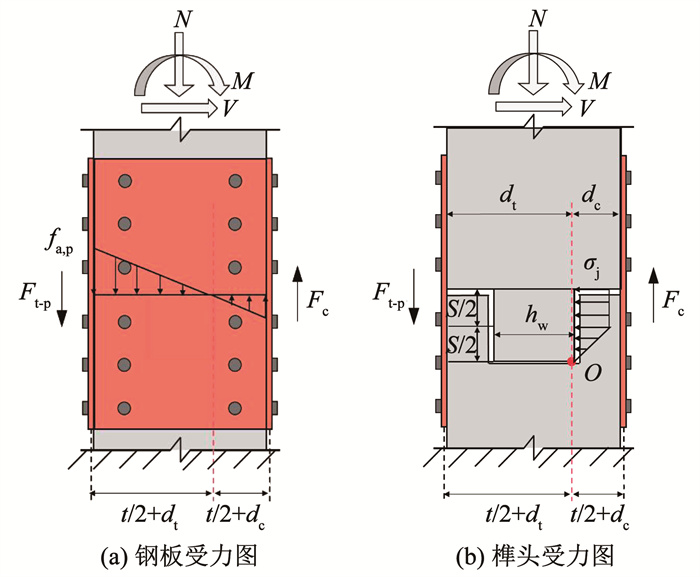
4.3 极限状态峰值状态下装配节点处的受力计算简图如图 18所示。
|
图 18 屈服状态下节点受力示意 Fig. 18 Schematic diagram of joint stress under peak state |
强化承载阶段的最终时刻为峰值承载状态, 近似认为节点此时主要特征为:左侧耗能钢板受拉到达强化后的极限强度fa, u, 竖向轴压力因水平位移产生较大的附加弯矩, 且榫头侧向压应力分布近似改变为双折线。假定右侧耗能钢板仍为受压屈曲状态, 此状态下的节点受力计算简图见图 18。则节点峰值受弯承载力Mj-p的计算如下:
| $ M_{\mathrm{j}-\mathrm{p}}=M_{\mathrm{N}-\mathrm{p}}+M_{\mathrm{h}-\mathrm{p}}+M_{\mathrm{b}-\mathrm{p}}+M_{\mathrm{s}-\mathrm{p}} $ | (12) |
在峰值状态下, 榫头转动角度较大, 考虑到轴压力引起的二阶弯矩效应, 轴压力产生的绕点O的抵抗弯矩MN-p会减小, 因此, 轴压力引起的抵抗弯矩MN-p按下式近似计算:
| $ M_{\mathrm{N}-\mathrm{p}}=N \frac{h_{\mathrm{w}}}{6} $ | (13) |
左侧耗能钢板受拉和右侧耗能钢板受压屈曲绕点O转动引起的抵抗弯矩Mb-p按下式计算:
| $ M_{\mathrm{b}-\mathrm{p}}=F_{\mathrm{t}-\mathrm{p}}\left(d_{\mathrm{t}}+\frac{t}{2}\right)+F_{\mathrm{c}}\left(d_{\mathrm{c}}+\frac{t}{2}\right) $ | (14) |
| $ F_{\mathrm{t}-\mathrm{p}}=f_{\mathrm{a}, \mathrm{u}} b_1 t $ | (15) |
式中:Ft-p为左侧耗能钢板截面受拉产生的拉力, fa, u为耗能钢板材料的极限强度。
前后两侧耗能钢板受到线性分布的拉压应力作用, 其最大拉应力到达钢板材料极限强度fa, u, 且其中性轴竖直过点O, 如图 18(b)所示。因此, 两块钢板因受弯而引起的绕点O的抵抗弯矩Mh-p按下式计算:
| $ M_{\mathrm{h}-\mathrm{p}}=2 f_{\mathrm{a}, \mathrm{u}} t \frac{d_{\mathrm{t}}^3+d_{\mathrm{c}}^3}{3 d_{\mathrm{t}}} $ | (16) |
榫头右侧受到的橡胶挤压应力近似认为是沿榫头长度呈双折线形分布, 如图 18(b)所示, 因此, 引起的榫头绕点O的抵抗弯矩Ms-p计算如下:
| $ M_{\mathrm{s}-\mathrm{p}}=\frac{11 \sigma_{\mathrm{j}} b_{\mathrm{w}} s^2}{24} $ | (17) |
故峰值状态下节点弯矩承载力的计算如下:
| $ \begin{aligned} M_{\mathrm{j}-\mathrm{p}}= & N \frac{h_{\mathrm{w}}}{6}+f_{\mathrm{a}, \mathrm{u}} b_{\mathrm{l}} t\left(d_{\mathrm{t}}+\frac{t}{2}\right)+\sigma_{\mathrm{c}} b t\left(d_{\mathrm{c}}+\frac{t}{2}\right)+ \\ & 2 f_{\mathrm{a}, \mathrm{u}} t \frac{d_{\mathrm{t}}^3+d_{\mathrm{c}}^3}{3 d_{\mathrm{t}}}+\frac{11 \sigma_{\mathrm{j}} b_{\mathrm{w}} s^2}{24} \end{aligned} $ | (18) |
节点到达峰值承载状态时, 装配节点的转角变形θj-p仍以左侧耗能钢板受拉引起的变形为主, 此时耗能钢板受拉到达峰值应变, 转动计算如下:
| $ \theta_{\mathrm{j}-\mathrm{p}}=\frac{\varepsilon_{\mathrm{a}, \mathrm{p}} d}{\frac{t}{2}+d_{\mathrm{t}}} $ | (19) |
式中:εa, p为耗能钢板材料峰值强度对应的应变, 其大小见表 2; d为中间两行相邻螺栓间距。
采用薄板小挠度理论[24]得到σc的表达式:
| $ \sigma_c=k \frac{\pi^2 E t^2}{12\left(1-v^2\right) b^2} $ | (20) |
已知受压侧钢板的a=100 mm, b=400 mm, t=4 mm, E=181.004 GPa, υ=0.3, 求得K=9.107 2, σc=148.98 N/mm2。
4.4 骨架曲线模型由试验可知, 装配柱破坏均以节点部位破坏为主, 因此, 装配柱的水平承载力即可由节点受弯承载力确定。装配柱在屈服状态和峰值状态下的水平承载力Vy、Vp如下:
| $ V_y=\frac{M_{\mathrm{j}-\mathrm{y}}}{H_1} $ | (21) |
| $ V_{\mathrm{p}}=\frac{M_{\mathrm{j}-\mathrm{p}}}{H_1} $ | (22) |
各特征点的理论荷载值与试验荷载值对比见表 4。可以看出, 试件RECJZ-1、RECJZ-2的受弯承载力计算公式还是比较符合试验结果的, 试件RECJZ-1的理论屈服荷载与试验的屈服荷载均值相差20%, 主要是由螺栓杆的滑移和榫头在凹槽内的少量侧移引起的。
| 表 4 特征点荷载对比 Tab. 4 Comparison of characteristic point loads |
混凝土上柱为一弹性悬臂梁, 且在屈服状态时就已经到达其弹性极限转角θc-y, 随后在峰值和极限状态下都保持不变。装配柱特征点下对应的水平位移可按下式计算:
| $ \Delta_\text{y}=H_1 \theta_\text{j-y}+H_1 \theta_\text{c-y} $ | (23) |
| $ \Delta_{\mathrm{p}}=H_1 \theta_{\mathrm{j}-\mathrm{p}}+H_1 \theta_{\mathrm{c}-\mathrm{y}} $ | (24) |
式中:Δy、Δp分别为屈服状态、峰值状态下的加载点水平位移;θj-y、θj-p分别为对应状态下的节点转角变形。
关于混凝土上柱的转角变形弹性极限值θc-y的计算, 只需对混凝土上柱进行积分即可, 即
| $ \theta_\text{c-y}=\int_0^{H_{\mathrm{c}}} \frac{M_{\mathrm{c}-\mathrm{y}}}{H_{\mathrm{c}} K_{\mathrm{c}-\mathrm{v}}^{\prime}} x \mathrm{~d} x=\frac{M_{\mathrm{c}-\mathrm{y}} H_{\mathrm{c}}}{2 K_{\mathrm{c}-\mathrm{v}}^{\prime}}=\frac{H_{\mathrm{c}} \theta_{\mathrm{c}-\mathrm{y}}^{\prime}}{2} $ | (25) |
| $ K_\text{c-y}^{\prime}=\frac{M_\text{c}}{\theta_\text{c-y}^{\prime}} $ | (26) |
| $ \theta_{\mathrm{c}-\mathrm{y}}^{\prime}=\frac{\varepsilon_{\mathrm{s}, \mathrm{y}}+\varepsilon_{\mathrm{cu}}}{h} $ | (27) |
式中:Hc为混凝土上柱高度;K′ c-y为混凝土截面转动刚度, 计算见式(26);Mc-y为受拉钢筋屈服时的混凝土截面最大弯矩;θ′ c-y为受拉纵筋屈服时的混凝土截面转角, 计算见式(27);εs, y为钢筋屈服应变, 取0.002 113;εcu为混凝土极限应变, 取0.003 3。
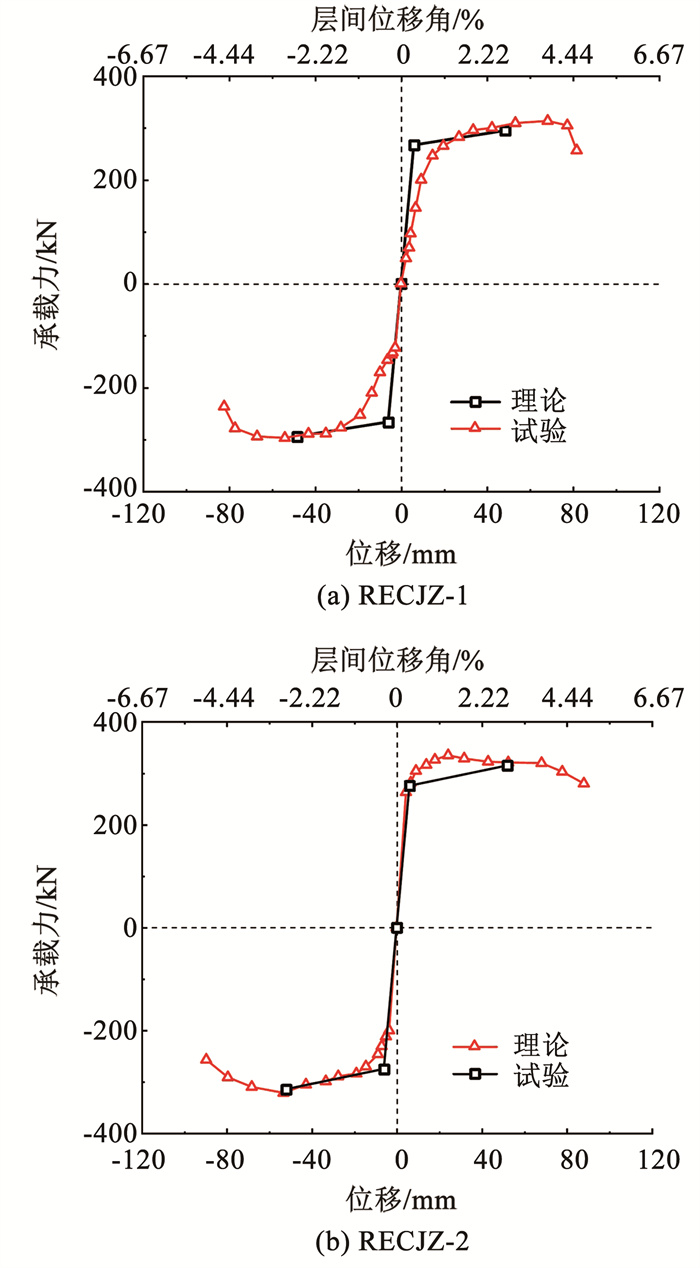
图 19为得到的骨架曲线模型。
|
图 19 骨架曲线模型 Fig. 19 Skeleton curve model diagram |
由图 19可以看出, 骨架曲线模型和试验得到的骨架曲线整体趋势保持一致, 且理论计算的节点屈服荷载、峰值荷载与试验结果较为接近。可知装配柱的理论承载力公式与试验结果较为吻合。
5 结论提出了一种“榫卯+连接钢板”的新型柱间连接节点, 通过对3个试件的拟静力加载试验及结果分析, 得到如下主要结论:
1) 在柱截面尺寸、剪跨比、纵筋配筋率、混凝土强度均相同的情况下, 现浇柱试件XJZ为压弯破坏, 破坏集中在柱下端塑性铰区, 震后难以修复。而新型连接节点柱RECJZ试件的破坏集中在连接钢板部位, 柱内纵筋应变远小于其屈服应变, 试件破坏时纵筋尚处于弹性阶段, 震后只需更换外包连接钢板, 即可恢复其承载功能。
2) 在榫卯长度、连接钢板厚度、连接螺栓间距均合适时, 新型连接节点柱RECJZ试件的初始刚度和水平极限承载力均等同于或略高于现浇柱试件XJZ。
3) 新型连接节点柱RECJZ试件的极限变形是现浇试件XJZ的2倍多, 前者的耗能系数约是后者的5倍, 说明新型连接节点柱RECJZ试件有良好的变形和耗能能力。
4) 推导了RECJ柱的承载力计算公式, 并给出了三折线抗侧骨架曲线模型, 与试验骨架曲线进行对比验证了公式和模型的可行性。
5) 榫卯长度、连接钢板厚度、连接螺栓间距是影响这种柱刚度和承载力的关键参数, 其合理取值范围尚需进一步研究。
| [1] |
清华大学土木工程结构专家组, 西南交通大学土木工程结构专家组, 北京交通大学土木工程结构专家组, 等. 汶川地震建筑震害分析[J]. 建筑结构学报, 2008, 29(4): 1. Civil Engineering Structure Expert Group of Tsinghua University, Civil Engineering Structure Expert Group of Southwest Jiaotong University, Civil Engineering Structure Expert Group of Beijing Jiaotong University, et al. Analysis of building damage in wenchuan earthquake[J]. Journal of Building Structures, 2008, 29(4): 1. DOI:10.14006/j.jzjgxb.2008.04.001 |
| [2] |
中华人民共和国住房和城乡建设部. 建筑抗震设计规范: GB 50011—2010[S]. 北京: 中国建筑工业出版社, 2016 Ministry of Housing and Urban Rural Development of the People's Republic of China. Code for seismic design of buildings: GB 50011—2010[S]. Beijing: China Construction Industry Press, 2016 |
| [3] |
周绪红, 刘界鹏. 钢管约束混凝土柱的性能与设计[M]. 北京: 科学出版社, 2010. ZHOU Xuhong, LIU Jiepeng. Performance and design of steel tube confined concrete column[M]. Beijing: Science Press, 2010. |
| [4] |
姜子钦, 杨晓峰, 张爱林, 等. 可恢复功能装配式中柱节点耗能装置试验研究[J]. 建筑结构学报, 2020, 41(1): 15. JIANG Ziqin, YANG Xiaofeng, ZHANG Ailin, et al. Experimental study on energy dissipation device of assembled central column node with recoverable function[J]. Journal of Building Structures, 2020, 41(1): 15. DOI:10.14006/j.jzjgxb.2018.0598 |
| [5] |
WU Chenglong, LIU Jiming, TAN Wenya, et al. Seismic behavior of composite interior joints of prefabricated H-shaped steel reinforced concrete column-steel beam[J]. Structures, 2020, 23: 558. DOI:10.1016/j.istruc.2019.11.008 |
| [6] |
LU Zhiwei, HUANG Jun, DAI Shaobin, et al. Experimental study on a precast beam-column joint with double grouted splice sleeves[J]. Engineering Structures, 2019, 199: 109589. DOI:10.1016/j.engstruct.2019.109589 |
| [7] |
吴刚, 冯德成. 装配式混凝土框架节点基本性能研究进展[J]. 建筑结构学报, 2018, 39(2): 1. WU Gang, FENG Decheng. Research progress on basic performance of prefabricated concrete frame joints[J]. Journal of Building Structures, 2018, 39(2): 1. DOI:10.14006/j.jzjgxb.2018.02.001 |
| [8] |
李青宁, 郑先超, 颜志勇, 等. 高强螺旋箍筋约束混凝土柱连接抗震性能试验研究与理论分析[J]. 建筑结构学报, 2013, 34(8): 90. LI Qingning, ZHENG Xianchao, YAN Zhiyong, et al. Experimental study and theoretical analysis of seismic performance of concrete column connections confined by high-strength spiral stirrups[J]. Journal of Building Structures, 2013, 34(8): 90. DOI:10.14006/j.jzjgxb.2013.08.011 |
| [9] |
郑先超. 新型装配式混合结构抗震体系试验及理论分析[D]. 西安: 西安建筑科技大学, 2013 ZHENG Xianchao. Experimental and theoretical analysis of seismic system of new prefabricated hybrid structure[D]. Xi'an: Xi'an University of Architecture and Technology, 2013 |
| [10] |
郑先超, 阎利, 李青宁, 等. 局部外包钢管栓杆式高强箍筋约束混凝土柱与柱连接试验研究与有限元分析[J]. 结构工程师, 2015, 31(4): 182. ZHENG Xianchao, YAN Li, LI Qingning, et al. Experimental study and finite element analysis of connection between concrete column and column confined by locally-clad steel pipe bolt-type high-strength stirrups[J]. Structural Engineer, 2015, 31(4): 182. DOI:10.15935/j.cnki.jggcs.2015.04.026 |
| [11] |
张兴虎, 应一辉, 潘树宾, 等. 装配整体式浆锚插筋及钢板箍连接柱试验研究[J]. 西安建筑科技大学学报(自然科学版), 2012, 44(3): 310. ZHANG Xinghu, YING Yihui, PAN Shubin, et al. Experimental study on assembly of integral grout anchor inserts and steel plate hoop connecting column[J]. Journal of Xi'an University of Architecture and Technology (Natural Science Edition), 2012, 44(3): 310. DOI:10.15986/j.1006-7930.2012.03.018 |
| [12] |
应一辉. 装配整体式浆锚插筋连接混凝土柱抗震性能试验研究[D]. 西安: 西安建筑科技大学, 2012 YING Yihui. Experimental study on the seismic performance of assembled monolithic grout-anchored and reinforced concrete columns[D]. Xi'an: Xi'an University of Architecture and Technology, 2012 |
| [13] |
张微敬, 王桂洁, 张晨骋, 等. 钢筋机械连接的装配式框架抗震性能试验研究与有限元分析[J]. 土木工程学报, 2019, 52(5): 47. ZHANG Weijing, WANG Guijie, ZHANG Chencheng, et al. Experimental study and finite element analysis of seismic performance of prefabricated frames with mechanical connections of steel bars[J]. China Civil Engineering Journal, 2019, 52(5): 47. DOI:10.15951/j.tmgcxb.2019.05.005 |
| [14] |
马哲昊, 张纪刚, 梁海志, 等. 人工消能塑性铰装配式钢筋混凝土框架结构抗震性能[J]. 哈尔滨工程大学学报, 2020, 41(4): 535. MA Zhehao, ZHANG Jigang, LIANG Haizhi, et al. Seismic performance of artificial energy dissipation plastic hinge assembly reinforced concrete frame structure[J]. Journal of Harbin Engineering University, 2020, 41(4): 535. DOI:10.11990/jheu.201812084 |
| [15] |
吕英婷, 郭子雄, 黄婷婷, 等. 装配式震损可更换组合柱抗震性能试验研究[J]. 土木工程学报, 2020, 53(4): 1. LV Yingting, GUO Zixiong, HUANG Tingting, et al. Experimental study on seismic performance of prefabricated seismic damaged replaceable composite columns[J]. China Civil Engineering Journal, 2020, 53(4): 1. DOI:10.15951/j.tmgcxb.2020.04.001 |
| [16] |
李春雨, 童超, 吴京, 等. 可更换耗能连接件的装配式混凝土框架结构抗震性能试验研究[J]. 建筑结构学报, 2022, 43(1): 69. LI Chunyu, TONG Chao, WU Jing, et al. Experimental study on seismic performance of prefabricated concrete frame structures with replaceable energy-consuming connections[J]. Journal of Building Structures, 2022, 43(1): 69. DOI:10.14006/j.jzjgxb.2020.0151 |
| [17] |
刘阳, 郭子雄, 贾磊鹏, 等. 震损可更换组合柱抗震性能试验研究[J]. 建筑结构学报, 2020, 41(7): 45. LIU Yang, GUO Zixiong, JIA Leipeng, et al. Experimental study on seismic performance of replaceable composite columns damaged by earthquake[J]. Journal of Building Structures, 2020, 41(7): 45. DOI:10.14006/j.jzjgxb.2018.0150 |
| [18] |
罗青儿, 张仟朋, 程文瀼, 等. 装配整体式钢筋混凝土框架柱榫式接头的试验研究[J]. 工业建筑, 2008(10): 48. LUO Qinger, ZHANG Qianpeng, CHENG Wenying, et al. Experimental study on the tenon joints of assembled monolithic reinforced concrete frame columns[J]. Industrial Construction, 2008(10): 48. DOI:10.13204/j.gyjz2008.10.014 |
| [19] |
汪梅, 梁书亭, 李刻铭, 等. 新型全装配式干式连接框架柱的试验研究[J]. 建筑技术, 2010, 41(1): 52. WANG Mei, LIANG Shuting, LI Keming, et al. Experimental research on a new type of fully assembled dry connection frame column[J]. Building Technology, 2010, 41(1): 52. DOI:10.3969/j.issn.1000-4726.2010.01.016 |
| [20] |
汪梅, 吴炯, 何孝春, 等. 钢筋混凝土全预制柱的受力分析[J]. 特种结构, 2011, 28(5): 9. WANG Mei, WU Jiong, HE Xiaochun, et al. Force analysis of reinforced concrete fully precast columns[J]. Special Structure, 2011, 28(5): 9. DOI:10.3969/j.issn.1001-3598.2011.05.003 |
| [21] |
中华人民共和国住房和城乡建设部. 混凝土物理力学性能试验方法标准: GB/T 50081—2019[S]. 北京: 中国建筑工业出版社, 2019 Ministry of Housing and Urban Rural Development of the People's Republic of China. Standard for test methods of physical and mechanical properties of concrete: GB/T 50081—2019[S]. Beijing: China Building Industry Press, 2019 |
| [22] |
国家市场管理总局. 金属材料拉伸试验第1部分: 室温试验方法: GB/T 228.1―2010[S]. 北京: 中国标准出版社, 2010 State Administration for Market Regulation. Tensile test of metallic materials part 1: room temperature test method: GB/T 228.1―2010[S]. Beijing: China Standard Press, 2010 |
| [23] |
ACI. Acceptance criteria for moment frames based on structural testing and commentary[S]. Farmington Hills: American Concrete Institute, 2005
|
| [24] |
TIMOSHENKO S P. Theory of elasticity[M]. Beijing: Science Press, 1970.
|
 2024, Vol. 56
2024, Vol. 56


