2. 大连理工大学 建设工程学部,辽宁 大连 116024
2. Faculty of Infrastructure Engineering, Dalian University of Technology, Dalian 116024, Liaoning, China
通常,大型公共建筑内区面积比重大,室内热源散热量大,其实时冷负荷对建筑运行能耗影响大。在冬季,大型公建不仅经常存在因内区过热而需要供冷的现象,而且存在因没有考虑内区热源散热而过度供热的问题,使得大型公建冬季室内热舒适性差、供暖能耗高。在夏季,大型公建内区室内热源的存在,不仅增加了建筑空调冷负荷,也增大了内区乃至整栋建筑空调运行调控的难度。若能准确获取内热源实时冷负荷大小和动态趋势,可以有效减小空调系统运行能耗,降低建筑碳排放。相对内热源对流热形成的瞬时冷负荷,辐射热形成的滞后冷负荷较难计算,这是因为辐射热在围护结构中经历复杂的蓄放热过程,导致滞后冷负荷具有时间延迟及幅度衰减特点,因此,如何科学地获取建筑内热源实时负荷大小和动态趋势,及利用数学方式描述辐射冷负荷时间滞后特性及幅度衰减规律等问题有必要进行深入研究。
为获取建筑内热源逐时冷负荷,《实用暖通空调设计手册》[1]和《暖通空调》[2]给出冷负荷系数,该系数可以描述内热源冷负荷的动态变化特性。虽然冷负荷系数在设计过程及工程项目中应用较广泛,但是仍然存在以下不足:1)只给出轻、中、重3种典型围护结构的冷负荷系数值,很难应用于实际工况下各类围护结构的计算过程;2)该方法只适用于内热源的理想工作工况,即24 h内只工作1次,对于工作频率高、工作时间不固定的内热源,该方法很难得出合理结果;3)冷负荷时间系数表示内热源总散热与冷负荷的逐时比例关系,其中包含对流热产生的瞬时冷负荷部分,所以,冷负荷时间系数无法准确描述围护结构对辐射热的蓄放热作用。Wei等[3]利用摄像机、记录仪等电子设备实时获取内热源散热情况。此外,实时电功率法[4]、调查问卷法[5-6]等也用于内热源实时冷负荷的获取过程。但是,上述方法将瞬时与滞后冷负荷合并计算,计算精度很难保证,而且无法描述滞后冷负荷的时间延迟性。内热源滞后冷负荷占建筑总体冷负荷的26.55%~45.00%[7-10],单独、准确地获取该数据具有重要意义。
为单独获取内热源辐射热所产生的滞后冷负荷,Spitler等[11]推荐使用比例指标值获取各类设备滞后冷负荷,例如,电脑类设备滞后冷负荷占比为0.2~0.8。但是,宽泛的比例范围令计算结果具有主观性,很难保证其精度。为降低主观性,提高计算精度,Hosni等[12]通过试验给出常见设备滞后冷负荷比例指标值。但是,在设备运行工况,滞后冷负荷与散热量之间呈现复杂的动态比例关系[13],简单地用固定指标值进行计算不仅精度低、无法体现滞后冷负荷的动态规律,而且很难描述围护结构蓄放热过程引起的时间滞后特性。
为描述室内热源滞后冷负荷动态变化规律及时间滞后特性,ASHRAE Handbook of Fundamentals[8]推荐使用辐射时间系数法(radiant time series method, RTS)计算电子类设备逐时冷负荷,并给出18种典型围护结构的辐射时间系数[14]。虽然该方法在全世界范围内广泛应用,但是计算过程十分繁琐,需要参考48个参数才能获取某一时刻的冷负荷数值,令计算过程更加复杂,不仅耗费大量时间,而且容易造成计算误差,实际工况下应用价值较低。
综上,针对室内热源滞后冷负荷动态特性实时监测计算问题,首先,基于围护结构蓄放热规律、热传递机制等建立滞后冷负荷监测模型,然后,基于辐射时间系数对模型进行参数辨识及降阶分析,最后,结合提出的内热源滞后冷负荷传递函数模型及辐射时间系数,定性定量分析得出围护结构蓄放热过程的影响因素。本研究为准确获取大型公共建筑室内热源实时负荷、提高空调系统节能调控水平、降低建筑运行能耗提供了理论基础方法。
1 内热源滞后热冷负荷传递函数模型的建立建筑室内热源主要由人员、设备和灯具组成,其辐射热在围护结构和室内固体内部会发生复杂的蓄放热过程(如图 1所示),导致内热源辐射热与冷负荷存在时间上的延迟和幅度上的衰减[15](如图 2所示),所以,辐射热引起的滞后冷负荷对于准确获取实时冷负荷至关重要。

|
图 1 围护结构及室内固体蓄放热过程 Fig. 1 Heat release and storage process of building envelope and indoor solids |
在实际工况下,内热源各表面发射率、角系数及温度等参数不一定相等,本文在计算辐射热时将各表面考虑进来。对于某一内热源,其辐射散热量计算方法[16]如下:
| $ \begin{aligned} \dot{Q}_{\mathrm{R}}= & \sum\limits_{j=1}^{n_{\mathrm{R}}} \sum\limits_{k=1}^{n_{\mathrm{e}}} \varepsilon_j \sigma_{\mathrm{b}} X_{\mathrm{c} j, \mathrm{ek}} A_{\mathrm{R} j}\left(T_{\mathrm{cj}}^4-T_{\mathrm{ek}}^4\right)+ \\ & \sum\limits_{j=1}^{n_{\mathrm{R}}} \sum\limits_{m=1}^{n_{\mathrm{g}}} \varepsilon_j \sigma_{\mathrm{b}} X_{\mathrm{c}j, \mathrm{~g} m} A_{\mathrm{R} j}\left(T_{\mathrm{cj}}^4-T_{\mathrm{g} m}^4\right) \end{aligned} $ | (1) |
式中:εj为内热源表面j的法向发射率;σb为黑体辐射常数,也称为斯蒂芬-玻尔兹曼常数,σb=5.67×10-8W/(m2·K4);Xcj, ek为内热源表面j与围护结构表面k的角系数;ARj为内热源表面j的辐射散热面积,m2;Tcj为内热源表面j的热力学温度,K;Tek为围护结构表面k的热力学温度,K;nR为内热源参与辐射散热的表面数量;ne,ng分别为围护结构和室内固体参与辐射散热的表面数量;Xcj, gm为内热源表面j与周围固体表面m的角系数;Tgm为周围固体表面m的热力学温度,K。
在散热过程中,内热源各表面的温度、传热系数等不一定相等,故分别对各表面自然对流散热量进行计算。不失一般性,考虑内热源中部分电子设备(如电脑)与周围环境的对流散热量包括自然对流与受迫对流两部分。对于某一内热源,其对流散热量计算方法[16]如下:
| $ \dot{Q}_{\mathrm{V}}=\sum\limits_{i=1}^{n_{\mathrm{V}}} h_{\mathrm{c} i} A_{\mathrm{V} i}\left(t_{\mathrm{c} i}-t_{\mathrm{a}}\right)+c_{\mathrm{a}} \rho_{\mathrm{a}} q_{\mathrm{f}}\left(t_{\mathrm{f}}-t_{\mathrm{a}}\right) $ | (2) |
式中:nV为内热源参与对流散热的表面数量;hci为内热源表面i的对流换热系数,W/(m2·℃);AVi为内热源表面i的对流散热面积,m2;tci为内热源表面i的温度,℃;ta为室内空气温度,℃;ca为空气的定压比热容,J/(kg·℃);ρa为空气密度,kg/m3;qf为内热源单位时间内受迫对流空气流量(如电脑散热风扇的风量),m3/s;tf为内热源受迫对流空气温度(如电脑散热风扇的排风温度),℃。
内热源辐射散热引起的冷负荷计算方法如下:
| $ \dot{Q}_{\mathrm{D}}(\tau)=h_{\mathrm{e}} A_{\mathrm{e}}\left[t_{\mathrm{e}}(\tau)-t_{\mathrm{a}}(\tau)\right]+h_{\mathrm{g}} A_{\mathrm{g}}\left[t_{\mathrm{g}}(\tau)-t_{\mathrm{a}}(\tau)\right] $ | (3) |
式中:
选取传递函数建立内热源辐射冷负荷传递函数通用模型,原因为在研究过程中,不考虑围护结构及室内固体内部复杂的蓄放热过程,而是将其看作温度均匀的一个“黑箱”,只考虑各时刻被围护结构吸收的辐射热与其冷负荷之间的数学关系。为将围护结构看作一个温度均匀的“黑箱”[17],作如下假设[18-19]:忽略围护结构各表面材质的不同,将其视为均质蓄放热固体;在同一空调环境下,认为室内各类固体(包括墙体)表面温度差别不大,即假设室内所有固体表面处于同一温度水平。
为便于研究,对室内热源作如下假设:在同一时刻,忽略内热源各表面温度的差异;在同一空调环境下,不考虑同一时刻内热源周围不同位置环境空气温度的差别;假设内热源与周围室内固体之间的相对位置和颜色等影响辐射散热过程的关键因素保持不变,即其角系数和吸收系数等辐射散热参数不随时间而变化。
因此,式(1)~(3)可简化为
| $ \dot{Q}_{\mathrm{R}}=\varepsilon \sigma_{\mathrm{b}}\left(T_{\mathrm{c}}^4-T_{\mathrm{s}}^4\right) \sum\limits_{j=1}^{n_{\mathrm{R}}} A_{\mathrm{R} j} X_{\mathrm{c}, \mathrm{s}j} $ | (4) |
| $ \dot{Q}_{\mathrm{V}}=h_{\mathrm{c}} A_{\mathrm{V}}\left(t_{\mathrm{c}}-t_{\mathrm{a}}\right)+c_{\mathrm{a}} \rho_{\mathrm{a}} q_{\mathrm{f}}\left(t_{\mathrm{f}}-t_{\mathrm{a}}\right) $ | (5) |
| $ \dot{Q}_{\mathrm{D}}(\tau)=h_{\mathrm{s}} A_{\mathrm{s}}\left[t_{\mathrm{s}}(\tau)-t_{\mathrm{a}}(\tau)\right] $ | (6) |
式中:hc为内热源表面的平均传热系数, W/(m2·℃);AV为内热源表面总对流散热面积,m2;tc为内热源表面平均温度,℃;Xc, sj为内热源表面j与围护结构及室内固体表面的总体角系数;Tc为内热源表面平均热力学温度,K;Ts为室内固体与围护结构的平均热力学温度,K。
为建立内热源滞后冷负荷在线监测模型,分别以室内空气、室内固体及围护结构为研究对象,建立其能量守恒方程。围护结构及室内固体表面与内热源之间的散热过程包括两个部分:围护结构及室内固体表面与内热源表面间的辐射散热过程;在吸收一定量的内热源辐射热后,围护结构及室内固体表面与室内空气之间形成温差,从而引起对流散热过程。
因此,室内固体及围护结构传热模型如式(7)所示:
| $ c_{\mathrm{s}} \rho_{\mathrm{s}} V_{\mathrm{s}} \frac{\mathrm{~d} t_{\mathrm{s}}}{\mathrm{~d} \tau}=\dot{Q}_{\mathrm{R}}+h_{\mathrm{s}} A_{\mathrm{s}}\left(t_{\mathrm{a}}-t_{\mathrm{s}}\right) $ | (7) |
式中:cs为室内固体与围护结构的平均比热容,J/(kg·℃);ρs为室内固体与围护结构的平均密度,kg/m3;Vs为室内固体与围护结构的整体体积,m3;ts为室内固体与围护结构的平均温度,℃;hs为室内固体与围护结构表面的平均对流换热系数, W/(m2·℃); As为室内固体与围护结构的整体表面积,m2。
不失一般性,在建立室内空气传热模型时,将受迫对流部分考虑进来。室内空气因内热源而产生的热传递过程由3部分组成:内热源与室内空气之间的自然对流换热过程;围护结构及室内固体在蓄热后,辐射热以自然对流方式进入室内空气;内热源与室内空气之间的受迫对流换热过程(如电脑散热风扇与室内空气之间的对流散热过程)。
在不考虑室外气象条件、冷风侵入和冷风渗透等外部环境影响的情况下,根据能量守恒原理,室内空气的传热模型如式(8)所示:
| $ \dot{Q}_{\mathrm{v}}-h_{\mathrm{s}} A_{\mathrm{s}}\left(t_{\mathrm{a}}-t_{\mathrm{s}}\right)=c_{\mathrm{a}} \rho_{\mathrm{a}} V_{\mathrm{a}} \frac{\mathrm{~d} t_{\mathrm{a}}}{\mathrm{~d} \tau} $ | (8) |
式中Va为受内热源散热过程影响的空气体积,m3。
为简化计算过程,提高模型精度,采用拉式变换对上述模型进行处理。拉氏变换是一种线性变换,可将函数的实数参数t(t≥0)转换为复数参数s[16]。本质上,拉氏变换是一种处理函数的函数,只要给定一个时域函数(信号),就能通过拉式变换得到一个复频域信号,因而,只要对这个复频域信号进行处理,也就相当于对时域信号进行处理。拉式变换可以将微分方程转变为代数方程,从而大幅简化计算过程,对传递函数模型的推导过程意义重大。
对式(4)~(8)进行拉氏变换得
| $ \begin{aligned} \bar{Q}_{\mathrm{R}}= & \varepsilon \sigma_{\mathrm{b}} X_{\mathrm{c}, \mathrm{~s}} A_{\mathrm{c}}\left(\frac{273^4}{s}+\frac{4 \times 273^3}{s^2}+\frac{12 \times 273^2}{s^3}+\right. \\ & \left.\frac{24 \times 273}{s^4}\right)\left[\theta_{\mathrm{c}}(s)-\theta_{\mathrm{s}}(s)\right] \end{aligned} $ | (9) |
| $ \bar{Q}_{\mathrm{V}}=c_{\mathrm{a}} \rho_{\mathrm{a}} q_{\mathrm{f}}\left[\theta_{\mathrm{f}}(s)-\theta_{\mathrm{a}}(s)\right]+h_{\mathrm{c}} A_{\mathrm{V}}\left[\theta_{\mathrm{c}}(s)-\theta_{\mathrm{a}}(s)\right] $ | (10) |
| $ \bar{Q}_{\mathrm{R}}=s \rho_{\mathrm{s}} V_{\mathrm{s}} c_{\mathrm{s}} \theta_{\mathrm{s}}(s)-h_{\mathrm{s}} A_{\mathrm{s}}\left[\theta_{\mathrm{a}}(s)-\theta_{\mathrm{s}}(s)\right] $ | (11) |
| $ \bar{Q}_{\mathrm{v}}=s \rho_{\mathrm{a}} V_{\mathrm{a}} c_{\mathrm{a}} \theta_{\mathrm{a}}(s)+h_{\mathrm{s}} A_{\mathrm{s}}\left[\theta_{\mathrm{a}}(s)-\theta_{\mathrm{s}}(s)\right] $ | (12) |
| $ \bar{Q}_{\mathrm{D}}(s)=h_{\mathrm{s}} A_{\mathrm{s}}\left[\theta_{\mathrm{s}}(s)-\theta_{\mathrm{a}}(s)\right] $ | (13) |
对于小部分有受迫对流的内热源(如带风扇散热系统的电脑),假设内热源表面与受迫对流空气处于同一温度水平,式(10)可以简化为
| $ \bar{Q}_{\mathrm{V}}=\left(c_{\mathrm{a}} \rho_{\mathrm{a}} q_{\mathrm{f}}+h_{\mathrm{c}} A_{\mathrm{V}}\right)\left[\theta_{\mathrm{c}}(s)-\theta_{\mathrm{a}}(s)\right] $ | (14) |
联立式(9)、(11)~(14)得
| $ \theta_{\mathrm{a}}(s)=\frac{b_{\mathrm{a} 0} s^5+b_{\mathrm{a} 1} s^4+b_{\mathrm{a} 2} s^3+b_{\mathrm{a} 3} s^2+b_{\mathrm{a} 4} s+b_{\mathrm{a} 5}}{a_{\mathrm{a} 0} s^5+a_{\mathrm{a} 1} s^4+a_{\mathrm{a} 2} s^3+a_{\mathrm{a} 3} s^2+a_{\mathrm{a} 4} s+a_{\mathrm{a} 5}} \theta_{\mathrm{c}}(s) $ | (15) |
式中:aa0~aa5, ba0~ba5解析解详见附录A。式(15)中的高阶次项是由辐射热计算公式中的4阶温度参数所导致,且该阶次在后续推导过程中逐渐升高,最后演变为aa0及ba0的5阶次。根据aa0~aa5, ba0~ba5解析解可知,θa(s)受内热源参数、空气参数及围护结构参数影响,如内热源表面传热系数、表面积及温度等。相对分子参数ba0~ba5,分母参数aa0~aa5的数值主要取决于围护结构和室内固体相关参数,如密度、体积和表面温度等。
联立式(9)、(11)~(14)得
| $ \theta_{\mathrm{s}}(s)=\frac{b_{\mathrm{s} 0} s^4+b_{\mathrm{s} 1} s^3+b_{\mathrm{s} 2} s^2+b_{\mathrm{s} 3} s+b_{\mathrm{s} 4}}{a_{\mathrm{s} 0} s^5+a_{\mathrm{s} 1} s^4+a_{\mathrm{s} 2} s^3+a_{\mathrm{s} 3} s^2+a_{\mathrm{s} 4} s+a_{\mathrm{s} 5}} \theta_{\mathrm{c}}(s) $ | (16) |
式中:as0~as5, bs0~bs4解析解详见附录A。式(16)中的高阶次项as0及bs0同样是由辐射热计算公式中的4阶温度参数导致。对as0~as5, bs0~bs4解析解分析可知,θa(s)数值主要取决于内热源表面传热系数及对流换热面积数值的大小,而θs(s)在其基础上,还受围护结构及室内固体表面积及传热系数的影响。
联立式(7)、(9)~(13),得到单个内热源滞后冷负荷监测模型,即
| $ G_{\mathrm{D}}(s)=\frac{\bar{Q}_{\mathrm{D}}(s)}{\bar{Q}_{\mathrm{R}}(s)}=\frac{b_{\mathrm{D} 0} s^{10}+b_{\mathrm{D} 1} s^9+b_{\mathrm{D} 2} s^8+b_{\mathrm{D} 3} s^7+b_{\mathrm{D} 4} s^6+b_{\mathrm{D} 5} s^5+b_{\mathrm{D} 6} s^4+b_{\mathrm{D} 7} s^3+b_{\mathrm{D} 8} s^2+b_{\mathrm{D} 9} s+b_{\mathrm{D} 10}}{a_{\mathrm{D} 0} s^{10}+a_{\mathrm{D} 1} s^9+a_{\mathrm{D} 2} s^8+a_{\mathrm{D} 3} s^7+a_{\mathrm{D} 4} s^6+a_{\mathrm{D} 5} s^5+a_{\mathrm{D} 6} s^4+a_{\mathrm{D} 7} s^3+a_{\mathrm{D} 8} s^2+a_{\mathrm{D} 9} s+a_{\mathrm{D} 10}} $ | (17) |
式中:aD0~aD10, bD0~bD10详见附录B。
由式(17)可知,内热源滞后冷负荷监测模型的理论推导结果为10阶传递函数,该模型的高阶次是由辐射散热量计算模型中的4阶次温度参数引起,且该阶次在后续公式推导过程中逐渐升高至10阶。传递函数GD(τ)(s)表达s域的内热源辐射冷负荷与其辐射散热量之比,即τ时刻从围护结构及室内固体进入空气的热量与内热源辐射散热量之比,该时刻进入空气的热量包含0~τ时段内所有被吸收的辐射热在该时刻进入室内空气的部分。所以,模型结果主要受围护结构蓄放热特性影响,影响参数包括窗墙比、有无地毯等。
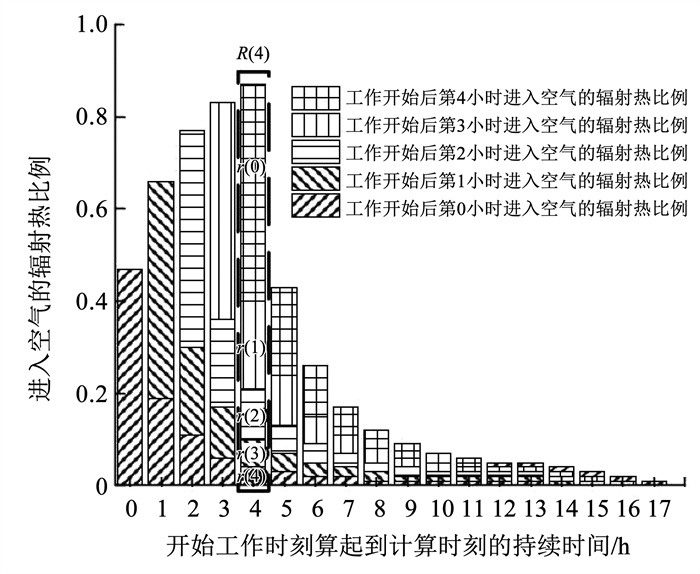
2 滞后冷负荷传递函数模型参数辨识及降阶分析 2.1 模型的参数辨识在式(17)的解析解中,部分参数的数值很难确定,因此,采取参数辨识方法获取滞后冷负荷传递函数模型中的未知参数。在辨识过程中,引用了ASHRAE手册中给出的辐射时间系数。根据辐射时间系数的定义,在内热源工作工况下,τ时刻内热源滞后冷负荷为Qr(τ)r(0)+Qr(τ-1)r(1)+…+Qr(0)r(τ)[8]。围护结构在吸收内热源辐射热的同时,也在向周围环境散热,围护结构蓄热量由蓄热与放热的差值决定。内热源停止工作或离开房间后,对流及辐射散热过程停止,但是,内热源对室内热环境的影响还未停止,围护结构放热过程仍在继续。以工作4 h的内热源为例,总结其逐时进入空气的辐射热比例,如图 3所示。在某研究时段内,内热源滞后冷负荷包含前面所有工作时段内被吸收的辐射热在该时段进入空气的部分,该现象导致散热量与冷负荷之间存在时间延迟和幅度衰减。因此,研究室内热源逐时冷负荷的关键在于由辐射热引起的滞后冷负荷部分。
|
图 3 逐时进入空气的内热源辐射热比例 Fig. 3 Hourly proportion of radiant heat from internal heat sources entering air |
根据ASHRAE手册[8],τ时刻某一内热源辐射散热量引起的冷负荷计算公式为
| $ \begin{gathered} \dot{Q}_{\mathrm{D}}(\tau)=r(0) \dot{Q}_{\mathrm{r}}(\tau)+r(1) \dot{Q}_{\mathrm{r}}(\tau-1)+ \\ r(2) \dot{Q}_{\mathrm{r}}(\tau-2)+\cdots+r(23) \dot{Q}_{\mathrm{r}}(\tau-23)= \\ \sum\limits_{i=0}^{23} r(i) \dot{Q}_{\mathrm{r}}(\tau-i) \end{gathered} $ | (18) |
式中:
| $ \begin{gathered} \dot{Q}_{\mathrm{D}}(\tau)=r(0) \dot{Q}_{\mathrm{r}}(\tau)+r(1) \dot{Q}_{\mathrm{r}}(\tau-1)+ \\ r(2) \dot{Q}_{\mathrm{r}}(\tau-2)+\cdots+r(0) \dot{Q}_{\mathrm{r}}(\tau)= \\ \sum\limits_{i=0}^\tau r(i) \dot{Q}_{\mathrm{r}}(\tau-i) \end{gathered} $ | (19) |
由式(18)、(19)可知,对于工作n h(0 ≤n≤23)的内热源,其辐射散热量引起的冷负荷在工作时段和非工作时段如式(20)~(22)所示。
对于工作时段
| $ \left[\begin{array}{c} \dot{Q}_{\mathrm{D}}(0) \\ \dot{Q}_{\mathrm{D}}(1) \\ \vdots \\ \dot{Q}_{\mathrm{D}}(n) \end{array}\right]=\left[\begin{array}{cccc} r(0) & & & \\ r(0) & r(1) & & \\ \vdots & \vdots & & \\ r(0) & r(1) & \cdots & r(n) \end{array}\right]\left[\begin{array}{cccc} \dot{Q}_{\mathrm{R}}(0) & \dot{Q}_{\mathrm{R}}(1) & \cdots & \dot{Q}_{\mathrm{R}}(n) \\ & \dot{Q}_{\mathrm{R}}(0) & \cdots & \dot{Q}_{\mathrm{R}}(n-1) \\ & & \cdots & \vdots \\ & & & \dot{Q}_{\mathrm{R}}(0) \end{array}\right] $ | (20) |
对于非工作时段(从结束工作时刻至23时)
| $ \left[\begin{array}{c} \dot{Q}_{\mathrm{D}}(n+1) \\ \dot{Q}_{\mathrm{D}}(n+2) \\ \vdots \\ \dot{Q}_{\mathrm{D}}(23) \end{array}\right]=\left[\begin{array}{cccc} r(1) & r(2) & \cdots & r(n+1) \\ r(2) & r(3) & \cdots & r(n+2) \\ \vdots & \vdots & \vdots & \vdots \\ r(23-n) & r(24-n) & \cdots & r(23) \end{array}\right]\left[\begin{array}{cccc} \dot{Q}_{\mathrm{R}}(n) & \dot{Q}_{\mathrm{R}}(n) & \cdots & \dot{Q}_{\mathrm{R}}(n) \\ \dot{Q}_{\mathrm{R}}(n-1) & \dot{Q}_{\mathrm{R}}(n-1) & \cdots & \dot{Q}_{\mathrm{R}}(n-1) \\ \vdots & \vdots & \vdots & \vdots \\ \dot{Q}_{\mathrm{R}}(0) & \dot{Q}_{\mathrm{R}}(0) & \cdots & \dot{Q}_{\mathrm{R}}(0) \end{array}\right] $ | (21) |
对于非工作时段(从第2日0时至第2日24-n时)
| $ \left[\begin{array}{c} \dot{Q}_{\mathrm{D}}(24) \\ \dot{Q}_{\mathrm{D}}(25) \\ \vdots \\ \dot{Q}_{\mathrm{D}}(23+n) \end{array}\right]=\left[\begin{array}{ccccc} r(24-n) & r(25-n) & \cdots & r(22) & r(23) \\ r(25-n) & r(26-n) & \cdots & r(23) & \\ \vdots & \vdots & \vdots & & \end{array}\right]\left[\begin{array}{ccccc} \dot{Q}_{\mathrm{R}}(n) & \dot{Q}_{\mathrm{R}}(n) & \cdots & \dot{Q}_{\mathrm{R}}(n) & \dot{Q}_{\mathrm{R}}(n) \\ \dot{Q}_{\mathrm{R}}(n-1) & \dot{Q}_{\mathrm{R}}(n-1) & \cdots & \dot{Q}_{\mathrm{R}}(n-1) & \\ \vdots & \vdots & \vdots & \\ \dot{Q}_{\mathrm{R}}(1) & & & \end{array}\right] $ | (22) |
内热源在开始工作后的1 h内辐射散热量都达到稳定状态。若照明及电子电气类设备工作状态无较大波动,则辐射散热量数值一直处于稳定状态[13,20]。人员皮肤表面温度稳定在36~37 ℃,若其衣着和行为特性无大幅变化,人体辐射散热量同样处于稳定状态。为便于计算,认为
| $ \dot{Q}_{\mathrm{R}}(0)=\dot{Q}_{\mathrm{R}}(1)=\cdots=\dot{Q}_{\mathrm{R}}(n-1)=\dot{Q}_{\mathrm{R}}(n) $ | (23) |
因此,式(19)可简化为
| $ \dot{Q}_{\mathrm{D}}(\tau)=\dot{Q}_{\mathrm{R}} R(\tau) $ | (24) |
将R(τ)命名为τ时刻总辐射时间系数,表示τ时刻的滞后冷负荷与该时刻辐射散热量的比值。利用总辐射时间系数对内热源滞后冷负荷监测模型进行参数辨识,原因如下:
1)从围护结构蓄放热角度和内热源滞后冷负荷形成角度,R(τ)与GD(τ)具有相同的物理意义。相对各时刻的辐射时间系数ri,总辐射时间系数R(τ)考虑了时间的叠加效果,可以体现出自0~τ时刻整个工作时段内,各个时刻被吸收的辐射热在τ时刻进入室内空气形成滞后冷负荷的比例之和,与GD(τ)表达的物理意义吻合。
2)从数学角度分析,R(τ)与GD(τ)具有一致的数学表达形式。式(17)可表示为式(25),由于复数域内的乘法等效于时域内的卷积[21],式(25)可以表达为卷积积分形式,如式(26)所示。卷积是两个变量在某范围内相乘后求和的结果,如果卷积的变量是序列GD(τ)和
| $ \bar{Q}_{\mathrm{D}(\tau)}(s)=G_{\mathrm{D}}(s) \times \bar{Q}_{\mathrm{R}(\tau)}(s) $ | (25) |
| $ \dot{Q}_{\mathrm{D}}(\tau)=\int_0^\tau G_{\mathrm{D}}(t) \times \dot{Q}_{\mathrm{R}}(\tau-t) \mathrm{d} t $ | (26) |
| $ \dot{Q}_{\mathrm{D}}(\tau)=\dot{Q}_{\mathrm{R}}(\tau) \times G_{\mathrm{D}}(\tau) $ | (27) |
| $ \dot{Q}_{\mathrm{D}}(\tau)=\dot{Q}_{\mathrm{R}} \times G_{\mathrm{D}}(\tau) $ | (28) |
在应用R(τ)对内热源滞后冷负荷监测模型进行参数辨识之前,需通过如下步骤获取R(τ)的具体数值并对其进行处理:
1)根据式(20)~(22)得出工作与非工作时段内R(τ)计算方法,如式(29)所示。
| $ R(\tau)=\left\{\begin{array}{l} \sum\limits_{k=0}^\tau r(k), 0 \leqslant \tau \leqslant n \\ \sum\limits_{k=\tau-n}^\tau r(k), n \leqslant \tau \leqslant 23 \\ \sum\limits_{k=\tau-n}^{23} r(k), 24 \leqslant \tau \leqslant n+23 \end{array}\right. $ | (29) |
2)利用ASHRAE手册[8]中给出的典型围护结构辐射时间系数(附录A),并结合式(29),得出某类型围护结构(轻型墙体,有地毯,窗墙比10%)24 h总辐射时间系数,如附录B所示。围护结构类型划分方式如表 1所示。
3)在内热源滞后冷负荷监测模型参数辨识过程中,需对连续型传递函数进行离散化处理。虽然相关书籍[1-2]、模拟软件(例如TRNSYS)中将内热源冷负荷时间步长取为1 h进行计算,但是该步长很难全面、详细地描述内热源冷负荷动态变化特性。本研究将内热源滞后冷负荷传递函数计算模型时间步长设置为5 min。
4)由附录B可知,利用ASHRAE手册数据计算所得总辐射时间系数时间间隔为1 h,为获取每5 min的总辐射时间系数,建立各类围护结构总辐射时间系数变化曲线,以5 min为时间间隔进行取值,并将其代入辨识过程。
内热源滞后冷负荷监测模型参数辨识步骤如下:
1)将内热源滞后冷负荷监测模型(式(17))转化为差分方程。
2)将某类型围护结构(轻型墙体,有地毯,窗墙比10%)总辐射时间系数代入差分方程,构成一个线性方程组。
3)利用最小二乘法,解得线性方程中的近似解,并将其转化为离散型传递函数,如式(30)所示。式中参数a′D1~a′D10、b′D0~b′D10可通过上述参数辨识方法获取。
| $ G_{\mathrm{D}}(z)=\frac{\bar{Q}_{\mathrm{D}(\tau)}(z)}{\bar{Q}_{\mathrm{R}}(z)}=\frac{b_{\mathrm{D} 0}^{\prime}+b_{\mathrm{D} 1}^{\prime} z^{-1}+b_{\mathrm{D} 2}^{\prime} z^{-2}+b_{\mathrm{DD}}^{\prime} z^{-3}+b_{\mathrm{D} 4}^{\prime} z^{-4}+b_{\mathrm{D} 5}^{\prime} z^{-5}+b_{\mathrm{D} 0}^{\prime} z^{-6}+b_{\mathrm{D} 7}^{\prime} z^{-7}+b_{\mathrm{D} 8}^{\prime} z^{-8}+b_{\mathrm{D} 9}^{\prime} z^{-9}+b_{\mathrm{D} 1}^{\prime} z^{-10}}{1+a_{\mathrm{D} 1}^{\prime} z^{-1}+a_{\mathrm{D} 2}^{\prime} z^{-2}+a_{\mathrm{D} 3}^{\prime} z^{-3}+a_{\mathrm{D} 4}^{\prime} z^{-4}+a_{\mathrm{D} 5}^{\prime} z^{-5}+a_{\mathrm{D} 6}^{\prime} z^{-6}+a_{\mathrm{D} 7}^{\prime} z^{-7}+a_{\mathrm{D} 8}^{\prime} z^{-8}+a_{\mathrm{D} 9}^{\prime} z^{-9}+a_{\mathrm{D} 10}^{\prime} z^{-10}} $ | (30) |
由式(30)可知,内热源滞后冷负荷监测模型推导结果为10阶函数,该模型形式较复杂,在增加计算时间的同时,很难保证计算精度。为提高模型在实际工况下的应用性,需对其进行降阶简化处理,具体步骤如下:
1) 将式(30)的阶次分别降为9阶,8阶,…,1阶。
2)利用上述参数辨识方法得出各阶次模型中的未知参数。
3)对各阶次传递函数计算模型的精度及结构进行对比分析。
不同阶次的模型在参数辨识过程中运用最小二乘法,并选取平均绝对百分比误差EMAP(mean absolute percentage error)和绝对百分比误差EAP(absolute percentage error)对模型精度进行评价,其计算方法如式(31)和(32)所示,以EMAP最低的辨识结果作为模型参数。
| $ E_{\mathrm{MAP}}=\frac{1}{n} \sum\limits_{i=1}^n \frac{\left|\dot{Q}_{\mathrm{D} i}-\dot{Q}_{\mathrm{D} i}^{\prime}\right|}{\dot{Q}_{\mathrm{D} i}} $ | (31) |
| $ E_{\mathrm{AP}}=\frac{\left|\dot{Q}_{\mathrm{D} i}-\dot{Q}_{\mathrm{D} i}^{\prime}\right|}{\dot{Q}_{\mathrm{D} i}} $ | (32) |
式中:
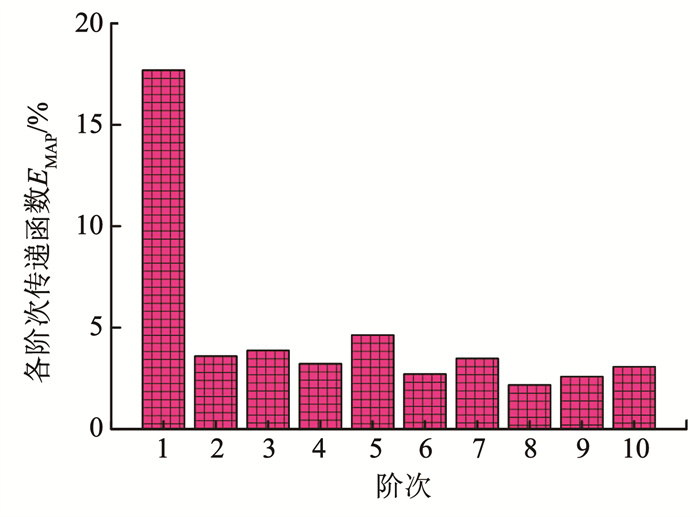
图 4中的EMAP为各阶次模型辨识过程中EMAP最低值,即辨识结果所对应的精度。当连续型传递函数模型阶次大于2时,离散化后的模型EMAP小于5%。因为2阶传递函数计算模型结构较简单,可以降低计算时间和误差,相对其他阶次的模型实际工况下应用性更高,在内热源滞后冷负荷的计算过程选取2阶传递函数模型,其结构如式(33)所示:
| $ G_{\mathrm{D}}(z)=\frac{b_{\mathrm{D} 0}^{\prime}+b_{\mathrm{D} 1}^{\prime} z^{-1}+b_{\mathrm{D} 2}^{\prime} z^{-2}}{1+a_{\mathrm{D} 1}^{\prime} z^{-1}+a_{\mathrm{D} 2}^{\prime} z^{-2}} $ | (33) |
|
图 4 各阶次传递函数EMAP柱状示意 Fig. 4 EMAP value column diagram of transfer functions with different order |
随后,利用相同的参数辨识及模型降阶方法,求出应用于其他典型围护结构的内热源滞后冷负荷监测模型参数,模型参数如附录C所示。
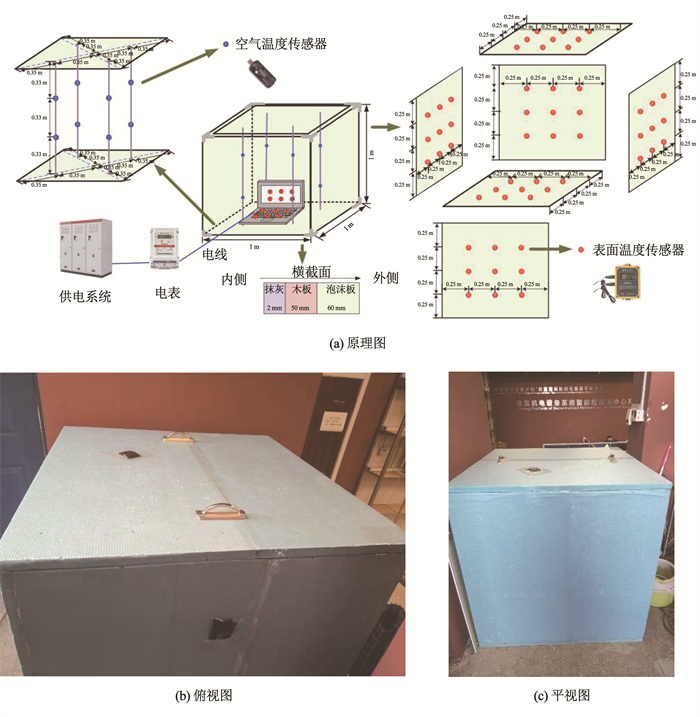
3 模型验证分析 3.1 试验系统的设计、建立及调试 3.1.1 试验系统的设计及建立通过试验方式验证模型精度,试验系统原理及外观如图 5所示。试验系统尺寸为1 m×1 m×1 m,呈正方体形状,容积为1 m3。为减少外界热源及热环境对试验过程的影响,试验系统横截面共由3层材料组成,分别为2 mm的抹灰层、50 mm的木板层和60 mm的泡沫板层。根据式(34)[23],试验系统材料传热系数为0.11 W/(m2 · K)。同时,试验系统各个面之间的缝隙用隔热密封胶粘连,最大程度降低由试验系统缝隙造成的热损失。在试验箱内侧设置抹灰层是为模拟实际围护结构材料,从而模仿室内热源实际工况下与围护结构之间的热传递过程,提高试验结果可靠性。试验系统可以连接供电系统,为试验设备进行电能供应。
| $ k_{\mathrm{ch}}=\frac{1}{\frac{1}{h_{\mathrm{Pl}}}+\frac{\delta_{\mathrm{Pl}}}{K_{\mathrm{Pl}}}+\frac{\delta_{\mathrm{W}_{\mathrm{o}}}}{K_{\mathrm{W}_{\mathrm{o}}}}+\frac{\delta_{\mathrm{Fo}}}{K_{\mathrm{Fo}}}+\frac{1}{h_{\mathrm{Fo}}}} $ | (34) |
|
图 5 试验系统示意 Fig. 5 Diagram of experimental system |
式中:kch为试验系统材料传热系数,W/(m2 · K);KPl,KWo,KFo分别为抹灰层、模板层和泡沫层的导热系数,W/(m · K);δPl,δWo,δFo分别为抹灰层、模板层和泡沫层的厚度,m;hPl和hFo分别为表面传热系数,W/(m2 · K)。
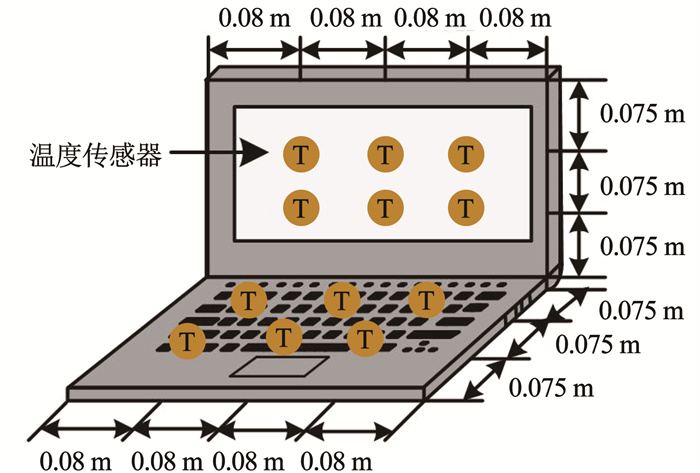
根据上文分析可知,需要测量的温度参数有两种,即空气温度和试验系统内壁面温度。由于绝热方舱试验系统内部空气温度具有不均匀性,为提高测量精度,在其内部均匀设置多个测点,以消除不均匀温度带来的试验误差。均匀地在箱内放置4条线,每条线的0.33 m和0.66 m高度位置分别放置两个温度传感器,并采用8个测点温度平均值作为试验箱空气温度值。绝热方舱内壁面的温度分布也具有不均匀性,故在方舱每个内壁面均匀地放置9个温度测点,并在计算过程中采用温度平均值。选用CPU型号为i5-9300H、GPU型号为NVIDIA GeForce GTX 960的电脑作为试验热源,为降低电脑表面温度不均匀性带来的误差,在试验电脑每个表面设置3~6个温度传感器,如图 6所示。在散热量计算过程中,选取温度测量数据的平均值。
|
图 6 笔记本电脑传感器位置 Fig. 6 Installation locations of test laptop sensors |
选取四路温度记录仪(型号为ADR-41)测量绝热系统内壁面温度,Apresys U盘式温湿度记录仪计量试验箱内部空气温度。试验前使用温度检定箱对两种传感器进行校准,所使用的设备规格如表 2所示。为保证参数的一致性,根据试验设备表面温度变化特征,将所有空气温度、试验系统内壁面温度采样周期全部设置为1 h。
| 表 2 试验设备及其规格 Tab. 2 Specifications of equipment adopted in experiment |
对试验系统进行调试及误差分析,具体内容如下:
1)试验系统试运行。在试验开始前需要对试验系统进行试运行调试,从而保证试验过程中试验系统可靠、安全和稳定地运行。首先,检查试验设备是否在通电状态下正常运转,其次,检查传感器能否正常使用,最后,检查电表读数是否正常。
2)误差分析。对式(4)和(6)取对数,进行微分可得内热源辐射热及滞后冷负荷的误差计算方法,如式(35)和(36)。结合公式与试验数据可知,辐射散热及滞后冷负荷的误差分别在±3.87%和±4.65%以内。
| $ \frac{\delta \dot{Q}_{\mathrm{R}}}{\dot{Q}_{\mathrm{R}}}=\sqrt{\left[\frac{4 \varepsilon \sigma_{\mathrm{b}} X_{\mathrm{c}, \mathrm{~s}} A_{\mathrm{R}} T_{\mathrm{c}}^4}{\varepsilon \sigma_{\mathrm{b}} X_{\mathrm{c}, \mathrm{~s}} A_{\mathrm{R}}\left(T_{\mathrm{c}}^4-T_{\mathrm{s}}^4\right)}\left(\frac{\delta T_{\mathrm{c}}}{T_{\mathrm{c}}}\right)\right]^2+\left[\frac{4 \varepsilon \sigma_{\mathrm{b}} X_{\mathrm{c}, \mathrm{~s}} A_{\mathrm{R}} T_{\mathrm{s}}^4}{\varepsilon \sigma_{\mathrm{b}} X_{\mathrm{c}, \mathrm{~s}} A_{\mathrm{R}}\left(T_{\mathrm{c}}^4-T_{\mathrm{s}}^4\right)}\left(\frac{\delta T_{\mathrm{s}}}{T_{\mathrm{s}}}\right)\right]^2} $ | (35) |
| $ \frac{\delta \dot{Q}_{\mathrm{D}}}{\dot{Q}_{\mathrm{D}}}=\sqrt{\left[\frac{t_{\mathrm{e}}}{t_{\mathrm{e}}-t_{\mathrm{a}}}\left(\frac{\delta t_{\mathrm{e}}}{t_{\mathrm{e}}}\right)\right]^2+\left[\frac{t_{\mathrm{a}}}{t_{\mathrm{e}}-t_{\mathrm{a}}}\left(\frac{\delta t_{\mathrm{a}}}{t_{\mathrm{a}}}\right)\right]^2} $ | (36) |
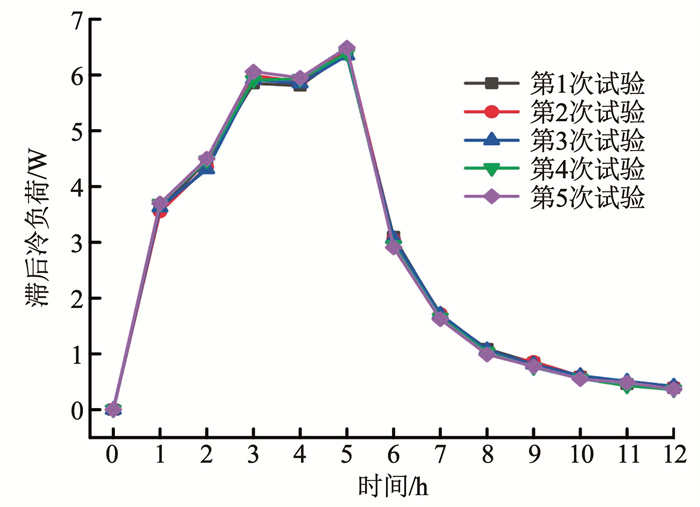
3)可重复性分析。试验的可重复性分析目的是检验试验系统在不同的时间段内,能否重复同一工况下的试验结果。在试运行过程中,选取一台电脑于不同日期重复试验5次,每次工作时间为5 h。5次试验的滞后冷负荷数据如图 7所示。5次试验中,同一时段滞后冷负荷最大值与最小值的绝对百分比误差在2.2%~8.3%。
|
图 7 可重复性分析结果 Fig. 7 Results of repeatability analysis |
通过式(3)获取内热源滞后冷负荷试验数据,公式中涉及的参数及获取方法分别为:温度参数,试验测量得到;试验系统内壁面表面传热系数,通过查阅文献[15]获取;试验系统内壁面表面积,利用尺寸参数结合矩形面积公式计算。
为获取滞后冷负荷模型计算结果,首先,利用式(1)计算试验电脑辐射散热量,然后,利用辐射散热量与式(33)计算得到。式(1)中涉及的参数及获取方法分别为:试验电脑表面法向发射率和黑体辐射常数,通过查阅文献[15]获取;试验电脑表面与试验系统内壁面之间的角系数,由电脑尺寸与试验系统尺寸结合角系数公式计算得出。
研究热源工作5 h的情况下,其滞后冷负荷的数值规律。首先,利用试验数据及式(1)、(3)获取热源辐射散热量及滞后冷负荷试验结果。然后,根据式(33)和热源辐射散热量得出内热源滞后冷负荷模型计算结果。模型验证结果如图 8所示,EAP在2.07%~17.06%波动,EMAP为8.19%。

|
图 8 内热源滞后冷负荷监测模型验证结果 Fig. 8 Verification results of radiant cooling load model of internal heating sources |
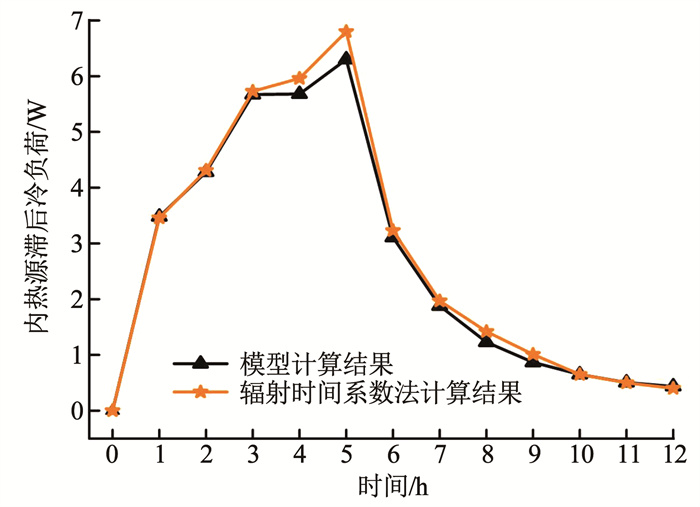
ASHRAE协会给出的内热源滞后冷负荷计算方法(即辐射时间系数法)在世界范围广泛应用[22],为验证模型精度,在上述试验工况下对辐射时间系数法与本文模型进行精度对比分析。基于式(1)、(18)、辐射时间系数及试验数据,分别计算得出0~12 h的滞后冷负荷数据。将辐射时间系数法计算结果与模型结果进行对比(如图 9所示),模型的EMAP为4.62%。
|
图 9 内热源滞后冷负荷监测模型验证结果 Fig. 9 Verification results of radiant cooling load model of internal heating sources |
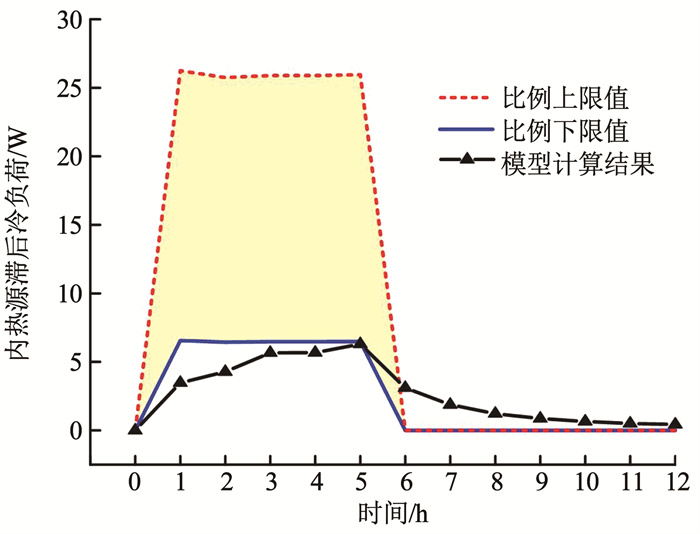
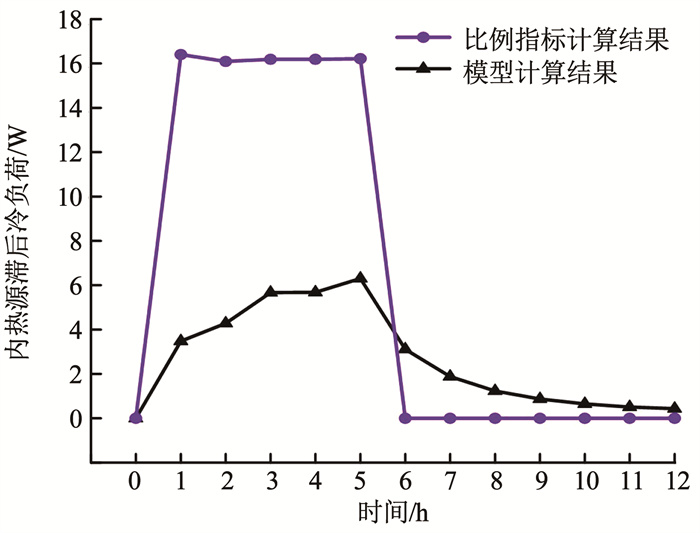
从时间延迟效果、计算精度、应用前景角度对建立的内热源滞后冷负荷监测模型进行讨论。以工作5 h的试验电脑为研究对象,首先,引用试验数据和实时电功率法[4]得出其实时冷负荷。然后,分别利用Spitler等[11]提出的电脑类设备滞后冷负荷比例范围、Hosni等[12]提出的滞后冷负荷比例指标值计算试验电脑滞后冷负荷
|
图 10 模型与文献[11]计算结果对比分析 Fig. 10 Comparison and analysis diagram of calculation results between developed model and Reference[11] |
|
图 11 模型与文献[12]计算结果对比分析 Fig. 11 Comparison and analysis diagram of calculation results between developed model and Reference[12] |
1)时间延迟效果。由模型计算结果可知,在试验设备工作期间,
2)计算精度。在试验设备工作工况下,滞后冷负荷比例上、下限值的EMAP分别为416.08%、29.02%,比模型计算结果高407.89%、20.83%。同时,比例指标值计算结果的EMAP比模型计算结果高214.36%。相对受人员主观思想影响的调查问卷法[5-6],模型结果更贴近内热源实际负荷情况,计算精度更高。提高内热源实时冷负荷的计算精度对于指导供暖空调系统节能调控、促进建筑智慧运维具有重要意义。
3)应用前景。相对辐射时间系数法[8],内热源滞后冷负荷监测模型计算过程较为便捷,输入参数只有逐时辐射散热量,而辐射时间系数法[8]需要参考48个参数才能获取某一时刻的冷负荷数值。内热源滞后冷负荷监测模型可以依托能耗监测平台[24]实现数据的在线获取,相比投入大量人力物力的调查问卷法[5-6]和摄像法[3],该模型具有更好的应用前景。
在建立模型过程中,为便于计算,假设辐射得热会瞬间均匀地存储在蓄热体内,然而在实际工况下,只有表面少部分材料会吸收辐射热,升高温度后向室内传递热量。尽管该假设会对计算精度产生一定影响,但从节约计算资源、降低模型结构复杂度、提高模型应用性等方面综合考虑,最终选择保留该假设。内热源滞后冷负荷监测模型的适用范围为装配能耗监测系统的建筑。在实际应用中,为减少室外环境影响,模型更适用于热阻较大的外围护结构及建筑内围护结构。
5 结论基于围护结构蓄放热动态分析、热传递规律、拉氏变换原理等建立内热源滞后冷负荷在线监测模型,该模型为描述滞后冷负荷时间延迟及幅度衰减特性提供理论依据。基于辐射时间系数,对模型进行了参数辨识及降阶分析,对简化计算过程,促进供暖空调系统节能调控具有理论意义。主要结论如下:
1)内热源滞后冷负荷监测模型的理论推导结果为10阶传递函数。
2)对模型进行参数辨识及降阶分析过程中,2~10阶模型的EMAP皆小于5%,降阶分析后得到2阶离散型传递函数。
3)利用试验结果验证模型的过程中,模型的EAP在2.07%~17.06%波动,EMAP为8.19%。利用辐射时间系数法验证模型的过程中,模型的EMAP为4.62%。
4)与现有研究相比,内热源滞后冷负荷监测模型的EMAP提高了20.83%~407.89%,模型计算过程更加便捷,并且可依托能耗监测平台实现内热源滞后冷负荷的在线获取。同时,模型可以描述热源在工作与非工作时段的时间延迟效果,计算结果在停止工作后的第1小时就达到0 W,而本文模型计算结果在7 h后才降至0 W。
附录A| 表 A1 典型围护结构辐射时间系数 Tab. A1 Radiant time factors of typical building envelope |
| 表 B1 某类型围护结构总辐射时间系数 Tab. B1 Radiant time factors of a building envelope |
| 表 C1 内热源滞后冷负荷监测模型参数 Tab. C1 Parameters of radiant cooling load monitoring models of internal heat sources |
| [1] |
陆耀庆. 实用供热空调设计手册[M]. 2版. 北京: 中国建筑工业出版社, 2008. LU Yaoqing. Practical heating and air conditioning design manual[M]. 2nd ed. Beijing: China Architecture & Building Press, 2008. |
| [2] |
陆亚俊, 马最良, 邹平华. 暖通空调[M]. 3版. 北京: 中国建筑工业出版社, 2015. LU Yajun, MA Zuiliang, ZOU Pinghua. Heating, ventilation, and air-conditioning[M]. 3rd ed. Beijing: China Architecture & Building Press, 2015. |
| [3] |
WEI S, TIEN P W, CALAUTIT J K, et al. Vision-based detection and prediction of equipment heat gains in commercial office buildings using a deep learning method[J]. Applied Energy, 2020, 277: 115506. DOI:10.1016/j.apenergy.2020.115506 |
| [4] |
AN Jingjing, YAN Da, HONG Tianzhen, et al. A novel stochastic modeling method to simulate cooling loads in residential districts[J]. Applied Energy, 2017, 206: 134. DOI:10.1016/j.apenergy.2017.08.038 |
| [5] |
YANG Dongsheng, YAO Qi, JIA Mintao, et al. Application analysis of efficient heat dissipation of electronic equipment based on flexible nanocomposites[J]. Energy Built Environment, 2021, 2(2): 157. DOI:10.1016/j.enbenv.2020.07.008 |
| [6] |
SARFRAZ O, BACH C K. Update to office equipment diversity and load factors (ASHRAE 1742-RP)[J]. Science and Technology for the Built Environment, 2018, 24(1/2/3/4/5): 259. DOI:10.1080/23744731.2017.1365765 |
| [7] |
Korea Energy Ecomomics Institute. Energy consumption survey[M]. Sejong City: Ministry of Commerce, Industry and Energy(MOTIE), 2014.
|
| [8] |
American Society of Heating, Refrigerating and Air Conditioning Engineers Inc. ASHRAE handbook of fundamentals[R]. [S.l.]: Publication Traffic Administrator, 2017
|
| [9] |
石凯波, 王景刚, 鲍玲玲, 等. 基于邯郸商场人员密度及空调负荷特性研究[J]. 河北工程大学学报(自然科学版), 2017, 34(3): 74. SHI Kaibo, WANG Jinggang, BAO Linging, et al. Research on personnel density and air conditioning load characteristic in Handan shopping mall[J]. Journal of Hebei University of Engineering (Natural Science Edition), 2017, 34(3): 74. DOI:10.3969/j.issn.1673-9469.2017.03.016 |
| [10] |
丁研, 王朝霞, 朱能, 等. 办公建筑内部负荷扰量特性与计算方法[J]. 土木与环境工程学报(中英文), 2019, 41(4): 174. DING Yan, WANG Chaoxia, ZHU Neng, et al. Calculation method and characteristics of interior load disturbances for office buildings[J]. Journal of Civil and Environmental Engineering, 2019, 41(4): 174. DOI:10.11835/j.issn.2096-6717.2019.086 |
| [11] |
SPITLER J D, FISHER D E. On the relationship between the radiant time series and transfer function methods for design cooling load calculations[J]. HVAC&R Research, 1999, 5(2): 123. DOI:10.1080/10789669.1999.10391228 |
| [12] |
HOSNI M H, JONES B W, XU H. Experimental results for heat gain and radiant/convective split from equipment in buildings[J]. ASHRAE Transactions, 1999, 105: 527. |
| [13] |
LI R, ZHANG J. Real-time heat dissipation model of electronic equipment for determining the dynamic cooling demand of office buildings[J]. Journal of Building Engineering, 2022, 45: 103465. DOI:10.1016/J.JOBE.2021.103465 |
| [14] |
朱颖心. 建筑环境学[M]. 北京: 中国建筑工业出版社, 2010. ZHU Yingxin. Building environment[M]. Beijing: China Architecture & Building Press, 2010. |
| [15] |
章熙民, 任泽霈, 梅飞鸣. 传热学[M]. 5版. 北京: 中国建筑工业出版社, 2007. ZHANG Ximin, REN Zelin, MEI Feiming. Heattransfer[M]. 5th ed. Beijing: China Architecture & Building Press, 2007. |
| [16] |
卢玉峰, 刘西民. 复变函数[M]. 北京: 高等教育出版社, 2007. LU Yufeng, LIU Ximin. Complex function[M]. Beijing: Higher Education Press, 2007. |
| [17] |
刘思琦. 供暖系统中建筑(群)热力模型的辨识研究[D]. 哈尔滨: 哈尔滨工业大学, 2020 LIU Siqi. Identification of building(group) thermal model in heating system[D]. Harbin: Harbin Institute of Technology, 2020. DOI: 10.27061/d.cnki.ghgdu.2020.001550 |
| [18] |
LI Han, HU Haiiyu, KONG X, et al. Experimental study on human multi-node thermal sensitivity and thermal demand oriented to uniform environment[J]. Building and Environment, 2023(9): 243. DOI:10.1016/J.BUILDENV2023.110677 |
| [19] |
侯风. 集成球形相变颗粒的水泥基相变储能复合材料控温机理研究[D]. 郑州: 河南工业大学, 2023 HOU Feng. Study on temperature control mechanism of cementitious composites integrated with spherical phase change particles[D]. Zhengzhou: Henan University of Technology, 2023. DOI: 10.27791/d.cnki.ghegy.2023.000008 |
| [20] |
LI Ruonan, ZHANG Jili. A transfer function model of lighting heat dissipation for detecting time-delay effect and dynamic cooling demand during the real-time operation of buildings[J]. Energy and Buildings, 2022, 254: 111538. DOI:10.1016/j.enbuild.2021.111538 |
| [21] |
金忆丹, 尹永成. 复变函数与拉普拉斯变换[M]. 杭州: 浙江大学出版社, 2003. JIN Yidan, YIN Yongcheng. Complex function and Laplace transform[M]. Hangzhou: Zhejiang University Press, 2003. |
| [22] |
《环境科学大辞典》编委会. 环境科学大辞典[M]. 北京: 中国环境科学出版社, 2008. Editorial Committee of "Environmental Science Dictionary". Environmental science dictionary[M]. Beijing: China Environmental Press, 2008. |
| [23] |
秦臻. 传热学理论及应用研究[M]. 北京: 中国水利水电出版社, 2015. QIN Zhen. Heat transfer theory and application research[M]. Beijing: China Water & Power Press, 2015. |
| [24] |
赵亮. 建筑能源系统物联网数据监测与传输质量保障方法[D]. 大连: 大连理工大学, 2014 ZHAO Liang. Data quality guarantee in monitoring and transmission process of internet of building energy systems[D]. Dalian: Dalian University of Technology, 2014 |
 2024, Vol. 56
2024, Vol. 56



