2. 中国人民解放军93642部队, 河北 唐山 063000;
3. 中国人民解放军94636部队, 浙江 湖州 313112;
4. 空军工程大学 航空工程学院, 西安 710038
2. Unit 93642 of Chinese People's Liberation Army, Tangshan 063000, Hebei, China;
3. Unit 94636 of Chinese People's Liberation Army, Huzhou 313112, Zhejiang, China;
4. College of Aeronautics, Air Force Engineering University, Xi'an 710038, China
随着人工智能的发展,无人作战飞机(unmanned combat aircraft vehicle, UCAV)在现代战场中的作用及地位日益凸显。无人机感知技术作为UCAV自主空战的关键技术,为空战态势评估与决策提供一定的情报。无人机感知技术包括目标机机动识别以及轨迹预测。目标机轨迹识别为目标机轨迹预测提供历史轨迹与当前轨迹的战术特征信息。在高动态的空战对抗中,对目标机的机动动作进行快速、准确地识别不仅仅对预测目标机的战术机动意图具有重要意义,更是我机空战态势感知、威胁评估和战术机动决策的前提[1-2]。
空战目标机动识别问题实质上是一种多元时间序列模式识别问题,涉及特征选择、机动单元选取、机动分割点检测、相似性度量[3]、分类器设计等多个问题。国内外飞机机动识别文献相对较少,研究的方法包括模板匹配[4-6]、专家系统[7]、贝叶斯网络[8]、支持向量机[1-2]以及深度学习等[9-12]。模板匹配的机动识别方法不适合在线实时机动识别场景。基于专家系统的机动识别[7]没有考虑到飞机机动复杂多变、随机性强的特点。文献[8]根据专家知识,利用动态贝叶斯网络,解决机动模式分类问题,该方法主观性较强。文献[1]将复杂的飞行机动分解为多个可以理解的机动动作元,采用支持向量机(support vector machine, SVM)去解决飞机机动识别,该方法未考虑到机动时序性。文献[2]采用SVM的方法将复杂机动识别为5种简单的机动,不能够精准地反映机动模式。文献[13]提出了一种基于智能优化算法优化支持向量机的机动轨迹识别方法,试验结果表明该方法具有更高的精度,但是仍然需要耗费大量的训练时间。基于支持向量机的机动识别方法没有考虑到飞机机动的时序性,不能深度挖掘机动轨迹特征。文献[14]结合全卷积神经网络和双向长短期记忆网络对机动单元窗口的机动进行识别,实现了高效、实时识别,但是没有考虑到变量之间的关系。文献[15]针对空中目标样本数据知识匮乏等问题,提出了一种数据与知识双驱动的方法,但是缺乏对轨迹片段时间序列的建模与分析。文献[16]利用多项式方程对轨迹去拟合,得到拟合方程参数,以参数为训练样本去构建轨迹识别模型,该方法没有考虑动态性。文献[17]利用多策略差分进化算法改进动态时间规整方法,并将此方法应用到无人机飞行机动识别模型中,该方法虽然识别率较多,但是识别时间较长。基于深度学习的机动轨迹识别方法可以通过不同类型方法提取轨迹特征,训练构建基于神经网络的机动轨迹识别模型,但是仍然没有考虑到动态性,同时轨迹片段划分比较简单固化,不能泛化地表示各机动。
机动动作分割是复杂机动识别的前提,机动动作分割降低了复杂机动在线识别的复杂度。当前机动分割文献相对较少,机动分割方法主要包括基于特征点分割[18]、基于有监督学习分割点识别[19]、基于无监督分割点检测[20]。文献[18]根据趋势特征,将长时域飞行参数划分为单趋势序列,但是该类方法很容易受到噪声的干扰。文献[19]提出了一种基于分层SVM的异常点检测方法。文献[20]通过序聚类方法将分割问题转换为最优化问题,这类方法耗时比较长。基于有监督学习的分割点检测方法在识别较快、准确度较高,但是需要完备的数据与适当的特征空间。
上述方法虽然可以识别轨迹机动,但是存在以下问题:1)当前机动识别都是等长度识别,不能准确判断机动划分,没有统一的基本机动标准,导致识别方法不够泛化;2)当前机动识别没有考虑到时间序列的动态性;3)当前机动识别计算效率低,实时性较差[17]。深度学习作为一种先进的机器学习方法,广泛地应用于动作识别、语义分割等时间序列问题中,该方法能够深层次提取时间序列特征,且识别精度高,但是缺乏对不等长时间序列识别的应用。动态时间规整是一种基于形状的相似性度量方法,该方法能考虑到时序全局信息,且广泛应用于飞行机动识别问题中,但是动态时间规整的识别时间较长,不能应用于在线机动识别问题中,因此,为提高机动识别的实时性,将深度学习与动态时间规整结合去解决在线机动识别问题是一种新的思路。
针对当前机动动作识别方法存在上述问题,本文提出了一种基于马氏距离度量动态时间规整神经网络的在线飞机机动轨迹识别方法。首先,将基于机载测量飞行轨迹参数的在线机动动作识别问题分析等效为在线分割点检测和时间序列识别的融合问题;其次,分析轨迹特征,提取轨迹特征参数,分解机动动作,设计新的机动轨迹单元;然后,提出一种基于马氏距离支持向量机的机动轨迹分割点检测方法;最后,针对分割后的机动时间序列识别问题,提出了一种基于马氏距离动态时间规整神经网络的在线多元时间序列识别方法。仿真结果验证了该融合方法的可行性与实时性。
1 在线飞机机动轨迹识别问题分析作为一个在线多维时间序列分割识别问题,在线飞机机动轨迹识别问题主要包括目标轨迹特征提取、机动轨迹单元分解、分割点检测、时间序列分类识别等问题。在线飞机机动轨迹识别通过提取目标轨迹特征,利用分割点检测算法检测机动轨迹单元分割点,并对分割后的机动轨迹单元进行识别。具体的识别方案见图 1。
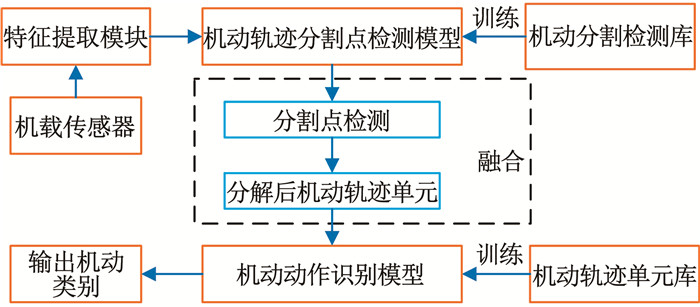
|
图 1 在线机动轨迹识别方案 Fig. 1 Online maneuvering trajectory recognition scheme |
假设UCAV机载传感器获取目标机机动轨迹坐标参数Pe, t=[xe, t, ye, t, ze, t],其中xe, t、ye, t与ze, t分别为目标机t时刻东向位置、北向位置与真实高度。经过特征提取模块,将目标机机动轨迹飞行坐标转化为机动轨迹特征参数;在分割点检测模块,先用机动分割检测库的样本训练机动轨迹分割模型,然后对实时输入的机动轨迹特征参数进行二分类,查找分割点;在机动识别模块,先用机动轨迹单元库的样本训练机动动作识别模型,然后对分割后的机动轨迹特征参数进行分类识别,得到相应的机动类型。
2 机动轨迹特征分析为更好解决在线机动轨迹识别问题,需要分析输入的轨迹信息以及输出的识别内容。本文分别从机动轨迹识别输入和输出的角度去分析问题。
2.1 机动轨迹特征获取为防止训练的分割点检测器与机动分类器过拟合,将机载传感器获得的轨迹参数转换成对检测与分类有用的特征。根据轨迹特征,本文选取了速率ve, t、航迹偏转角变化率Δψe, t、倾斜角变化率Δθe, t、高度变化率ΔHe, t、速率变化率Δve, t、累积航迹偏转角ψe, t、累积航迹倾斜角θe, t等特征[1-2]。假设目标机t-1时刻与t时刻的位置坐标为Pe, t-1=[xe, t-1, ye, t-1, ze, t-1]和Pe, t=[xe, t, ye, t, ze, t],两个连续时刻的时间差值为Δt,则当前时刻的速率可以定义如下:
| $ v_{\mathrm{e}, t}=\left|\boldsymbol{P}_{\mathrm{e}, t}-\boldsymbol{P}_{\mathrm{e}, t-1}\right| / \Delta t $ | (1) |
式中ve, t为目标机t时刻的速率,该特征可以体现目标机的速率状态信息。为体现目标机加速、减速、匀速等信息,定义速度变化率为
| $ \Delta v_{\mathrm{e}, t}=\left(v_{\mathrm{e}, t}-v_{\mathrm{e}, t-1}\right) / \Delta t $ | (2) |
在水平面内,机动轨迹单元明显可以分为左转弯、右转弯、直飞,主要是由航迹偏转角辨识。航迹偏转角变化率定义为目标瞬时运动方向在地面投影与正东方向的夹角为
| $ \Delta \psi_{\mathrm{e}, t}= \begin{cases}\arctan \left(\left(x_{\mathrm{e}, t}-x_{\mathrm{e}, t-1}\right) /\left(y_{\mathrm{e}, t}-y_{\mathrm{e}, t-1}\right)\right), & x_{\mathrm{e}, t}-x_{\mathrm{e}, t-1} \geqslant 0 \\ {\rm{ \mathsf{ π} }}+\arctan \left(\left(x_{\mathrm{e}, t}-x_{\mathrm{e}, t-1}\right) /\left(y_{\mathrm{e}, t}-y_{\mathrm{e}, t-1}\right)\right), & x_{\mathrm{e}, t}-x_{\mathrm{e}, t-1} <0, y_{\mathrm{e}, t}-y_{\mathrm{e}, t-1} \geqslant 0 \\ -{\rm{ \mathsf{ π} }}-\arctan \left(\left(x_{\mathrm{e}, t}-x_{\mathrm{e}, t-1}\right) /\left(y_{\mathrm{e}, t}-y_{\mathrm{e}, t-1}\right)\right), & x_{\mathrm{e}, t}-x_{\mathrm{e}, t-1} <0, y_{\mathrm{e}, t}-y_{\mathrm{e}, t-1} <0\end{cases} $ | (3) |
式中Δψe, t为左转为正,右转为负。为寻找分割点,累积航迹偏转角ψe, t从某一时刻开始直到角度加大到分割点处,重新开始累加角度。例如,左转累加到90°、180°分别为分割点处,这样处理主要是缩短待识别轨迹的长度。累积航迹偏转角ψe, t可表示为
| $ \psi_{\mathrm{e}, t}=\sum\limits_t \Delta \psi_{\mathrm{e}, t} $ | (4) |
在垂直平面内,机动轨迹单元可以分为爬升、俯冲、水平直飞,主要是由高度变化率、倾斜角表示。倾斜角变化率是指目标机瞬时运动方向与水平面的夹角,其定义如下:
| $ \Delta \theta_{\mathrm{e}, t}=\arctan \left(\Delta H_{\mathrm{e}, t} / \sqrt{\left(x_{\mathrm{e}, t}-x_{\mathrm{e}, t-1}\right)^2+\left(y_{\mathrm{e}, t}-y_{\mathrm{e}, t-1}\right)^2}\right) $ | (5) |
式中,ΔHe, t为高度变化率,ΔHe, t=(ze, t-ze, t-1)/Δt。ΔHe, t与Δθe, t上升为正,下降为负。累积倾斜角θe, t达到90°,会可能突变为-90°,所以要重新累加倾斜角。累积倾斜角θe, t可表示为
| $ \theta_{\mathrm{e}, t}=\sum\limits_t \Delta \theta_{\mathrm{e}, t} $ | (6) |
目标机的轨迹预测不仅仅需要预测下一时刻的轨迹点,还要预测目标机的下一个战术机动轨迹。从战术角度来看,研究机动轨迹单元是识别与预测目标机动轨迹的关键与前提。为了快速直观地学习机动轨迹单元,空战机动可以分为水平面机动动作、垂直面机动动作和空间组合机动[1]。
在水平面内,根据航迹偏转角,机动动作可以分为平飞、左转弯和右转弯。水平面内的机动轨迹单元分为3种模式,如图 2中所示的E01, E08和E15。
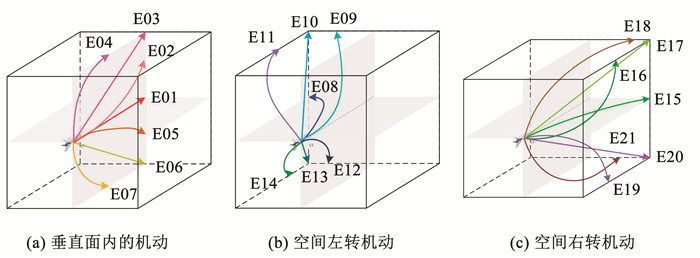
|
图 2 机动轨迹单元示意 Fig. 2 Schematic diagram of maneuver trajectory units |
在垂直面内,根据倾斜角、高度变化率,机动动作可以分为爬升与俯冲。本文采用航迹倾斜角变化率来区分垂直面内的轨迹形状。同时,利用累积倾斜角来区分爬升与俯冲。大多数文献将直线上飞与下降轨迹单元分为凹上爬升与凸下飞这两种机动轨迹单元类别[1],在本文中,尽管直上飞与直下降轨迹在空战中较少使用,但是进行这两种轨迹机动为了更快地优势占位,减少对方对自己的威胁,具有战术意义,同时可以完备识别空间,因此,考虑将直上飞与直下降轨迹单元设为基本单元。垂直面内的机动轨迹单元分为6种模式:(凹上爬升、直上飞、凸上爬升、凸下俯冲、直下飞、凹下俯冲),如图 2(a)中所示的E02-E07。
在空间中,可以将一个空间动作分解为水平面内机动与垂直面内机动。按照水平面内的分类,将空间机动轨迹单元分为两大类:空间左转弯机动与空间右转弯机动;再按照垂直面内的分类,将空间左转弯机动分为左转弯凹上飞、左转弯直上飞、左转弯凸上飞、左转弯凸下飞、左转弯直下飞以及左转弯凹下飞,空间右转弯类似于空间左转弯。空间左转机动轨迹单元具体分类如图 2(b)中所示的E09-E14。与左转弯类似,空间右转机动轨迹单元具体分为右转弯凹上飞、右转弯直上飞、右转弯凸上飞、右转弯凸下飞、右转弯直下飞以及右转弯凹下飞(除了水平右转弯),空间右转机动轨迹单元具体分类如图 2(c)中所示的E16-E21。
3 基于马氏距离支持向量机的机动分割点检测模型 3.1 机动分割点检测模型机动分割点检测主要是将一个长时域的飞机机动轨迹按照一定的规则进行分割,为机动轨迹单元识别提供可靠的飞行参数识别时间序列。假设机载传感器实时地提供目标机飞行轨迹参数,并且能够及时地计算获得特征参数,记起始时刻为t0,当前时刻为tcurrent,该时间段提取的特征为Xe, t=[ψe, t, Δψe, t, θe, t, Δθe, t, ΔHe, t, ve, t, Δve, t],其中t∈[t0, tcurrent]。根据分割点检测技术,可以得到分割点集S={Xe, s|Ye, s=1},其中: Ye, s为分割点标签,Ye, s=1表示该点为分割点,否则为机动轨迹单元内点(非分割点); 下标s为分割点索引,表示为第s个分割点的时间点索引。根据空战训练数据提取的特征参数,可以通过有监督学习的方法去训练机动分割点检测模型,然后搭载到UCAV,在线完成机动分割点的识别。
3.2 基于马氏距离度量的支持向量机机动轨迹分割检测库训练数据是不平衡数据[21],分割点的样本数据少于非分割点样本数据。数据库中存在少量的噪声干扰数据[22],例如飞机失速的轨迹样本点。分割检测特征参数需要相邻两个时刻的机动轨迹样本点数据,则训练数据为非线性分布数据。本文要解决的分割点检测问题是一个二分类问题。根据机动分割点检测问题的特征,本文采用基于高斯核函数的支持向量机。考虑到各种特性之间的相关性,本文引入马氏距离(Mahalanobis distance)到高斯核函数中。SVM结合马氏距离,提出了一种基于马氏距离支持向量机(Mahalanobis distance-based SVM, MDSVM)的度量学习方法。
假设机动轨迹分割点样本集为Ps={(Xe, i, Ye, i)|Xe, i=Xe, t, Ye, i=±1, i=1, …, p},其中p为样本个数。每一个训练样本Xe对应一个类别标签Ye=±1,分别表示两类的类别标签。设Xe为N维输入空间的向量,ϕ(Xe)为Xe通过非线性变换之后的特征向量,对应的划分超平面模型为
| $ f\left(\boldsymbol{X}_{\mathrm{e}}\right)=\boldsymbol{w}^{\mathrm{T}} {\phi}\left(\boldsymbol{X}_{\mathrm{e}}\right)+b $ | (7) |
为解决样本点落在超平面与边界之间的问题,引入松弛变量,则目标函数为:
| $ \begin{aligned} & \min\limits_{w, b}\left(\frac{1}{2}\|\boldsymbol{w}\|^2+C \sum\limits_{i=1}^p \xi_i\right) \\ & \text { s.t. } Y_{\mathrm{e}, i}\left(\boldsymbol{w}^{\mathrm{T}} {\phi}\left(\boldsymbol{X}_{\mathrm{e}, i}\right)+b\right) \geqslant 1-\xi_i(i=1, \cdots, p) \end{aligned} $ | (8) |
式中:ξi≥0为松弛变量,C>0为惩罚参数,C可以调和式(8)中两项的影响程度。
结合马氏距离与高斯核函数,提出基于马氏距离的高斯核函数:
| $ \begin{aligned} \kappa\left(\boldsymbol{X}_{\mathrm{e}, i}, \boldsymbol{X}_{\mathrm{e}, j}\right)= & \exp \left(-\gamma\left(\boldsymbol{X}_{\mathrm{e}, i}-\boldsymbol{X}_{\mathrm{e}, j}\right)^{\mathrm{T}} \boldsymbol{M}\left(\boldsymbol{X}_{\mathrm{e}, i}-\boldsymbol{X}_{\mathrm{e}, j}\right)\right)= \\ & \exp \left(-\gamma\left\|\boldsymbol{A}^{\mathrm{T}} \boldsymbol{X}_{\mathrm{e}, i}-\boldsymbol{A}^{\mathrm{T}} \boldsymbol{X}_{\mathrm{e}, j}\right\|^2\right) \end{aligned} $ | (9) |
式中:(Xe, i-Xe, j)TM(Xe, i-Xe, j)为数据点Xe, i与Xe, j之间的马氏距离的平方,M为马氏矩阵,是一个半正定矩阵;A为投射矩阵,将原始特征投影到新的特征空间,消除不同维度之间的相关性,同时分配不同的权重给不同的特征,其满足 M=AAT;γ为自由参数,主要用来控制高斯核函数的分布情况。
为求解目标函数(8),将其转化为拉格朗日函数:
| $ \begin{gathered} L\left(\boldsymbol{w}, b, \phi_{\boldsymbol{M}}, \xi, \alpha, r\right)=\frac{1}{2}\|\boldsymbol{w}\|^2+C \sum\limits_{i=1}^p \xi_i- \\ \sum\limits_{i=1}^p \alpha_i\left(Y_{\mathrm{e}, i}\left(\boldsymbol{w}^{\mathrm{T}} \phi_{\boldsymbol{M}}\left(\boldsymbol{X}_{\mathrm{e}, i}\right)+b\right)-1+\xi_i\right)-\sum\limits_{i=1}^p r_i \xi_i \end{gathered} $ | (10) |
式中: αi、ri分别为拉格朗日参数,满足αi>0和ri>0;转换函数ϕM包括投射矩阵A与自由参数γ,一般情况下,自由参数是初始化设定好的。拉格朗日函数(10)需要优化的变量从(w, b, ϕM, ξ, α, r)变为(w, b, A, ξ, α, r),则式(8)的优化目标变为
| $ \min\limits_{\boldsymbol{w}, b, \boldsymbol{A}, \xi} \max\limits_{\alpha, r} L(\boldsymbol{w}, b, \boldsymbol{A}, \xi, \alpha, r) $ | (11) |
式(11)的优化主要思路为:
1) 朗格朗日函数对法向量 w、偏置量b和拉格朗日参数ξ进行求偏导,得到简化的拉格朗日函数:
| $ \begin{aligned} \min\limits_A \max _{0 \leqslant \alpha_i \leq C, b} L= & \sum\limits_{i=1}^p \alpha_i-b \sum\limits_{i=1}^p \alpha_i Y_{\mathrm{e}, i}- \\ & \frac{1}{2} \sum\limits_{i, j=1}^p \alpha_i \alpha_j Y_{\mathrm{e}, i} Y_{\mathrm{e}, j} \kappa\left(\boldsymbol{X}_{\mathrm{e}, i}, \boldsymbol{X}_{\mathrm{e}, j}\right) \end{aligned} $ | (12) |
2) 固定投射矩阵A,分别对α和b求偏导,其更新公式如下:
| $ \frac{\partial L}{\partial \alpha_i}=1-\sum\limits_{j=1} \alpha_j-Y_{\mathrm{e}, i} b \begin{cases}\leqslant 0, & \alpha_i=0 \\ =0, & 0 <\alpha_i <C \\ \leqslant 0, & \alpha_i=C\end{cases} $ | (13) |
| $ \frac{\partial L}{\partial b}=-\sum\limits_{i=1} \alpha_i Y_{\mathrm{e}, i}=0 $ | (14) |
式中,利用序列最小优化算法(sequential minimal optimization, SMO)[23]求解该优化问题。
3) 固定SVM的朗格朗日参数α和偏置量b,更新马氏距离的固定投射矩阵A。在本算法中,固定α和b,以式(12)的第3项为优化函数,采用梯度下降法更新A:
| $ \boldsymbol{A}_*=\boldsymbol{A}_t-\tau_t \frac{\partial L}{\partial \boldsymbol{A}_t} $ | (15) |
| $ \frac{\partial L}{\partial \boldsymbol{A}_t}=\sum\limits_{i, j=1}^p \gamma \alpha_i \alpha_j Y_{\mathrm{e}, i} Y_{\mathrm{e}, j} \boldsymbol{v}_{i, j} \boldsymbol{v}_{i, j}^{\mathrm{T}} \boldsymbol{A}_t \exp \left(-\gamma \boldsymbol{v}_{i, j}^{\mathrm{T}} \boldsymbol{A}_t \boldsymbol{A}_t^{\mathrm{T}} \boldsymbol{v}_{i, j}\right) $ | (16) |
式中: vi, j=Xe, i-Xe, j。如果L(A*) < L(At),则At+1=A*和τt+1=τ0;否则,At+1=At和τt+1=τt/2。基于马氏距离度量的支持向量机伪代码见算法1。算法1的优化投射矩阵A、朗格朗日参数α和偏置量b的方式可以提高基于MDSVM的度量学习算法运行效率。由于优化投射矩阵A的方式与优化朗格朗日参数α和偏置量b的方式不同,同时优化A、α和b的方式使得优化维度增加,导致基于MDSVM的度量学习算法运行时间增加,从而降低了学习效率。
算法1 基于MDSVM的度量学习算法
1. 输入样本Xe与样本标签Ye;
2. 设置参数: 外层SVM参数优化迭代次数loop, 内层马氏距离优化迭代次数iter, 其他参数τ0和γ;
3. 初始化投射矩阵A0=I;
4. for l=1:loop do
5. 根据式(9),构建基于马氏距离的高斯核函数;
6. 利用SMO算法优化L,得到SVM参数α和b;
7. 设置At=A0和τt=τ0;
8. for t=1:iter do
9. 根据式(10),计算A*;
10. 通过判断A*和At的目标函数值,更新步长与投射矩阵;
11. end
12. end
13. 输出马氏矩阵M;
14. 利用M和SMO算法求得SVM参数.
根据上述分析,采用基于马氏距离度量的支持向量机算法去构建机动分割点检测模型。机动分割点检测步骤如下:
Step1 利用机动数据库中产生机动分割检测库,提取相关特征参数Xe,构建数据集Ps。将数据集分为训练集、验证集、测试集,利用训练集离线训练MDSVM,得到分割点检测模型。
Step2 通过机载传感器接受到特征参数Xe, t后,传入在线分割点检测模型中,判断当前轨迹点是否为分割点。
4 基于马氏距离动态时间规整神经网络的机动识别模型 4.1 机动轨迹识别模型机动轨迹识别问题是一个多维时间序列识别问题。机动轨迹识别将轨迹分割后的机动轨迹单元特征参数Xe=[ψe, Δψe, θe, Δθe, ΔHe, ve, Δve]为输入,以机动轨迹单元类别为输出,为预测目标机状态与态势评估提供关键信息。本文采用有监督学习的方法训练机动轨迹识别模型。根据空战训练数据提取的特征参数,可以通过有监督学习的方法去训练机动轨迹识别模型,然后搭载到UCAV,在线完成机动轨迹单元的识别。
4.2 基于马氏距离度量的动态时间规整神经网络多维时间序列分类识别是在线机动识别研究的核心技术,本文采用的核心方法是基于马氏距离的DTW(Mahalanobis distance-based dynamic time warping, MDDTW)与卷积神经网络(convolutional neural network, CNN) [24-25]。本文结合MDDTW与CNN,提出一种新的时间序列识别神经网络,即MDDTWnet。
4.2.1 基于动态三元约束策略的马氏距离度量方法为适应训练样本数据的增加,本文采用了基于动态三元约束策略的马氏距离度量(dynamic triplet strategy based Mahalanobis distance, DTSMD)方法[26]。DTSMD学习方法是一个在线度量学习方法,相较于传统离线度量学习算法,其可以在某一时刻接受不同的样本,而且期望马氏矩阵可以根据目标函数进行更新,得到最优的马氏矩阵。
DTSMD模型[26]如下:
| $ \boldsymbol{M}_{t+1}=\underset{\boldsymbol{M} \geqslant 0}{\operatorname{argmin}} D_{\mathrm{ld}}\left(\boldsymbol{M}, \boldsymbol{M}_t\right)+\eta_t L\left(\boldsymbol{M}, y_t^{\prime}, y_t\right) $ | (17) |
式中:Mt为迭代次数为t的马氏矩阵, ηt>0为正则化参数,主要平衡正则化函数Dld(M, Mt)与损失函数L(M, y′t, yt);y′t、yt分别为约束中的预测值与目标值,y′t、yt主要是由构建的训练约束决定的。目前,最常用的学习约束包括标记约束、对约束、三元约束{Xe, i, Xe, j, Xe, k}。相对于其他约束,三元约束是最弱的约束,可以训练出普遍适应的马氏矩阵M。
目标函数(17)对M求导,其中Dld(M, Mt)梯度为Mt-1-M-1,ηtL(M, y′t, yt)的梯度为:
| $ \frac{\mathrm{d}}{\mathrm{~d} \boldsymbol{M}}\left({\eta}_t L(\boldsymbol{M})\right)= \begin{cases}0, & \left(\boldsymbol{q}_t^{\mathrm{T}} \boldsymbol{M}_t \boldsymbol{q}_t-\boldsymbol{p}_t^{\mathrm{T}} \boldsymbol{M}_t \boldsymbol{p}_t\right) \geqslant \rho \\ {\eta}_t\left(\boldsymbol{p}_t \boldsymbol{p}_t^{\mathrm{T}}-\boldsymbol{q}_t \boldsymbol{q}_t^{\mathrm{T}}\right), & \left(\boldsymbol{q}_t^{\mathrm{T}} \boldsymbol{M}_t \boldsymbol{q}_t-\boldsymbol{p}_t^{\mathrm{T}} \boldsymbol{M}_t \boldsymbol{p}_t\right)<\rho\end{cases} $ | (18) |
式中:pt=Xe, i-Xe, j,qt=Xe, i-Xe, k。如果(qtTMtqt-ptTMtpt) < ρ,则
| $ \boldsymbol{M}_{t+1}=\left(\boldsymbol{M}_t^{-1}+\eta_t\left(\boldsymbol{p}_t \boldsymbol{p}_t^{\mathrm{T}}-\boldsymbol{q}_t \boldsymbol{q}_t^{\mathrm{T}}\right)\right)^{-1} $ | (19) |
为解决式(19)的计算,采用Sherman-Morrison公式为
| $ \left(\boldsymbol{A}+u \boldsymbol{v}^{\mathrm{T}}\right)^{-1}=\boldsymbol{A}^{-1}-\frac{\boldsymbol{A}^{-1} u \boldsymbol{v}^{\mathrm{T}} \boldsymbol{A}^{-1}}{1+\boldsymbol{v}^{\mathrm{T}} \boldsymbol{A}^{-1} u} $ | (20) |
根据式(20),假设γt=(Mt-1+ηtptptT)-1,则Mt+1=(γt-1-ηtqtqtT)-1。利用式(19),则Mt+1更新公式为:
| $ \gamma_t=\boldsymbol{M}_t-\frac{\eta_t \boldsymbol{M}_t \boldsymbol{p}_t \boldsymbol{p}_t^{\mathrm{T}} \boldsymbol{M}_t}{1+\eta_t \boldsymbol{p}_t^{\mathrm{T}} \boldsymbol{M}_t \boldsymbol{p}_t} $ | (21) |
| $ \boldsymbol{M}_{t+1}=\gamma_t+\frac{\eta_t \gamma_t \boldsymbol{q}_t \boldsymbol{q}_t^{\mathrm{T}} \gamma_t}{1+\eta_t \boldsymbol{q}_t^{\mathrm{T}} \gamma_t \boldsymbol{q}_t} $ | (22) |
正则化参数ηt平衡正则化函数与损失函数的权重,过大的ηt,则偏重于损失函数,过小的ηt,则度量学习比较慢。因此,本文选择一个自适应的正则化参数:
| $ \eta_t=\frac{\alpha}{\operatorname{tr}\left(\left(\boldsymbol{I}-\boldsymbol{M}_t\right)^{-1} \boldsymbol{M}_t \boldsymbol{q}_t \boldsymbol{q}_t^{\mathrm{T}}\right)} $ | (23) |
为克服度量学习中使用全部的三元约束带来的计算负担,本文采用了一种动态三元约束策略,具体策略详见文献[25]。
4.2.2 基于马氏距离度量的动态时间规整为了将DTW扩展到多维时间序列相似性度量中,本文采用DTSMD进行时间序列的局部度量。设3个多维时间序列样本Xe=[xe(1), …, xe(tx)],Ye=[ye(1), …, ye(ty)],Ze=[ze(1), …, ze(tz)],其中 Xe∈Rd×tx,xe(i)∈Rd,Ye∈Rd×ty,ye(j)∈Rd,Ze∈Rd×tz,ze(k)∈Rd。局部距离度量定义如下:
| $ D\left(x_{\mathrm{e}}(i), y_{\mathrm{e}}(j)\right)=\sum\limits_{k=1}^d\left(x_{\mathrm{e}, k}(i), y_{\mathrm{e}, k}(j)\right)^2 $ | (24) |
根据式(24),基于马氏距离的局部度量为
| $ D_{\boldsymbol{M}}\left(x_{\mathrm{e}}(i), y_{\mathrm{e}}(j)\right)=\left(x_{\mathrm{e}}(i)-y_{\mathrm{e}}(j)\right)^{\mathrm{T}} \boldsymbol{M}\left(x_{\mathrm{e}}(i)-y_{\mathrm{e}}(j)\right) $ | (25) |
根据式(25),基于马氏距离的DTW算法为
| $ \operatorname{Dist}_{\boldsymbol{M}}(i, j)=D_{\boldsymbol{M}}\left(x_{\mathrm{e}}(i), y_{\mathrm{e}}(j)\right)+\min \left\{\begin{array}{l} \operatorname{Dist}_{\boldsymbol{M}}(i-1, j-1) \\ \operatorname{Dist}_{\boldsymbol{M}}(i-1, j) \\ \operatorname{Dist}_{\boldsymbol{M}}(i, j-1) \end{array}\right. $ | (26) |
根据最优规整路径,得到规整时间序列[xe(k), ye(k)]=[xe(ωx(k)), ye(ωy(k))],其中,ωx(k)与ωy(k)为规整路径。结合式(25),MDDTW计算如下:
| $ \begin{aligned} \operatorname{DTW}_{\boldsymbol{M}}\left(\boldsymbol{X}_{\mathrm{e}}, \boldsymbol{Y}_{\mathrm{e}}\right)= & \sum\limits_{k=1}^{\mathrm{p}}\left(\bar{x}_{\mathrm{e}}\left(\omega_x(k)\right)-\bar{y}_{\mathrm{e}}\left(\omega_y(k)\right)\right)^{\mathrm{T}} \cdot \\ & \boldsymbol{M}\bar{x}_{\mathrm{e}}\left(\omega_x(k)\right)-\bar{y}_{\mathrm{e}}\left(\omega_y(k)\right)= \\ & \operatorname{tr}\left(\boldsymbol{P}^{\mathrm{T}} \boldsymbol{M P}\right) \end{aligned} $ | (27) |
式中:Pd×p=Xe-Ye,d为特征向量维度,p为规整路径。
4.2.3 动态时间规整神经网络CNN处理不等长时间序列识别问题时,目前解决的方法主要分为两种:1)将时间序列的动态数据点看作静态数据点,但该方法受到噪声点的干扰;2)将不等长时间序列进行插入拟合,使不等长时间序列变为等长时间序列,但这种方法使原时间序列失真。针对CNN的卷积操作对时间序列的缺陷与不足,本文采用了一种基于动态权重对齐(dynamic weight alignment, DWA)策略的神经网络,具体结构见图 3。
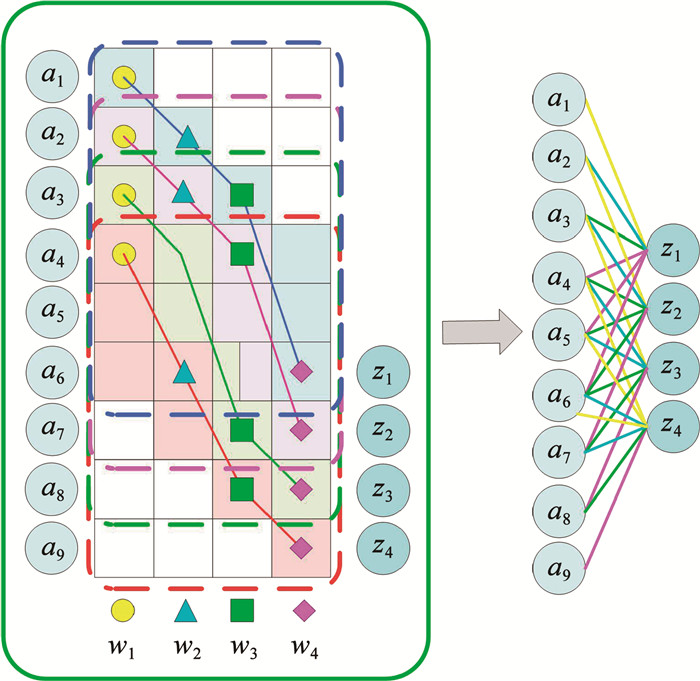
|
图 3 动态权重对齐策略 Fig. 3 Dynamic weight alignment strategy |
DWA策略的前向传播主要分为两步,具体步骤如下:
Step1 计算每个卷积核共享权重与感受视野窗口输入之间的DTW,先用动态规划方法计算累加代价矩阵,然后利用累加代价矩阵寻找DTW规整路径:
| $ \operatorname{Dist}(i, j)=D(a(i), w(j))+\min \left\{\begin{array}{l} \operatorname{Dist}(i-1, j-1) \\ \operatorname{Dist}(i-1, j) \\ \operatorname{Dist}(i, j-1) \end{array}\right. $ | (28) |
| $ \begin{aligned} \operatorname{DTW}_{\text {net }}(\boldsymbol{a}, \boldsymbol{w})= & \operatorname{Dist}\left(n_a, n_w\right)= \\ & \sum\limits_{k=1}^{\mathrm{p}} D\left(\bar{a}\left(\omega_a(k)\right), \bar{w}\left(\omega_w(k)\right)\right) \end{aligned} $ | (29) |
式中:Dist(i, j)为当前索引i与j之间的累加代价,D(x(i), w(j))为输入a(i)与卷积核权重w(j)之间的基于欧式距离局部度量,DTWnet(a, w)为输入与权重之间的DTW距离,na、nw分别为输入的时间长度与卷积核的宽度,ωa(k)、ωw(k)分别为输入与权重规整后的第k个索引,a、w分别为规整后的输入与权重,p为规整路径。
Step2 根据规整路径p、输入 a与共享权重 w,计算卷积之后的特征值:
| $ z_j^{(l)}=\sum\limits_{i=1}^{\mathrm{p}} \overline{\boldsymbol{w}}_i^{(l)} \overline{\boldsymbol{a}}_{i+j-1}^{(l-1)}+b^{(l)} $ | (30) |
利用规整路径去匹配输入与权重,然后让匹配规整后的路径进行卷积操作,这样就不用翻转激活函数。共享权重的对齐匹配随着卷积的每一步进行,且每一次迭代中仅仅保留当前的规整路径。
权重与偏置量的优化是损失函数误差通过反向传播实施的。权重与偏置量的优化算法采用的是Adam优化算法[26-27]。与传统神经网络层一样,根据链式传递规则,则基于DWA的卷积层相对权重的梯度计算如下:
| $ \begin{aligned} \boldsymbol{g}= & \sum\limits_i \frac{\partial L}{\partial z_j^{(l)}} \frac{\partial\left(\sum\limits_{i^{\prime}, j^{\prime} \in p} \bar{w}_{i^{\prime}}^{(l)} \bar{a}_{j^{\prime}}^{(l-1)}+b^{(l)}\right)}{\partial w_i^{(l)}}= \\ & \delta^{(l+1)} \sum\limits_{i^{\prime}, j^{\prime} \in p} \bar{a}_{j^{\prime}}^{(l-1)} \end{aligned} $ | (31) |
式中:L为损失函数,δ(l+1)为通过链式规则反向传播前一层的误差。为解决在深度神经网络初期降低梯度消失或者爆炸问题,利用批量归一化技术(batch normalization)[28]。
4.2.4 基于马氏距离的动态时间规整神经网络基于MDDTW度量学习算法与DTWnet时间序列识别网络,提出了一种基于马氏距离的动态时间规整神经网络(MDDTWnet),主要用来解决多维时间序列的识别分类问题。首先利用度量学习算法学习马氏距离,然后利用该马氏距离去度量卷积层输入与共享权重之间DTW距离,最后采用Adam优化算法对MDDTWnet进行训练优化。MDDTWnet伪代码见算法2。
算法2 MDDTWnet伪代码
1. 输入训练样本Xe和样本标签Ye;
//基于MDDTW的度量学习//
2. 初始化三元约束, 边际ρ, 学习速率α, 最大迭代次数iter;
3. 初始化马氏矩阵M0=I;
4. while loop < =max_loop do
5. 利用动态三元约束策略,更新三元约束集;
6. 利用MDDTW算法与式(26)得到路径规整W;
7. 根据约束条件与式(21)、(22),计算Mt+1;
8. loop=loop+1;
9. end
10. 得到最优马氏矩阵M;
//训练MDDTWnet神经网络 //
11. 初始化MDDTWnet相关参数;
12. 输入马氏矩阵;
13. while iter < =max_iter do
14. 利用MDDTW方法计算卷积核与输入之间的规整路径;
15. 依据规整路径去完成卷积核与该层输入之间的卷积操作;
16. 完成其余各层的前向计算;
17. 根据损失函数,计算与传递各层的误差;
18. 在反向传播中,根据Adam算法,利用误差更新神经网络的参数;
19. end
机动轨迹识别模块采用了基于马氏距离度量的动态时间规整神经网络,将分割后的机动轨迹单元进行识别,为预测目标机状态与态势评估提供关键信息。Xe=[ψe, Δψe, θe, Δθe, ΔHe, ve, Δve]为机动轨迹单元特征参数。机动轨迹识别步骤如下:
Step1 离线训练。利用空战数据,提取相关特征参数和机动轨迹单元库,通过基于MDDTW的度量学习算法,得到马氏矩阵 M7×7,其中,“7”为分类训练样本的维数;将马氏矩阵带入到MDDTWnet神经网络训练多维时间序列样本,得到MDDTWnet识别网络。
Step2 在线识别目标机动轨迹。在空战中,将分割后的机动轨迹输入到MDDTWnet识别网络,判断当前轨迹是属于哪个机动轨迹单元类别。
5 在线目标机动轨迹识别根据上述分析,基于MDSVM分割点检测与基于MDDTWnet分类的在线目标机机动识别融合(MDSVM-MDDTWnet)方法流程如图 4所示,具体的步骤如下:

|
图 4 在线目标机动轨迹识别流程 Fig. 4 Flow chart of online aircraft maneuver recognition |
Step1 利用空战训练测量仪(air combat maneuvering instrument, ACMI)[2]的空战数据,通过机动轨迹特征分析,建立机动分割检测库与机动轨迹单元库。
Step2 利用机动分割检测库通过基于MDSVM的度量学习算法获得分割样本库马氏矩阵Mseg。利用机动分割检测库训练集训练MDSVM机动轨迹分割器。
Step3 利用机动轨迹单元库通过MTSMD的度量学习算法获得机动轨迹单元样本库马氏矩阵MDTW。利用机动轨迹单元库训练集训练MDDTWnet机动轨迹单元分类识别器。
Step4 输入机载传感器获取的目标机机动轨迹参数,将特征提取后的参数输入到MDSVM在线分割点检测器中,输出分割后的机动轨迹参数。
Step5 将分割后的机动轨迹特征参数输入到MDDTWnet中,输出包含分割后的机动轨迹单元类别标签的识别结果。
6 仿真与分析DTW与神经网络结合方法是解决多维时间序列识别问题的新思路。为验证基于马氏距离度量的动态时间规整神经网络在飞机机动轨迹在线识别问题下的可行性与有效性,本文采用Matlab2018b仿真平台对文中提出的在线机动轨迹分割识别方法进行仿真。仿真环境为Windows 10系统,处理器为AMD Ryzen 9 5900HX with Radeon Graphics,内存为16.0 GB。
6.1 机动轨迹分割点检测仿真分割点检测库的样本数据来源于空战训练测量仪(air combat maneuvering instrument, ACMI)采集的空战训练轨迹数据,样本数量达到3 618 907,非分割点为3 457 661,分割点161 246,该数据集属于不平衡数据分布,这也符合机动轨迹单元占据大比例。为验证MDSVM算法在飞行机动分割点检测中的鲁棒性与有效性,该仿真试验每次随机提取总样本数的4%,其中:3%用来训练MDSVM,1%作为测试集来测试SVM的性能。同时,该仿真试验运行20次。
下式给出了分割检测训练样本的马氏矩阵Mseg。图 5给出了基于MDSVM的分割点样本检测混淆矩阵。从图 5可以看出,目标类别有-1和1,其中:-1为该样本点不是分割点,1为该样本点是分割点。非分割点测试样本数为1 725,分割点测试样本数为1 617,检测的结果为非分割点的样本数量为1 825,其中有100个点误分为分割点。总体上,MDSVM在分割点样本检测中准确率为97.0%。
| $ \boldsymbol{M}_{\mathrm{seg}}=\left[\begin{array}{rrrrrrrrrr} 2.510 & -2.250 & -1.960 & -1.550 & -0.050 & -0.100 & 0.050 & 0.050 & -0.060 & -0.010 \\ -2.250 & 2.060 & 1.910 & 1.510 & 0.010 & 0.070 & -0.050 & -0.050 & 0.070 & 0.070 \\ -1.960 & 1.910 & 2.310 & 1.540 & -0.070 & -0.001 & -0.070 & -0.080 & 0.150 & 0.150 \\ -1.550 & 1.510 & 1.540 & 1.520 & -0.060 & -0.001 & -0.060 & -0.060 & 0.100 & 0.100 \\ -0.050 & 0.010 & -0.070 & -0.060 & 0.180 & -0.120 & -0.004 & -0.002 & -0.050 & -0.050 \\ -0.100 & 0.070 & 0.001 & 0.001 & -0.120 & 0.170 & 0.010 & 0.010 & -0.050 & -0.050 \\ 0.050 & -0.050 & -0.070 & -0.060 & -0.004 & 0.010 & 0.300 & -0.020 & -0.008 & -0.006 \\ 0.050 & -0.050 & -0.080 & -0.060 & -0.002 & 0.010 & -0.020 & 0.290 & -0.010 & -0.010 \\ -0.020 & 0.070 & 0.150 & 0.100 & -0.050 & -0.050 & -0.008 & -0.010 & 0.340 & 0.030 \\ -0.010 & 0.070 & 0.150 & 0.100 & -0.050 & -0.050 & -0.006 & -0.010 & 0.030 & 0.340 \end{array}\right] $ | (32) |
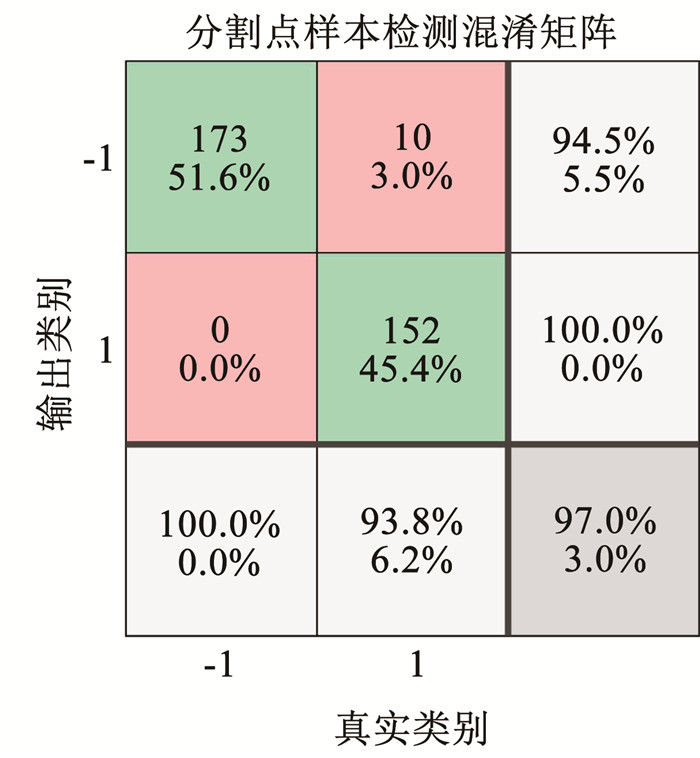
|
图 5 基于MDSVM的分割点样本检测混淆矩阵(1为分割点,-1为非分割点) Fig. 5 Confusion matrix for segmentation sample detection based on MDSVM(1 is split point, -1 is not split point) |
为验证本文提出的在线机动轨迹识别方法的有效性与鲁棒性,首先利用机动轨迹单元库去获取MDDTWnet的DTW核数量与核尺寸(DTW核的长度);其次利用机动轨迹单元库的训练与测试MDDTWnet神经网络性能。比较算法的参数设置详见表 1。机动轨迹单元库的样本数据主要来源于模拟飞机机动轨迹数据与真实空战训练轨迹数据,得到样本数量77 470,其中:垂直面内机动轨迹数量为19 808,空间左转机动轨迹数量为23 674,空间右转机动轨迹数量为33 988。每个仿真实验运行20次,统计20次的识别结果。
| 表 1 比较算法的参数设置 Tab. 1 Parameters setting of compared algorithms |
为找到合适的DTW核参数,本文分析了不同数量与不同尺寸的核对MDDTWnet神经网络的影响。在本仿真实验中,选取4 120个样本作为训练样本、1 050个样本作为测试样本。MDDTWnet结构与上述实验一样,本仿真实验中选取不同的DTW核数量与尺寸。不同DTW核对MDDTWnet的影响结果见图 6。由图 6可知,随着DTW核数量增加,识别精度增加,识别时间也增加;随着DTW核长度增加,识别精度增加,识别时间也增加。为增加MDDTWnet识别精度、减少识别时间,本文选取DTW核的数量为25,核长度比例为Skernel=0.9,因此,核长度为0.9倍机动轨迹单元时间序列长度。

|
图 6 不同1TW核数量对MDDTWnet的影响 Fig. 6 Impact of different DTW kernel on MDDTWnet |
根据上文MDDTWnet参数分析仿真实验,得到核数量为25,核长度为DTW核的尺寸为7(机动轨迹单元空间维度)×0.9倍时间序列长度(机动轨迹单元时间维度为15),其他MDDTWnet参数设置同上。
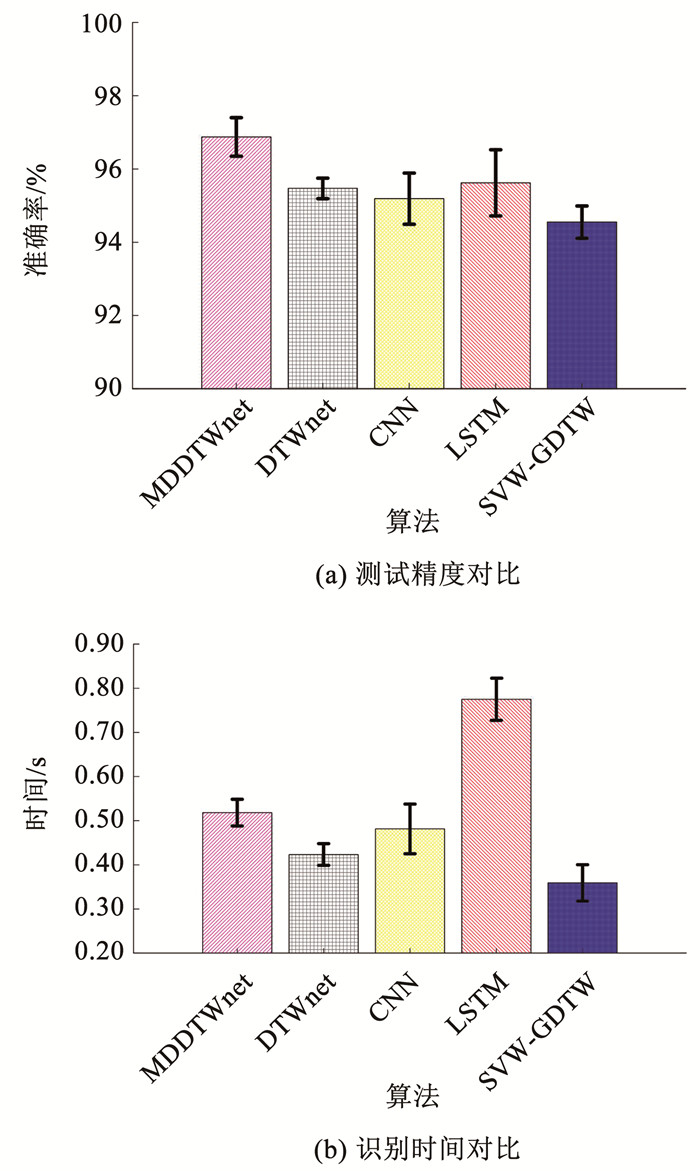
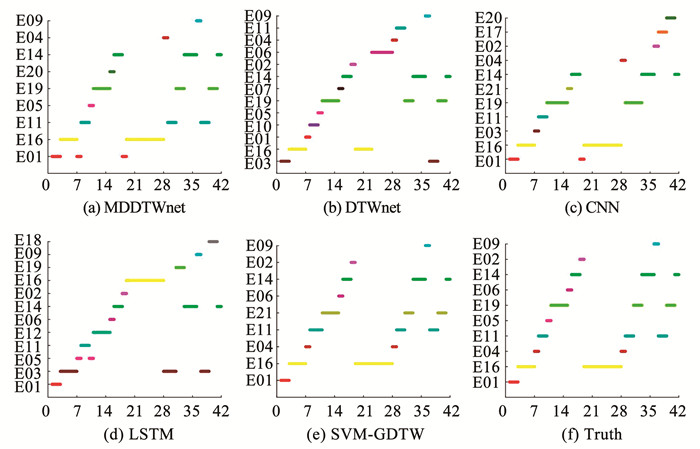
不同识别方法仿真测试结果见表 2和图 7。表 2统计了20次训练过程的识别精度与识别时间均值与方差。从表 2可以看出,MDDTWnet获得了较高的识别精度,说明基于马氏距离度量的动态规整对齐策略对识别精度有提高作用。MDDTWnet与DTWnet的方差总体上较小,说明动态时间规整神经网络具有鲁棒性;在识别时间方面,SVM-GDTW消耗的识别时间是最少的。
| 表 2 不同识别方法仿真测试结果统计 Tab. 2 Simulation test statistics results of different recognition methods |
|
图 7 不同方法在机动轨迹单元库仿真中的识别结果对比 Fig. 7 Comparison of recognition results in simulation of different methods on maneuver trajectory unit library |
图 7给出了20次训练过程之后测试样本识别精度与识别时间带有误差棒的条形图。如图 7所示,虽然MDDTWnet花费的时间比DTWnet、CNN、SVM-GDTW多,但是识别精度是最好的。测试样本有1 050个,则MDDTWnet平均每个样本的测试识别时间为4.96 ms,满足在线识别实时要求。测试综上所述,由于马氏距离的计算,MDDTWnet花费的时间相对较多,但是满足实时性,且其识别精度是最好的。
下式给出了机动轨迹单元训练样本的马氏矩阵MDTW。通过表 2比较MDDTWnet、DTWnet,MDDTWnet的识别准确率优于DTWnet,证明了马氏距离度量的有效性。图 8给出了基于MDDTW度量的机动轨迹单元库部分样本马氏距离。通过观察,样本库马氏距离的对角线的颜色深于矩阵其他部分,说明其度量学习结果表现较好。
| $ \boldsymbol{M}_{\text {DTW }}=\left[\begin{array}{rrrrrrrr} 0.000658 & -0.006500 & -0.000536 & 0.005400 & 0.002600 & 0.000103 & -0.000243 \\ -0.006500 & 0.112800 & 0.026500 & 0.085500 & -0.104900 & -0.003200 & 0.027200 \\ -0.000536 & 0.026500 & 0.074300 & 0.362200 & -0.324300 & -0.005600 & 0.025600 \\ 0.005400 & 0.085500 & 0.362200 & 5.155500 & -1.369000 & -0.022300 & 0.097100 \\ 0.002600 & -0.104900 & -0.324300 & -1.369000 & 1.521300 & 0.026900 & -0.127600 \\ 0.000103 & -0.003200 & -0.005600 & -0.022300 & 0.026900 & 0.001200 & -0.011100 \\ -0.000243 & 0.027200 & 0.025600 & 0.097100 & -0.127600 & -0.011100 & 0.134200 \end{array}\right] $ | (33) |

|
图 8 基于MDDTW度量的机动轨迹单元库部分样本马氏距离 Fig. 8 Mahalanobis distance of partial samples of maneuver trajectory unit library based on MDDTW |
为进一步验证基于MDSVM-MDDTWnet在线机动轨迹识别方法的有效性与鲁棒性,本文从空战对抗数据库[26-27]中选取3段机动轨迹工况进行仿真。
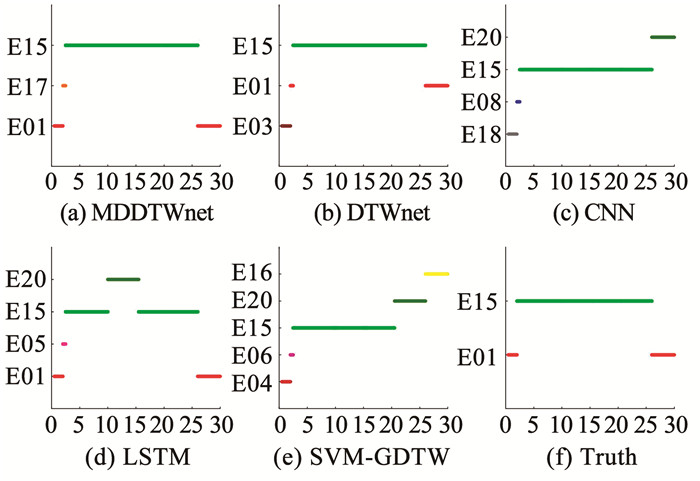
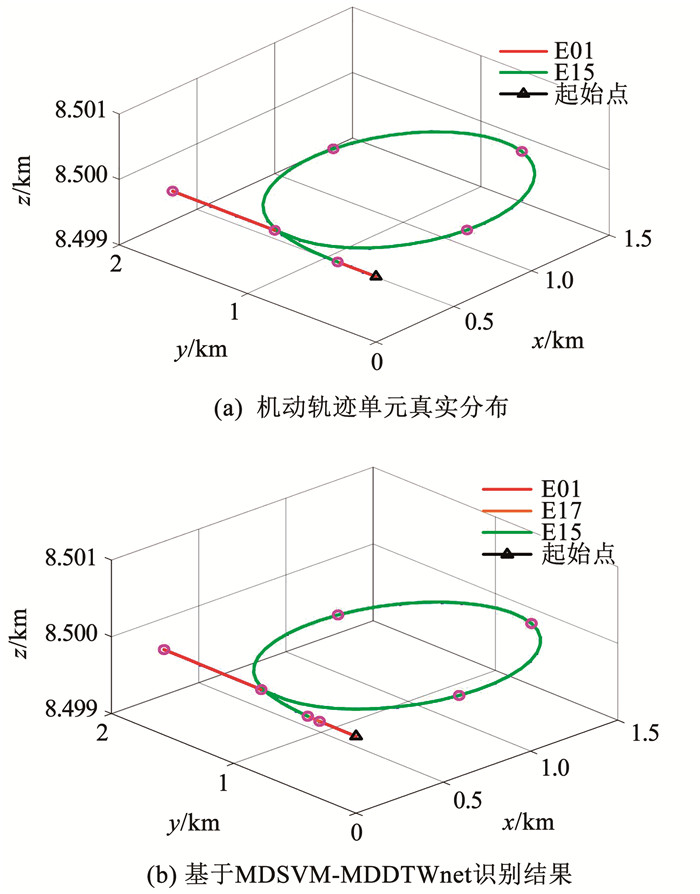
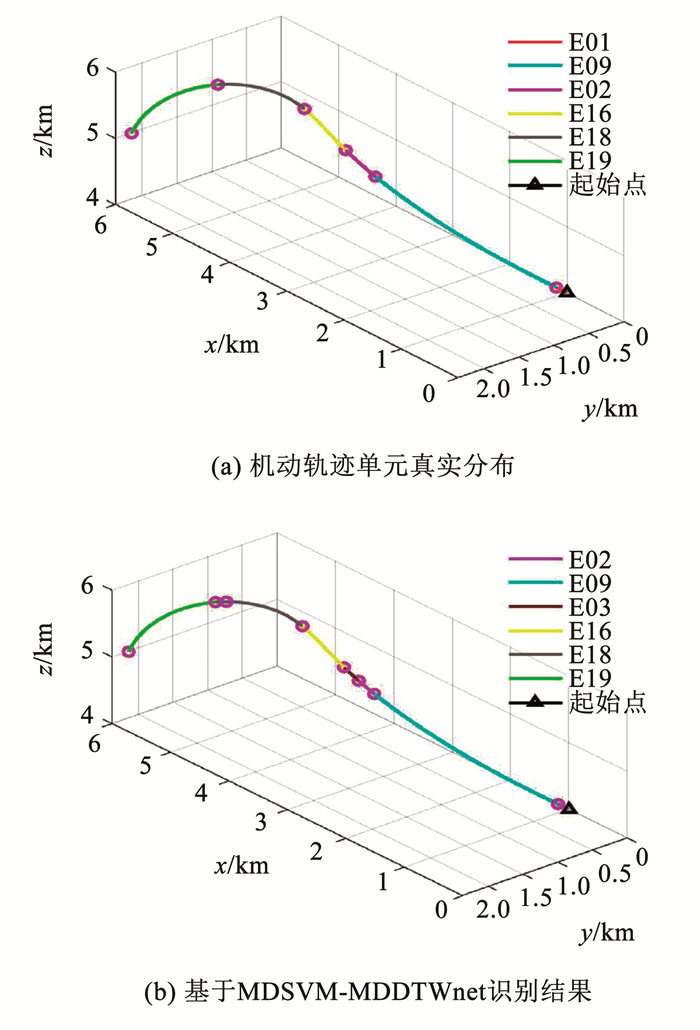
6.3.1 工况1 : 水平右转盘旋机动识别仿真水平右盘旋轨迹机动的识别仿真结果见图 9、10。图 9给出了MDSVM分割后不同识别算法的识别结果。MDDTWnet将误分的分割点视为机动轨迹单元E17,同时,其识别结果与真实机动轨迹单元分布情况相似。DTWnet除了误分分割点,还将第1段轨迹单元误分为E03;CNN将第1段与最后1段误分为E18与E20;LSTM将第3段轨迹单元误分为E20;SVM-GDTW识别效果是最差的,误分3段轨迹单元。为进一步形象地刻画轨迹分割情况,图 10给出了原始分割识别图与基于MDSVM-MDDTWnet的分割识别图。从图 10可以看出,基于MDSVM-MDDTWnet的识别与原始分布情况很相似,仅仅在第1段轨迹之后的点误分割,导致将其识别为机动轨迹单元E17。
|
图 9 水平右转盘旋机动识别结果对比 Fig. 9 Comparisons of recognition results for horizontal right turn circling maneuver |
|
图 10 水平右转盘旋机动真实分布与识别的轨迹对比 Fig. 10 Trajectory comparisons for real distribution and recognition results for horizontal right turn circling maneuver |
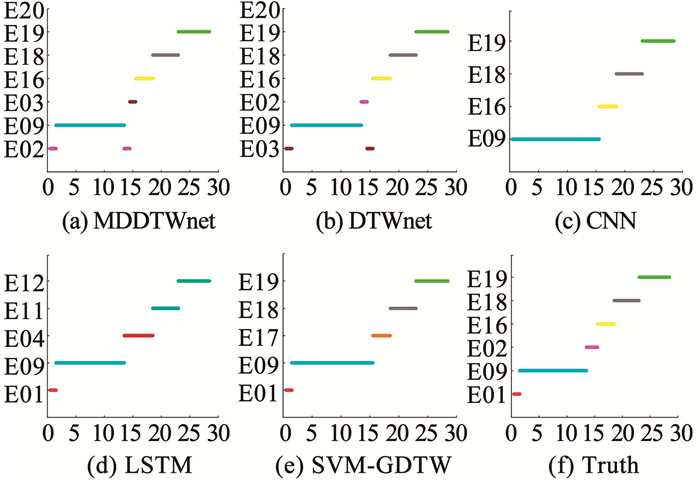
滚转剪式轨迹机动的识别仿真结果见图 11、12。图 11给出了MDSVM分割后不同识别算法的识别结果。从图 11可以看出,MDDTWnet识别结果与真实机动轨迹单元分布情况相似。由于在线分割点误检测,将13.5~14.5 s之间的机动轨迹误分为E02,但是对22.5~23.0 s之间的机动轨迹识别结果与原始轨迹类别一样,同为E18。为进一步形象地刻画轨迹分割情况,图 12给出了原始分割识别图与基于MDSVM-MDTWnet的分割识别图。从图 12可以看出,基于MDSVM-MDDTWnet的识别与原始分布情况很相似,但是有两处误分割点,第1个误分割点导致机动轨迹单元识别错误。
|
图 11 滚转剪式机动识别结果对比 Fig. 11 Comparisons of recognition results for rolling scissor motor maneuver |
|
图 12 滚转剪式机动真实分布与识别的对比 Fig. 12 Trajectory comparisons of real distribution and recognition results for rolling scissor motor maneuver |
长时域复杂机动的识别仿真结果见图 13、14。图 13给出了MDSVM分割后不同识别算法的识别结果。从图 13可以看出,MDDTWnet将7~8 s之间的机动轨迹单元E04误分为E01,将18~19 s之间的机动轨迹单元E02误分为E01。为进一步形象地刻画轨迹分割情况,图 14给出了原始空间轨迹分割识别图与基于MDSVM-MDDTWnet的空间轨迹分割识别图。
|
图 13 长时域复杂机动识别结果对比 Fig. 13 Comparisons of recognition results for long-time domain complex maneuver |

|
图 14 水平右转盘旋机动真实分布与识别的轨迹对比 Fig. 14 Trajectory comparisons of real distribution and recognition results for long-time domain complex maneuver |
上述两种机动轨迹中不同算法的在线分割识别率与时间代价统计见表 3。从表 3可以看出,MDDTWnet的在线分割识别率是最高的,SVM-GDTW在线识别时间代价中是最少的。虽然,MDDTWnet时间代价较高,但是满足在线识别的实时性,两个工况的机动轨迹平均每一秒识别代价分别是1.20、3.14 ms。上述分析可知,MDSVM-MDDTWnet在线分割识别系统在满足在线识别实时性的同时具有较高识别准确率。
| 表 3 不同机动轨迹中不同算法的在线分割识别率与时间代价 Tab. 3 Online segmentation recognition rate and time cost of different algorithms in different maneuver trajectory cases |
1) 基于MDSVM的机动轨迹分割点检测方法准确率较高;与其他识别方法对比,基于MDDTWnet的机动轨迹单元识别方法在满足实时性的同时,识别精度是最好的。
2) 3种工况下的机动轨迹分割识别仿真实验结果表明融合的在线机动分割识别方法具有有效性、鲁棒性与实时性。
3) 由于马氏距离的计算,MDDTWnet花费的时间相对较多,进一步提高在线识别的实时性将是下一步研究的重点。另外,当前分割点检测模型和机动轨迹单元识别模型都是离线训练在线识别,离线训练需要耗费较多的时间,且不能够实时地构建识别模型,使得识别模型不够泛化,因此提高训练模型时间是下一步研究关键点。
| [1] |
贾镇泽, 樊晓光, 薛明浩, 等. 基于机动动作元的敌机战术机动在线识别方法[J]. 北京理工大学学报, 2018, 38(8): 820. JIA Zhenze, FAN Xiaoguang, XUE Minghao, et al. Online identification method for tactical maneuver of target based on air combat maneuver element[J]. Transactions of Beijing Institute of Technology, 2018, 38(8): 820. DOI:10.15918/j.tbit1001-0645.2018.08.009 |
| [2] |
徐西蒙, 杨任农, 于洋, 等. 基于运动分解和H-SVM的空战目标机动识别[J]. 控制与决策, 2020, 35(5): 1265. XU Ximeng, YANG Rennong, YU Yang, et al. Target maneuver recognition in air combat based on motion decomposition and H-SVM[J]. Control and Decision, 2020, 35(5): 1265. DOI:10.13195/j.kzyjc.2018.1210 |
| [3] |
梅江元. 基于马氏距离的度量学习算法研究及应用[D]. 哈尔滨: 哈尔滨工业大学, 2016 MEI Jiangyuan. Research on Mahalanobis distance based metric learning algorithm and its applications[D]. Harbin: Harbin Institute of Technology, 2016 |
| [4] |
周超, 樊蓉, 张戈, 等. 基于多元时间序列融合的飞行动作识别方法[J]. 空军工程大学学报(自然科学版), 2017, 18(4): 34. ZHOU Chao, FAN Rong, ZHANG Ge, et al. A flight action recognition based on multivariate time series fusion[J]. Journal of Air Force Engineering University (Natural Science Edition), 2017, 18(4): 34. DOI:10.3969/j.issn.1009-3516.2017.04.007 |
| [5] |
姚佩阳, 周旺旺, 张杰勇, 等. 基于动态时间规整的空中目标机动识别[J]. 火力与指挥控制, 2018, 43(9): 15. YAO Peiyang, ZHOU Wangwang, ZHANG Jieyong, et al. Aerial target maneuvering recognition based on dynamic time warping[J]. Fire Control & Command Control, 2018, 43(9): 15. DOI:10.3969/j.issn.1002-0640.2018.09.004 |
| [6] |
WEI Zhenglei, DING Dali, ZHOU Huan, et al. A flight maneuver recognition method based on multi-strategy affine canonical time warping[J]. Applied Soft Computing, 2020, 95: 106527. DOI:10.1016/j.asoc.2020.106527 |
| [7] |
倪世宏, 史忠科, 谢川, 等. 军用战机机动飞行动作识别知识库的建立[J]. 计算机仿真, 2005, 22(4): 23. NI Shihong, SHI Zhongke, XIE Chuan, et al. Establishment of avion inflight maneuver action recognizing knowledge base[J]. Computer Simulation, 2005, 22(4): 23. DOI:10.3969/j.issn.1006-9348.2005.04.007 |
| [8] |
XIAO Qinkun, SONG Ren. Action recognition based on hierarchical dynamic Bayesian network[J]. Multimedia Tools and Applications, 2018, 77(6): 6955. DOI:10.1007/s11042-017-4614-0 |
| [9] |
ZHAO Bendong, LU Huanzhang, CHEN Shangfeng, et al. Convolutional neural networks for time series classification[J]. Journal of Systems Engineering and Electronics, 2017, 28(1): 162. DOI:10.21629/JSEE.2017.01.18 |
| [10] |
LI Wenbo, WEN Longyin, CHANG M C, et al. Adaptive RNN tree for large-scale human action recognition[C]//2017 IEEE International Conference on Computer Vision (ICCV). Venice: IEEE, 2017: 1453. DOI: 10.1109/ICCV.2017.161
|
| [11] |
ISMAIL FAWAZ H, FORESTIER G, WEBER J, et al. Deep learning for time series classification: a review[J]. Data Mining and Knowledge Discovery, 2019, 33(4): 917. DOI:10.1007/s10618-019-00619-1 |
| [12] |
ISMAIL FAWAZ H, FORESTIER G, WEBER J, et al. Deep neural network ensembles for time series classification[C]//2019 International Joint Conference on Neural Networks (IJCNN). Budapest: IEEE, 2019: 1. DOI: 10.1109/IJCNN.2019.8852316
|
| [13] |
赵智伟, 袁伟伟, 关东海. 基于Multivariate BiLSTM-FCNs的机动实时识别方法[J]. 航空计算技术, 2023, 53(2): 65. ZHAO Zhiwei, YUAN Weiwei, GUAN Donghai. A real-time identification method for maneuvers based on multivariate BiLSTM-FCNs[J]. Aeronautical Computing Technique, 2023, 53(2): 65. DOI:10.3969/j.issn.1671-654X.2023.02.014 |
| [14] |
CHENG Hua, XIE Lei, TANG Shangqin, et al, Maneuvering trajectory recognition based on COA-LSSVM[C]//Proceedings of the 6th International Workshop on Advanced Algorithms and Control Engineering (IWAACE 2022). Qingdao: SPIE, 2022. DOI: 10.1117/12.2652492
|
| [15] |
平宏达, 刘义海, 单连平. 基于双驱动模型的目标机动行为识别方法[J]. 指挥控制与仿真, 2023, 45(2): 88. PING Hongda, LIU Yihai, SHAN Lianping. Target maneuver behavior recognition method based on double drive model[J]. Command Control & Simulation, 2023, 45(2): 88. DOI:10.3969/j.issn.1673-3819.2023.02.014 |
| [16] |
孔波, 陈坤杰, 李品, 等. 空中目标自适应分段轨迹样式识别[J]. 现代雷达, 2023, 45(2): 39. KONG Bo, CHEN Kunjie, LI Pin, et al. Adaptive segmental trajectory pattern recognition of aerial targets[J]. Modern Radar, 2023, 45(2): 39. DOI:10.16592/j.cnki.1004-7859.2023.02.007 |
| [17] |
张夏阳, 殷之平, 刘飞, 等. 飞机机动划分的数据挖掘方法[J]. 西北工业大学学报, 2016, 34(1): 33. ZHANG Xiayang, YIN Zhiping, LIU Fei, et al. An aircraft maneuver partition method based on data mining[J]. Journal of Northwestern Polytechnical University, 2016, 34(1): 33. DOI:10.3969/j.issn.1000-2758.2016.01.005 |
| [18] |
徐琴珍, 杨绿溪. 一种基于有监督局部决策分层支持向量机的异常检测方法[J]. 电子与信息学报, 2010, 32(10): 2383. XU Qinzhen, YANG Lüxi. A supervised local decision hierachical support vector machine based anomaly intrusion detection method[J]. Journal of Electronics & Information Technology, 2010, 32(10): 2383. DOI:10.3724/SP.J.1146.2010.00321 |
| [19] |
ZHOU Feng, DE LA TORRE F, HODGINS J K. Aligned cluster analysis for temporal segmentation of human motion[C]//2008 8th IEEE International Conference on Automatic Face & Gesture Recognition. Amsterdam: IEEE, 2008: 1. DOI: 10.1109/AFGR.2008.4813468
|
| [20] |
HE H, GARCIA E A. Learning from imbalanced data[J]. IEEE Transactions on Knowledge & Data Engineering, 2009, 21(9): 1263. DOI:10.1109/TKDE.2008.239 |
| [21] |
PLATT J C. Using analytic QP and sparseness to speed training of support vector machines[C]//Proceedings of the 11th International Conference on Neural Information Processing Systems. Denver: ACM, 1998: 557. DOI: 10.5555/3009055.3009134
|
| [22] |
ZHOU Zhiyu, ZHANG Ruoxi, WANG Yaming, et al. Color difference classification based on optimization support vector machine of improved grey wolf algorithm[J]. Optik, 2018, 170: 17. DOI:10.1016/j.ijleo.2018.05.096 |
| [23] |
WANG Zhiguang, YAN Weizhong, OATES T. Time series classification from scratch with deep neural networks: a strong baseline[C]//2017 International Joint Conference on Neural Networks (IJCNN). Anchorage: IEEE, 2017: 1578. DOI: 10.1109/IJCNN.2017.7966039
|
| [24] |
ZHENG Yi, LIU Qi, CHEN Enhong, et al. Time series classification using multi-channels deep convolutional neural networks[C]//International Conference on Web-Age Information Management. Cham: Springer, 2014: 298. DOI: 10.1007/978-3-319-08010-9_33
|
| [25] |
MEI Jiangyuan, LIU Meizhu, WANG Yuanfang, et al. Learning a mahalanobis distance-based dynamic time warping measure for multivariate time series classification[J]. IEEE Transactions on Cybernetics, 2016, 46(6): 1363. DOI:10.1109/TCYB.2015.2426723 |
| [26] |
KINGMA D P, BA J. Adam: a method for stochastic optimization[EB/OL]. 2014: 1412.6980. http://arxiv.org/abs/1412.6980v9
|
| [27] |
IOFFE S, SZEGEDY C. Batch normalization: accelerating deep network training by reducing internal covariate shift[C]//Proceedings of the 32nd International Conference on International Conference on Machine Learning. Lillez: Proceedings of Machine Learning Research, 2015: 448. DOI: 10.48550/arXiv.1502.03167
|
| [28] |
ZAZO R, LOZANO-DIEZ A, GONZALEZ-DOMINGUEZ J, et al. Language identification in short utterances using long short-term memory (LSTM) recurrent neural networks[J]. PLoS One, 2016, 11(1): e0146917. DOI:10.1371/journal.pone.0146917 |
| [29] |
BAHLMANN C, HAASDONK B, BURKHARDT H. Online handwriting recognition with support vector machines-a kernel approach[C]//Proceedings Eighth International Workshop on Frontiers in Handwriting Recognition. Niagra-on-the-Lake: IEEE, 2002: 49. DOI: 10.1109/IWFHR.2002.1030883
|
| [30] |
谢磊, 丁达理, 魏政磊, 等. AdaBoost-PSO-LSTM网络实时预测机动轨迹[J]. 系统工程与电子技术, 2021, 43(6): 1651. XIE Lei, DING Dali, WEI Zhenglei, et al. Real time prediction of maneuver trajectory for AdaBoost-PSO-LSTM network[J]. Systems Engineering and Electronics, 2021, 43(6): 1651. DOI:10.12305/j.issn.1001-506X.2021.06.23 |
| [31] |
XIE Lei, WEI Zhenglei, DING Dali, et al. Long and short term maneuver trajectory prediction of UCAV based on deep learning[J]. IEEE Access, 2021, 9: 32321. DOI:10.1109/ACCESS.2021.3060783 |
 2024, Vol. 56
2024, Vol. 56


