2. 甘肃省轨道交通电气自动化工程实验室,兰州 730070
2. Rail Transit Electrical Automation Engineering Laboratory of Gansu Province, Lanzhou 730070, China
兰新高铁横跨多个省区,全长1 775.779 km,是中国乃至世界上穿越最长沙漠和风区的高速铁路,其在新疆自治区内途径达坂城、三十里、百里和烟墩风区,在甘肃境内途经安西风区,五大风区内线路总长达579.599 km[1-2]。风区内环境恶劣、大风频发,对高铁沿线设施和列车安全行车造成严重危害。为确保高速列车运行稳定,在风区内高铁路基的迎风侧设置了挡风墙。挡风墙对来风存在明显加速作用,导致挡风墙背风侧附加导线发生剧烈舞动现象,一方面容易引起附加导线绝缘距离不足,导致线间放电造成变电所跳闸故障; 另一方面容易导致线夹处连接金具磨损、导线疲劳断股,造成掉线等事故[3-4],严重影响兰新高铁安全运行。
兰新高铁大风区段接触网附加导线的舞动主要发生在无覆冰情况下。来风在经过路基以及挡风墙后在附加导线所处区域形成增速区并产生一定仰角,极大改变了附加导线气动特性。风能转化为附加导线自身振动的能量,使得附加导线发生剧烈舞动[5-6],现场附加导线舞动见图 1。因此,分析附加导线发生舞动的条件,得到附加导线舞动时线间最小间距离与档距、运行张力、阻尼比等因素之间的关系,并提出有效可行的防治措施,对保障大风区高速铁路安全意义重大。

|
图 1 大风区段兰新高铁接触网附加导线舞动 Fig. 1 Additional conductors galloping of Lanzhou-Xinjiang high-speed railway OCS in strong wind section |
目前,国内外学者针对输电导线舞动问题进行了大量研究。文献[7]建立了五分裂导线有限元模型,分析了湍流风作用下的上游导线尾流对下游导线气动特性及运动轨迹的影响,得到了分裂导线动态响应规律。文献[8]利用风洞装置对覆冰分裂导线进行舞动试验,研究了导线气动阻尼与风速、气动特性、自振特性的关系,并提出了三自由度体系稳定性判据公式。文献[9]运用覆冰四分裂导线模型和拉索相结合的方式,提出了一种考虑输电线路几何非线性特征的舞动试验模型,并通过实验和仿真相结合的方式验证了该试验模型。文献[10]建立了覆冰分裂导线非线性有限元方程,并编写了计算程序,模拟了不同档距对四分裂导线舞动幅值和模式的影响。文献[11]通过风洞试验与有限元软件模拟了覆冰四分裂及八分裂导线的气动特性,分析了上游子导线尾流对下游子导线的气动系数的影响。文献[12]建立了1 000 kV特高压紧凑型输电线路导线-绝缘子串耦合有限元模型,分析不同工况下的舞动响应,总结了导线舞动时最小相间距离与风速、覆冰厚度、档距等因素之间的变化关系。文献[13]建立了连续档线路有限元模型,对比分析了单档和多档导线舞动特征,得出单档和多档导线舞动特征存在明显差异。文献[14]推导了导线体系舞动常微分方程,对比分析了导线在匀减速风场和骤停风场下的舞动响应,得到了其舞动响应规律。既有研究基于分裂导线、气动阻尼、档距、导线尾流、风场等因素对电力系统覆冰线路的舞动特性开展了试验与仿真研究。由于兰新高铁挡风墙对来流的汇聚加速作用, 挡风墙背面侧接触网附加导线在无覆冰环境下发生舞动, 并非覆冰舞动[15]。并且铁路系统中接触网附加导线结构以及工作环境较为特殊,电力输电线舞动分析理论及防舞经验并不完全适用于铁路接触网。为了保障高速电气化铁路牵引供电系统的安全运行,亟需对大风环境下接触网附加导线的舞动特性及其影响因素进行深入研究。
本文结合接触网附加导线的结构特点,建立附加导线有限元模型,采用谐波叠加法模拟接触网附加导线处的随机风场,并对导线模型施加风荷载,利用无条件稳定Newmark法以及荷载增量法,分析接触网线路参数对附加导线舞动及线间距离的影响规律,并给出相应的防治措施。研究成果可为兰新高铁大风区段接触网附加导线舞动导致的断线、线间放电等问题提供更加合理、有效的解决方案,为大风区段接触网附加导线的抗风设计提供一定理论依据。
1 接触网附加导线有限元建模兰新高速铁路采用自耦变压器供电方式(AT供电方式),沿接触网线路架设正馈线和保护线,正馈线对地电压高达27.5 kV,保护线接地。两线发生舞动时,线间距离发生变化,容易导致放电。兰新高速铁路接触网线路结构见图 2。

|
图 2 兰新高速铁路接触网线路结构 Fig. 2 OCS structure of Lanzhou-Xinjiang high-speed railway |
接触网附加导线的初始平衡状态是求解其动力响应的基础,在对附加导线进行舞动分析之前,须对接触网附加导线在自重作用下的初始构型进行计算,得到其达到静平衡时的位置和应力[16-17]。导线力学的计算方法主要有悬链线法和抛物线法,悬链线法在求解导线相关方程时涉及双曲函数,计算过程过于繁琐,所以在工程应用中,通常使用更加简便的抛物线法来计算。
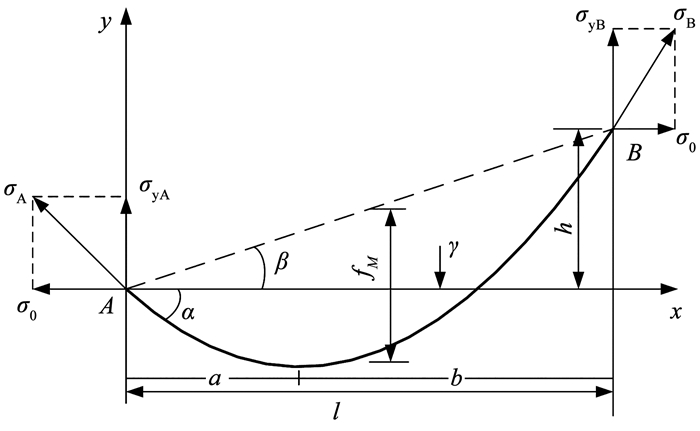
图 3为导线近似平抛物线受力。在二维坐标平面内,导线的一端A点位于原点,另一端为B点,两点间在竖直方向的投影距离为悬挂点高差h,在兰新高铁接触网附加导线建设中,附加导线的两端悬挂点基本无高差,且档距较小,假定附加导线的比载γ(单位截面上承受的荷载)沿档距均匀分布,故使用平抛物线公式对导线在自重条件下进行分析。
|
图 3 导线近似平抛物线受力 Fig. 3 Force of conductor approximating to a flat parabola |
根据表 1附加导线参数可以计算得到正馈线及保护线单位长度自重荷载分别为11.13 N/m和6.80 N/m,按照兰新高铁接触网附加导线的施工安装曲线,即可得到正馈线及保护线初始张力。
| 表 1 附加导线参数 Tab. 1 Parameters of additional conductors |
利用有限元软件建立接触网附加导线模型, 正馈线和保护线均每隔1 m划分一个单元,设置两导线悬挂处为固定约束,忽略沿跨度方向的阻尼。导线只承受拉力和自身重力,不承受压力和弯矩,故正馈线及保护线均采用LINK10单元来模拟,并设定该单元仅受拉力以模拟悬索的松弛状态,计算导线在均布自重荷载及水平张力作用下的曲线形状,找形后的接触网附加导线有限元模型见图 4。
|
图 4 接触网附加导线有限元模型 Fig. 4 Finite element model of OCS additional conductors |
将平抛物线法与有限元法计算得到的接触网附加导线应力进行对比, 2种方法计算结果差别小于0.6%,验证了本文建立的接触网附加导线有限元模型的正确性。
2 附加导线气动特性分析及风洞试验 2.1 挡风墙影响下附加导线气动特性分析通过流体计算软件求解路基挡风墙影响下附加导线气动特性,选择Transition SST四方程转捩模型来模拟接触网附加导线的气动特性,可以精准预测湍流度、流动分离和压力梯度的变化。
1) 质量守恒方程
质量守恒方程的表达式为
| $ \frac{\partial \rho}{\partial t}+\frac{\partial(\rho u)}{\partial x}+\frac{\partial(\rho v)}{\partial y}=0 $ | (1) |
式中: u、v分别为风速矢量在x、y方向上的分量,ρ、t分别为密度和时间。
空气速度对密度的影响可以忽略,用不可压缩流体模型,则质量守恒方程为
| $ \frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0 $ | (2) |
2) 动量守恒方程
动量守恒定律也称牛顿第二定律,为微元体上的各种力之和等于微元体中流体动量随时间的变化率,动量守恒的数学表达式(x、y方向)为:
| $ \left\{\begin{array}{l} \frac{\partial(\rho u)}{\partial t}+\frac{\partial(\rho u u)}{\partial x}+\frac{\partial(\rho u v)}{\partial y}= \\ \quad \frac{\partial}{\partial x}\left(u \frac{\partial(u)}{\partial x}\right)+\frac{\partial}{\partial y}\left(u \frac{\partial(u)}{\partial y}\right)-\frac{\partial p}{\partial x}+S_u \\ \frac{\partial(\rho v)}{\partial t}+\frac{\partial(\rho v u)}{\partial x}+\frac{\partial(\rho v v)}{\partial y}= \\ \frac{\partial}{\partial x}\left(u \frac{\partial(v)}{\partial x}\right)+\frac{\partial}{\partial y}\left(u \frac{\partial(v)}{\partial y}\right)-\frac{\partial p}{\partial x}+S_v \end{array}\right. $ | (3) |
式中:Sv=Fx+Sx、Su=Fv+Sy是动量守恒方程的广义源项;Fx、Fy分别为微元体x、y方向上的体积力;对于不可压缩流体来说Sx=Sy=0;p为压力。
图 5为路基挡风墙、附加导线网格及边界示意,为更好模拟导线周围流场,选择结构化网格,对整体模型进行分块划分,在导线以及挡风墙的近壁面进行适当加密,并对导线周围近壁面采用“O”型网格划分,使得第一层网格的y+≈1。
|
图 5 路基挡风墙、附加导线网格及边界示意 Fig. 5 Schematic of subgrade wind retaining wall and additional conductors grid and boundary |
流体仿真中采用SIMPLEC算法模拟压力速度的耦合,动量为二阶迎风格式,压力方程为二阶精确度离散格式,计算的时间设置为5 s,计算时间步长为0.005 s。图 6为入口风速为15 m/s时模型计算域风速云图。来风在经过挡风墙过程中,出现边界层分离,在挡风墙背风侧产生巨大旋涡,使得挡风墙尾流区域风速急剧增大,导线周围流场分布较为复杂。根据有/无挡风墙条件下附加导线气动特性的研究发现,无墙条件下附加导线区域流场较为稳定。可见挡风墙对来风的汇聚是接触网附加导线发生剧烈舞动的重要原因。

|
图 6 模型计算域风速云图 Fig. 6 Wind speed cloud diagram of model computational domain |
挡风墙后附加导线的风攻角、风速放大系数与风速的关系见表 2。附加导线位置处风攻角及风速放大系数随入口风速存在明显规律,正馈线位置处的风速一般约为入口风速的2.2倍,风攻角在15 m/s后达到稳定,基本在30°左右。保护线位置处风攻角及风速放大系数较为稳定,风速约为入口风速的1.2倍,风攻角基本在20°左右。附加导线升、阻力系数与风速的关系见表 2。随着风速增大,正馈线升、阻力系数呈减小趋势。
| 表 2 不同入口风速下附加导线处风参数及气动系数 Tab. 2 Wind parameters and aerodynamic coefficients at additional conductors under different inlet wind speeds |
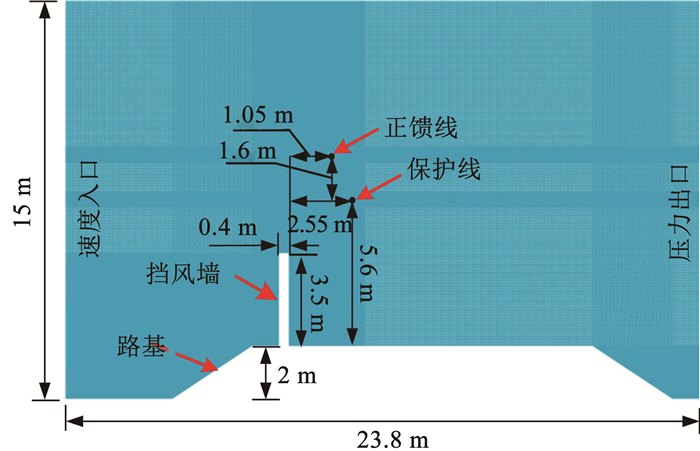
试验采用低速风洞,风速最高为30 m/s。试验段采用305 mm×305 mm的方形截面,基于相似原理设计并制作挡风墙及接触网附加导线的试验模型见图 7。试验模型中正馈线高度为155.56 mm,保护线高度为94.69 mm,路堤坡度为1∶1.5,路堤高为33.82 mm,挡风墙高为59.18 mm,整体模型的几何相似比为1∶59。利用风速测量仪测量挡风墙后导线处的风速变化,图 8为风速测量装置。

|
图 7 风洞试验模型 Fig. 7 Wind tunnel test model |

|
图 8 风速测量仪 Fig. 8 Anemometer |
利用流体仿真软件,对不同入口风速下缩尺仿真模型中挡风墙后方附加导线位置处的风速进行监测[18]。以正馈线处风速为例,试验与仿真结果对比见表 3。从中可以看出,挡风墙对导线位置处气流存在汇聚加速作用,试验与仿真结果的差别在合理范围,主要由风洞气密性及测量仪器精度原因导致。本文所采用的流体仿真方法的正确性与合理性得到了充分验证。
| 表 3 风洞试验与仿真结果对比 Tab. 3 Comparison of wind tunnel test and simulation results |
接触网附加导线舞动的基本方程为:
| $ \boldsymbol{M} \ddot{\boldsymbol{u}}+\boldsymbol{C} \dot{\boldsymbol{u}}+\boldsymbol{K} \boldsymbol{u}=\{\boldsymbol{F}(t)\} $ | (4) |
式中:
在接触网附加导线舞动模拟中,利用无条件稳定的Newmark法和荷载增量法来计算导线的非线性动力平衡方程,将附加导线所受荷载分成若干个增量,并对每一载荷增量的非线性方程进行线性化,将导线的非线性动力学问题转化为线性问题,最终计算得到接触网附加导线的舞动响应。
3.2 风场模拟本文选择谐波叠加法(WAWS法)来模拟接触网附加导线处的随机风场。随机风包含平均风和脉动风两部分[19]。通过气动特性分析及风洞试验的结论,对正馈线以及保护线悬挂点处风速、平均风速模拟函数分别进行了相应的修正。考虑挡风墙影响下附加导线悬挂点处平均风速U(h)与10 m高处基本风速v10之间存在指数关系如下式:
| $ \bar{U}(h)=K \bar{v}_{10}\left(\frac{h}{10}\right)^\alpha $ | (5) |
式中:K为挡风墙后附加导线悬挂点处风速放大修正系数,h为附加导线悬挂点高度,α为风速剖面指数,以附加导线舞动最为剧烈的百里风区为例,该地区为B类地貌,取0.15。
由于接触网附加导线档距比电力输电线路档距小,不同受风点之间的高度差也较小,故目标谱采用Davenport风速谱,表达式如下:
| $ S_v(n)=\bar{v}_{10}^2 \frac{4 k x^2}{n\left(1+x^2\right)^{4 / 3}} $ | (6) |
式中: k为地面粗糙度系数,取0.005;x=1 200 n/v10;n为脉动风频率;Sv(n)则为脉动风速功率谱。
风速模拟点坐标取正馈线和保护线悬挂点处,模拟时程总长为800 s,时间步长为0.2 s,截止频率为1 Hz,频率范围等分数为2 048。当入口平均风速为15 m/s时,模拟得出附加导线悬挂点处的风速时程曲线见图 9。

|
图 9 接触网附加导线风速时程曲线 Fig. 9 Wind speed time history curves of OCS additional conductors |
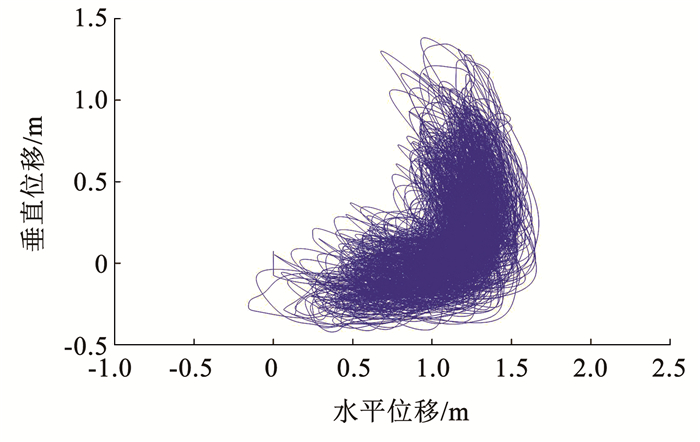
导线舞动振型和档距长度具有一定相关性,档距越小,舞动的半波数越少。由现场调研,接触网附加导线基本无高差,档距长度多在60 m以下,舞动形态主要为单半波舞动。在模拟计算中,以15 m/s风速为例,为了保证计算结果的稳定性及收敛性,将仿真模拟时间设置为800 s。以50 m档距为例计算附加导线舞动响应,正馈线和保护线张力分别设置其初始张力3 381 N、2 205 N,阻尼比设置为0.4%。图 10和图 11为50 m档距下附加导线舞动轨迹曲线。从中可以看出,正馈线和保护线的舞动位移规律基本类似,两导线均在起始阶段发生微幅振动,并在水平方向发生一定偏移。随时间的持续,舞动越发剧烈,垂向及水平位移曲线呈波浪式增加和减小,表现出一定随机性特征。在舞动过程中,舞动仅在一定时间内达到稳定,其余时间一直处于非稳定状态,正馈线及保护线舞动轨迹均近似斜椭圆,且正馈线振幅明显高于保护线,与百里风区接触网附加导线舞动现场情况基本相同。
|
图 10 50 m档距下正馈线舞动轨迹 Fig. 10 Galloping track of positive feeder under 50 m span |

|
图 11 50 m档距下保护线舞动轨迹 Fig. 11 Galloping track of protection line under 50 m span |
根据现场实际在有限元软件中分别建立跨距为35 m、40 m、45 m、50 m和55 m的附加导线模型,正馈线和保护线分别设置其初始张力3 381 N、2 205 N,阻尼比设置为0.4%,得到不同跨距长度附加导线的舞动响应结果。不同档距下附加导线垂向及水平振幅变化趋势见图 12(a)。从图 12(a)可以看出,35 m及40 m档距下正馈线仅发生小幅摇摆,垂向及水平振幅基本低于1.04 m,保护线垂向及水平振幅低于1.4 m,45~55 m档距下正馈线及保护线舞动强度明显增强。可见,随着档距减小,正馈线垂向及水平振幅不断减小,这是因为档距降低,导线等效静刚度增大,同时导线吸收的能量也就越少。通过对不同档距下接触网附加导线振幅变化趋势分析可以得出,35 m和40 m档距附加导线在不同风速下的振幅较为稳定,具有明显的抑舞效果,50 m和55 m档距下附加导线的舞动幅值较大。因此,对大风区段接触网附加导线设计时,应尽量选择40 m及更小档距。

|
图 12 不同线路参数下附加导线振幅 Fig. 12 Additional conductor amplitude under different line parameters |
导线在自重作用下达到静平衡时的张力为运行张力。随着运行张力增加,导线刚度也相应增大,可有效抑制导线的振动效应。为分析接触网附加导线运行张力对舞动幅值的影响,档距设置为50 m,正馈线和保护线运行张力分别为其初始张力3 381 N、2 205 N,并将两导线运行张力分别增大至4 500 N、5 500 N、6 500 N、7 500 N进行计算,得到不同运行张力下附加导线振幅变化趋势见图 12(b)。从图 12(b)可以看出,随运行张力增大,正馈线及保护线振幅整体呈现下降趋势,将运行张力增大至6.5 kN、7.5 kN后,正馈线垂向振幅分别降低43.3%和37.8%,正馈线水平振幅降低21.9%,保护线垂向振幅降低53.5%,保护线水平振幅分别降低46.2%和45.2%。对比不同运行张力下附加导线振幅可以得出,将两导线张力提高至6.5 kN、7.5 kN可大幅降低附加导线振幅。在实际线路设计时,可以通过使用滑轮补偿装置、棘轮补偿装置、弹簧补偿装置等增大导线运行张力,从而提高附加导线抗风性能。
4.4 阻尼比对附加导线舞动的影响阻尼比指阻尼系数与临界阻尼系数之比,表示结构体标准化的阻尼大小,以及导线对振动能量的消散能力。为分析接触网附加导线阻尼比对舞动幅值的影响,在模型中将档距设置为50 m,正馈线、保护线分别设置其初始张力,附加导线阻尼比分别设置为0.4%、0.5%、1.0%、1.5%、2.0%,得到不同阻尼比下附加导线舞动响应结果。不同阻尼比下正馈线振幅变化趋势见图 12(c)。从图 12(c)可以看出,随阻尼比增大,正馈线及保护线振幅整体明显降低,将阻尼比增大至1.5%、2.0%后,正馈线垂向振幅分别降低40.5%和47.6%,正馈线水平振幅分别降低13.8%、19.4%,保护线垂向振幅分别降低41.1%、43.8%,保护线水平振幅分别降低18.0%、21.9%。对比不同导线阻尼比下附加导线振幅可以得出,其他线路参数不变时,提高导线阻尼比至1.5%及以上可以有效消耗导线从外界环境吸收的能量,从而降低两线的舞动幅值。在实际线路设计时,可以在接触网附加导线上安装阻尼器或阻尼间隔棒等来增大导线阻尼比。
4.5 导线悬挂点处最大动张力分析接触网附加导线舞动时的大幅运动会对导线线夹、连接金具以及绝缘子产生较大的动态冲击载荷,过大的冲击载荷将直接威胁接触网系统的结构安全。本文以最大动张力系数(最大动张力与运行张力的比值)来分析附加导线舞动产生的动态冲击载荷对接触网附加导线的影响。分别设置不同档距(35 m、40 m、45 m、50 m、55 m),不同运行张力(初始张力、4 500 N、5 500 N、6 500 N、7 500 N),不同阻尼比(0.4%、0.5%、1.0%、1.5%、2.0%),分析对导线悬挂点最大动张力系数的影响。
图 13为导线悬挂点最大动张力系数随档距、运行张力及阻尼比变化曲线。由图 13(a)可以看出,正馈线悬挂点最大动张力系数随档距增加呈现增大趋势,保护线悬挂点最大动张力系数在35~50 m档距变化相对稳定,基本低于1.5,但在55 m档距下动张力系数明显增大。由图 13(b)可以看出,正馈线及保护线悬挂点最大动张力系数均随运行张力增大呈现先增大后减小趋势,运行张力为5.5 kN,最大动张力系数存在最大值。由图 13(c)可以看出,正馈线悬挂点最大动张力系数随导线阻尼比增加呈下降趋势,保护线悬挂点最大动张力系数在阻尼比0.05%之后变化相对稳定,基本低于1.21。通过分析可以得出,附加导线档距过大,运行张力及阻尼比过小容易引起导线悬挂点张力过大而导致的掉线、断线等事故。
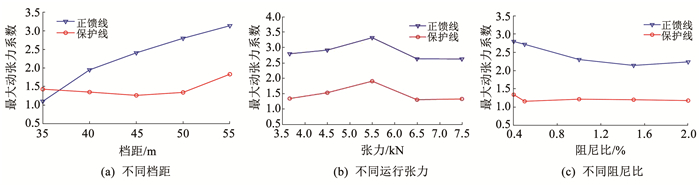
|
图 13 不同线路参数下附加导线最大动张力系数 Fig. 13 Maximum dynamic tension coefficient of additional conductors under different line parameters |
兰新高铁接触网附加导线中正馈线电压为27.5 kV,主要起到防电磁干扰及减少电能损耗等作用。保护线接地,主要起保护跳闸、防雷等作用。正馈线和保护线都处于田野侧,且悬挂点水平距离仅为1.5 m,垂直距离仅为1.6 m。由于两导线距离较近以及舞动存在非同期性,线间最小空气间隙可能不满足安全距离要求,而导致线间放电跳闸故障。接触网附加导线发生非同期舞动的主要原因如下:
1) 由于路基以及挡风墙对来流的影响,使得挡风墙后正馈线和保护线气动系数以及其位置处风速、风攻角出现明显差异,导致两导线所受气动荷载不同;
2) 正馈线及保护线不为同一型号,如截面积、单位质量、弹性模量等不同;
3) 正馈线和保护线在相同环境温度下的张力及弧垂不同。
图 14为接触网附加导线舞动线间距离示意,由于附加导线主要发生单半波舞动,仅取档距中点处舞动位移进行分析即可,线间安全距离判据式为:
| $ D_{a b}-\left(a_i+b_i\right)<D_m $ | (7) |
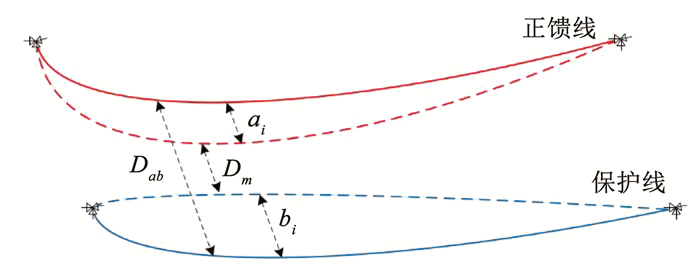
|
图 14 接触网附加导线舞动线间距离示意 Fig. 14 Schematic of distance between galloping additional conductors of OCS |
式中: Dab为正馈线和保护线在自重状态下的最小距离;ai和bi分别为正馈线和保护线的舞动位移;Dm为线间安全距离,根据TB 10621—2014《高速铁路设计规范》[20],安全距离取300 mm。
5.2 附加导线的线间最小距离影响因素分析正馈线与保护线舞动过程中周期和相位对于导线间距离有着十分重要的影响。以15 m/s风速为例,附加导线设置为档距50 m,初始张力,阻尼比0.4%,计算附加导线垂向位移对比曲线见图 15。从图中可以看出,正馈线及保护线垂向位移响应存在明显相位差,这也是造成线间距离变化的主要原因。根据正馈线和保护线档距中点处舞动位移曲线并结合悬挂点位置及弧垂高度,并通过距离公式便可求得任一时刻的线间距离。附加导线线间距离时程曲线见图 16,可见15 m/s风速下50 m档距附加导线线间动态距离约在0.79~3.29 m之间,大于线间安全距离。

|
图 15 附加导线垂向位移时程曲线 Fig. 15 Time history curves of vertical displacement of additional conductors |

|
图 16 附加导线线间距离时程曲线 Fig. 16 Time history curves of distance between additional conductors |
为明确线路参数对导线线间最小距离的影响,在10~25 m/s风速下,分别设置不同档距(35 m、40 m、45 m、50 m、55 m),不同张力(初始张力、4 500 N、5 500 N、6 500 N、7 500 N),不同阻尼比(0.4%、0.5%、1.0%、1.5%、2.0%),分析线间最小距离的变化规律。正馈线和保护线的线间最小距离与档距、运行张力及阻尼比的关系见图 17。通过图 17可以看出,随档距减小、附加导线运行张力及阻尼比增大,线间最小距离呈递增趋势。不同线路参数下(档距、运行张力及阻尼比)附加导线舞动时线间最小距离均随风速增大出现减小趋势,当风速高于20 m/s时,大档距、低运行张力、低阻尼比附加导线舞动时线间最小距离低于安全距离300 mm。因此在20~25 m/s风速下,将档距缩短至35 m、40 m,运行张力增大至6.5 kN、7.5 kN,阻尼比提高至1.5%、2.0%,线间最小距离可以达到设计要求。
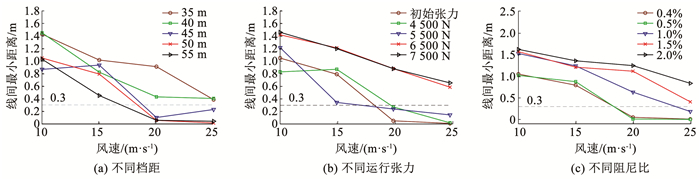
|
图 17 不同线路参数下附加导线舞动时线间最小距离 Fig. 17 Minimum distance between lines during galloping of additional conductors under different line structure parameters |
1) 35 m和40 m档距对导线在不同风速下的舞动均有明显的抑制效果,50 m和55 m档距对大风区段线路的安全运行最为不利。将导线运行张力提高至6.5 kN,正馈线垂向及水平振幅分别降低37.8%和21.9%,保护线垂向及水平振幅分别降低53.5%和45.2%。改变导线阻尼比可以使得正馈线及保护线振幅出现明显的变化,提高导线阻尼比至1.5%及以上能有效降低两线的舞动幅值。
2) 正馈线悬挂点最大动张力系数随档距增加呈现增大趋势,保护线悬挂点最大动张力系数在35~50 m档距变化相对稳定,基本低于1.5。正馈线及保护线悬挂点最大动张力系数均随运行张力增加呈现先增大后减小趋势。正馈线悬挂点最大动张力系数随导线阻尼比增加呈下降趋势,保护线悬挂点最大动张力系数在阻尼比0.5%之后变化相对稳定,基本低于1.21。附加导线档距过大,运行张力及阻尼比过小容易引起导线悬挂点张力过大而导致的掉线、断线等事故。
3) 档距减小时,导线运行张力及阻尼比均增大,附加导线舞动周期及侧向刚度变大,线间最小距离呈增大趋势。不同线路参数下(档距、运行张力及阻尼比)附加导线舞动时线间最小距离均随风速增大出现减小趋势。当风速高于20 m/s时,40 m以上档距、6.5 kN及以下运行张力、1.5%及以下阻尼比,附加导线舞动时线间最小距离低于线间安全距离300 mm。
4) 进行大风区段接触网附加导线设计应尽量选取小档距。为提高抗风性能,可加装滑轮、棘轮、弹簧补偿装置等来增大导线运行张力。在附加导线上加装阻尼器或阻尼间隔棒等以增大导线阻尼比。结合施工条件和经济效益,档距选择40 m,导线运行张力设置6.5 kN,导线阻尼比选择设置1.5%可有效减少因附加导线舞动及线间距不足引起的连接金具磨损、掉线、线间放电跳闸等事故。
| [1] |
王争鸣. 兰新高铁穿越大风区线路选线及防风措施设计[J]. 铁道工程学报, 2015, 32(1): 1. WANG Zhengming. Route selection and wind protection measures design of Lanzhou Xinjiang high speed railway crossing gale area[J]. Journal of Railway Engineering, 2015, 32(1): 1. |
| [2] |
黄双林. 兰新高铁防风标准研究[J]. 铁道工程学报, 2019, 36(6): 14. HUANG Shuanglin. Research on the wind break standard of Lanzhou-Urumqi High-Speed Railway[J]. Journal of Railway Engineering Society, 2019, 36(6): 14. |
| [3] |
张友鹏, 张永丰, 赵珊鹏, 等. 大风区接触网低风压正馈线设计及防舞有效性分析[J]. 铁道科学与工程学报, 2022, 19(12): 3494. ZHANG Youpeng, ZHANG Yongfeng, ZHAO Shanpeng, et al. Design and analysis on anti-galloping effectiveness of low wind pressure AF wire of overhead catenary system in gale zone[J]. Journal of Railway Science and Engineering, 2022, 19(12): 3494. |
| [4] |
赵珊鹏, 张永丰, 张友鹏, 等. 兰新高铁大风区低风压正馈线受力特性[J]. 西南交通大学学报, 2023, 58(5): 1154. ZHAO Shanpeng, ZHANG Yongfeng, ZHANG Youpeng, et al. Mechanical characteristics of low-wind-pressure catenary positive feeder in gale area of Lanzhou-Urumuqi high-speed railway[J]. Journal of Southwest Jiaotong University, 2023, 58(5): 1154. |
| [5] |
张友鹏, 王鹏, 赵珊鹏, 等. 大风区段接触网多跨距正馈线舞动特性[J]. 高电压技术, 2022, 48(9): 3612. ZHAO Shanpeng, WANG Peng, ZHANG Youpeng, et al. Galloping characteristics of catenary multi-span positive feeder in gale area[J]. High Voltage Engineering, 2022, 48(9): 3612. |
| [6] |
赵珊鹏, 张海喜, 张友鹏, 等. 基于流固耦合的大风区接触网正馈线舞动机制分析[J]. 哈尔滨工业大学学报, 2023, 55(10): 130. ZHAO Shanpeng, ZHANG Haixi, ZHANG Youpeng, et al. Analysis of the galloping mechanism of the positive feeder of the overhead contact system in windy areas based on fluid structure coupling[J]. Journal of Harbin Institute of Technology, 2023, 55(10): 130. |
| [7] |
BELLOLI M, MELZI S, NEGRINI S, et al. Numerical analysis of the dynamic response of a 5-conductor expanded bundle subjected to turbulent wind[J]. IEEE Transactions on Power Delivery, 2010, 25(4): 3105. DOI:10.1109/TPWRD.2010.2056396 |
| [8] |
楼文娟, 余江, 姜雄, 等. 覆冰导线三自由度耦合舞动稳定性判定及气动阻尼研究[J]. 土木工程学报, 2017, 50(2): 55. LOU Wenjuan, YU Jiang, JIANG Xiong, et al. Determination of three degree of freedom coupled galloping stability and aerodynamic damping of iced conductor[J]. Journal of Civil Engineering, 2017, 50(2): 55. |
| [9] |
MUHAMMAD B W, TAKASHI I, MUHAMMAD W S. Galloping response prediction of ice-accreted transmission lines[C]//4th Advances in Wind and Structures. Seoul: [s. n. ], 2008: 876
|
| [10] |
刘小会, 韩勇, 陈世民, 等. 连续档覆冰导线舞动数值模拟及参数分析[J]. 力学与实践, 2014, 36(1): 37. LIU Xiaohui, HAN Yong, CHEN Shimin, et al. Numerical simulation and parameter analysis of galloping of continuous iced conductor[J]. Mechanics and Practice, 2014, 36(1): 37. |
| [11] |
蔡萌琦, 严波, 吕欣, 等. 覆冰四分裂导线空气动力系数数值模拟[J]. 振动与冲击, 2013, 32(5): 132. CAI Mengqi, YAN Bo, LV Xin, et al. Numerical simulation of aerodynamic coefficient of iced four bundle conductor[J]. Vibration and Shock, 2013, 32(5): 132. |
| [12] |
胡霁, 董彦武, 文志科, 等. 1 000 kV交流紧凑型输电线路舞动计算分析[J]. 高电压技术, 2011, 37(8): 1862. HU Ji, DONG Yanwu, WEN Zhike, et al. Galloping calculation and analysis of 1000kV AC compact transmission line[J]. High Voltage Technology, 2011, 37(8): 1862. |
| [13] |
赵莉, 严波, 蔡萌琦, 等. 连续档覆冰四分裂导线舞动特征数值模拟研究[J]. 应用数学和力学, 2014, 35(5): 487. ZHAO Li, YAN Bo, CAI Mengqi, et al. Numerical simulation of galloping characteristics of continuous iced four bundle conductor[J]. Applied Mathematics and Mechanics, 2014, 35(5): 487. |
| [14] |
李旭亮, 霍冰, 刘习军. 匀减速风场下覆冰导线舞动的数值模拟研究[J]. 应用力学学报, 2021, 38(2): 700. LI Xuliang, HUO Bing, LIU Xijun. Numerical simulation of galloping of iced conductor under uniform deceleration wind field[J]. Journal of applied mechanics, 2021, 38(2): 700. |
| [15] |
赵珊鹏, 岳永文, 张友鹏. 挡风墙尾流作用下导线表面粗糙度对接触网正馈线气动特性的影响[J]. 重庆大学学报, 2023, 46(1): 46. ZHAO Shanpeng, YUE Yongwen, ZHANG Youpeng. The influence of wire surface roughness on the aerodynamic characteristics of the catenary positive feeder under the action of the wake flow of the wind-break wall[J]. Journal of Chongqing University, 2023, 46(1): 46. |
| [16] |
CAI M, YANG X, ZHOU L, et al. Numerical investigation on galloping of iced quad bundle conductors[J]. IEEE Transactions on Power Delivery, 2012, 27(2): 784. DOI:10.1109/TPWRD.2012.2185252 |
| [17] |
DIANA G, MANENTI A, MELZI S. Energy method to compute the maximum amplitudes of oscillation due to galloping of iced bundled conductors[J]. IEEE Transactions on Power Delivery, 2021, 36(5): 2804. DOI:10.1109/TPWRD.2020.3027157 |
| [18] |
赵珊鹏, 葛威, 王思华, 等. 兰新高铁大风区段接触网附加导线新型三角防舞器有效性分析[J]. 高电压技术, 2022, 48(12): 4852. ZHAO Shanpeng, GE Wei, WANG Sihua, et al. Effectiveness analysis of new triangle anti-galloping device for OCS additional conductors in strong wind section of Lanzhou-Xinjiang High-Speed Railway[J]. High Voltage Engineering, 2022, 48(12): 4852. |
| [19] |
王圣昆. 大风区接触网状态分析及在线监测研究[D]. 北京: 北京交通大学, 2018 WANG Shengkun. Research on catenary status analysis and on-line monitoring in strong wind area[D]. Beijing: Beijing Jiaotong University, 2018 |
| [20] |
国家铁路局. 高速铁路设计规范: TB 10621—2014[S]. 北京: 中国铁道出版社, 2014: 136 State Railway Administration. Code for design of high speed railway TB 10621—2014[S]. Beijing: China Railway Press, 2014: 136 |
 2024, Vol. 56
2024, Vol. 56


