2. 北京交通大学 土木建筑工程学院,北京 100044;
3. 中交隧道工程局有限公司,北京 100088
2. School of Civil Engineering, Beijing Jiaotong University, Beijing 100044, China;
3. CCCC Tunnel Engineering Bureau Co., Ltd, Beijing 100088, China
盘形滚刀破岩性能优异,在盾构和全断面岩石掘进机(tunneling boring machine, TBM)中被广泛的用作破岩刀具[1-4]。然而,滚刀磨损问题严重影响掘进效率,降低工程效益。滚刀磨损主要可分为正常磨损(均磨)和非正常磨损(刀圈断裂、偏磨等)两大类[5-6]。深圳某TBM地铁隧道在1 592 m的掘进距离内,有高达871把滚刀因过量磨损而更换,其中87%的滚刀是由于正常磨损而更换,其余则是由于非正常磨损而更换[7]。广州地铁某盾构区间在上软下硬地层中掘进时,由于地层分界面处刀圈受到剧烈的冲击荷载作用,刀圈崩坏十分频繁[8]。杭州地铁三号线在复合地层中仅掘进30 m,大量边缘滚刀已出现刀圈断裂和脱落现象,且由于刀盘泥饼导致滚刀启动扭矩变大无法自转,刀具普遍存在偏磨现象[9]。
国内外学者对滚刀磨损问题开展了大量研究。在滚刀正常磨损方面,文献[10]推导了基于密实核理论的滚刀磨损速率预测模型。文献[11]以磨粒磨损机理为基础建立了TBM正面滚刀寿命预测模型。文献[12]开展了干燥、水和海水等不同环境条件下的滚刀磨损实验。文献[13]以水和空气为冷却介质进行了刀圈和岩石之间的磨损实验。文献[14]建立了一种考虑能量转换和推力分布不均匀的圆盘铣刀磨损预测模型。文献[15]基于PFC2D方法,进行了单滚刀、双滚刀和三滚刀作用下复合岩体破碎过程的模拟。文献[16]采用颗粒流方法建立了盘形滚刀与含平行双节理岩体的二维数值模型,研究了节理特征对盘形滚刀破岩的影响。文献[17]建立了多滚刀三维破岩离散元模型,发现在滚刀旋转破岩过程中,滚刀会对两侧的岩石施加横向压缩,从而促进裂纹扩展和穿透。文献[18]针对临空面条件下滚刀破岩机理问题,采用离散元方法开展了临空面辅助滚刀破岩的数值模拟研究。文献[19]采用FDM-DEM耦合方法,对不同刀间距和贯入度条件下双滚刀破岩进行仿真。文献[20]采用MatDEM软件构建了滚刀破岩大尺寸三维模型,计算分析了刀间距与贯入度之比对滚刀破岩比能的影响,最终得到了使得破岩比能最小的最优刀间距与贯入度之比。文献[21]采用EDEM对不同滚刀刃角、刃宽和贯入度工况下滚刀磨损进行了分析。在滚刀非正常磨损方面,文献[22]采用线弹性断裂力学分析了不同因素对滚刀刀座失效概率的影响。文献[23]基于刀圈的成形、加工、损伤、失效等全寿命周期阶段,分析了各因素对刀圈性能的影响。文献[24]基于自制冲击-滑动(冲滑)复合磨损试验机分析了刀盘与地层之间的相对刚度对滚刀的磨损行为的影响。文献[25]建立了滚刀切削复合地层的有限元模型动力分析模型,分析了不同贯入度、切削速度条件下滚刀的冲击荷载响应。文献[26]基于RBD-DEM耦合方法,分析了滚刀在软硬不均地层中贯入角度的变化对其所受冲击荷载的影响。文献[27]利用MatDEM软件建立了圆盘切割机切割岩石的三维离散元模型,模拟了岩石在冲击载荷作用下的破碎。文献[28]建立了一系列有限元模型,认为随着穿透深度的增加,刀环断裂的风险急剧增加,窄刀环在土-岩界面的断裂破坏可能性较高。文献[29]基于PFC3D方法,建立了盘形滚刀切削复合地层的数值模型,分析了盘形刀受力和岩石裂纹扩展,认为软岩地层中滚刀滚动力的降低将导致滚刀偏磨。文献[30]基于RBD-DEM耦合方法,采用自定义计算程序实现了盘形刀具与地层的相互作用,对滚刀与岩体之间的滑移机理进行了研究。文献[31]提出了一种基于能量分析的滚刀偏磨深度预测方法。文献[32]开展了滚刀在滚动、滑动和不同偏磨量状态下切割岩石的室内实验,分析了刀具与岩石的接触行为和受力变化。
综上所述,目前对滚刀磨损的研究主要集中在正常磨损和诱发刀圈断裂的冲击荷载等方面,盘形滚刀的偏磨与刀具的运动状态密切相关,但对这一问题的深入研究还较少,且现有研究均为滚刀对岩体进行线性切割[18-21, 26-27],与滚刀真实运动状态存在差异。本文基于离散单元法,建立了考虑滚刀自转和绕刀盘公转的滚动圆周切割模型,对滑移状态下滚刀破岩的三向受力和磨损进行了对比分析,并结合工程实例中刀具磨损统计数据对数值仿真结果进行了验证,相关结论可为实际工程中通过掘进参数变化判断刀具是否发生偏磨提供依据。
1 滚动圆周切割模型 1.1 接触模型选取 1.1.1 Hertz-Mindlin (no slip)接触模型Hertz-Mindlin (no slip)模型用于描述颗粒与颗粒或者颗粒与刀具之间的相互作用,见图 1。
|
图 1 颗粒之间相互作用示意 Fig. 1 Interaction between particles |
颗粒之间法向力Fn、切向力Ft和力矩Ti为:
| $ F_{\mathrm{n}}=4 / 3 E^* \sqrt{R^*} \delta_{\mathrm{n}}^{3 / 2} $ | (1) |
| $ F_{\mathrm{t}}=-S_t \delta_{\mathrm{t}} $ | (2) |
| $ T_{\mathrm{i}}=-\mu_{\mathrm{r}} F_{\mathrm{n}} R_{\mathrm{L}} \omega_{\mathrm{i}} $ | (3) |
式中:E*为颗粒等效弹性模量, R*为颗粒的等效半径, δn为颗粒间的法向重叠量,St为颗粒间切向刚度,μr为颗粒间滚动摩擦系数,RL为颗粒接触点到颗粒质心的距离, ωi为颗粒在接触点处的单位角速度向量。
颗粒等效弹性模量E*、等效半径R*、等效质量m*与等效剪切模量G*满足:
| $ \frac{1}{E^*}=\frac{1-\mu_i^2}{E_i}+\frac{1-\mu_j^2}{E_j} $ | (4) |
| $ \frac{1}{R^*}=\frac{1}{R_i}+\frac{1}{R_j} $ | (5) |
| $ \frac{1}{m^*}=\frac{1}{m_i}+\frac{1}{m_j} $ | (6) |
| $ \frac{1}{G^*}=\frac{1}{G_i}+\frac{1}{G_j} $ | (7) |
式中:Ei、Ej、μi、μj、Ri、Rj、mi、mj、Gi、Gj分别代表颗粒i和颗粒j的弹性模量、泊松比、半径、质量和剪切模量。
颗粒间法向刚度Sn与切向刚度St为:
| $ S_{\mathrm{n}}=2 E^* \sqrt{R^* \delta_{\mathrm{n}}} $ | (8) |
| $ S_{\mathrm{t}}=8 G^* \sqrt{R^* \delta_{\mathrm{n}}} $ | (9) |
颗粒间法向阻尼力Fnd和切向阻尼力Ftd为:
| $ F_{\mathrm{n}}^{\mathrm{d}} =-2 \sqrt{5 / 6} \beta \sqrt{S_{\mathrm{n}} m^*} \boldsymbol{v}_{\mathrm{n}}^{\text {ret }} $ | (10) |
| $ F_{\mathrm{t}}^{\mathrm{d}} =-2 \sqrt{5 / 6} \beta \sqrt{S_{\mathrm{t}} m^*} \boldsymbol{v}_{\mathrm{t}}^{\text {ret }} $ | (11) |
式中:vnret为颗粒间相对速度的法向分量,vtret为颗粒间相对速度的切向分量,e是恢复系数,β是与恢复系数相关的参数,可由下式计算:
| $ \beta=\frac{\ln e}{\sqrt{\ln ^2 e+{\rm{ \mathsf{ π}}}^2}} $ | (12) |
Hertz-Mindlin with Bonding模型被广泛用于模拟岩石破碎,颗粒之间通过黏结键进行连接,在黏结后,颗粒之间的Hertz-Mindlin(no slip)接触模型失效,随后对每个时间步长Δt内黏结键的力δFn、δFt和力矩δMn、δMt进行迭代:
| $ \delta F_{\mathrm{n}} =-v_{\mathrm{n}} S_{\mathrm{N}} A \Delta t $ | (13) |
| $ \delta F_{\mathrm{t}} =-v_{\mathrm{t}} S_{\mathrm{T}} A \Delta t $ | (14) |
| $ \delta M_{\mathrm{n}} =-\omega_{\mathrm{n}} S_{\mathrm{T}} J \Delta t $ | (15) |
| $ \delta M_{\mathrm{t}} =\frac{-\omega_{\mathrm{t}} S_{\mathrm{T}} J \Delta t}{2} $ | (16) |
其中:
| $ A={\rm{ \mathsf{ π}}} R_{\mathrm{B}}^2 $ | (17) |
| $ J={\rm{ \mathsf{ π}}} R_{\mathrm{B}}^4 / 2 $ | (18) |
式中:RB为黏结键的半径大小, Δt为时间步长, vn为颗粒的法向速度, vt为颗粒的切向速度, wn为法向角速度, wt为切向角速度。当法向和切向的应力值超过设定的黏结键参数最大值时,黏结键发生断裂,其判定如下:
| $ \sigma_{\text {max }} <-F_{\mathrm{n}} / A+2 M_{\mathrm{t}} R_{\mathrm{B}} / J $ | (19) |
| $ \tau_{\text {max }} <-F_{\mathrm{t}} / A+M_{\mathrm{n}} R_{\mathrm{B}} / J $ | (20) |
对于几何体刀具磨损的模拟,采用Archard Wear模型[7],磨损量计算如下:
| $ \mathrm{d} h=K v \sigma \mathrm{d} t / H $ | (21) |
式中:h为研究材料的磨损深度; σ为两种材料法向应力; A为材料间的接触面积; v为两种材料的相对运动速度; t为运动时间; H为研究材料的硬度情况,K为两种材料相对磨损系数,在此对滚刀磨损进行定性分析,取K=10-5。
1.2 参数标定综合考虑滚刀磨损模型的大小、计算机性能和计算精度等因素,最终确定颗粒半径大小为2 mm。单轴压缩岩石试样由3 574个半径2 mm的颗粒黏结在一起组成,单轴压缩仿真中应力-应变曲线和黏结键断裂数目见图 2,峰值抗压强度达71 MPa时,上压板压力骤降,大量黏结键瞬间发生断裂,岩石发生破坏。巴西劈裂仿真中黏结键参数与单轴压缩试验中取值相同,整个试样由893个颗粒黏结在一起,试件破坏过程中应力-应变曲线和黏结键断裂数目见图 3,试件峰值强度达到7.9 MPa时,大量黏结键瞬间发生断裂,岩石试件发生劈裂破坏。黏结参数由试错法标定获得,结合文献[16-20],多次调整黏结参数,使得岩石单轴压缩和巴西劈裂破坏形态与室内实验破坏形态相似。颗粒黏结参数取值见表 1,刀圈与颗粒材料参数取值见表 2。

|
图 2 单轴压缩应力-应变曲线 Fig. 2 Stress - strain curve of uniaxial compression |

|
图 3 巴西劈裂应力-应变曲线 Fig. 3 Stress - strain curve of Brazilian splitting |
| 表 1 材料黏结微观参数 Tab. 1 Microscale parameters of material bonding |
| 表 2 颗粒与刀圈材料参数 Tab. 2 Material parameters of particles and disc cutters |
滚刀模型选取为当前比较常用的18英寸常截面盘形滚刀,刃宽18 mm,半径216 mm。综合考虑计算速度和滚刀破岩影响范围,仅对滚刀刀圈部分进行建模,建立沿圆周径向长234 mm、高150 mm、对应圆心角为20°的岩石模型,模型由252 054个颗粒组成,岩石与滚刀接触面为临空面,其余5个边界采用wall单元进行约束,设定滚刀以角速度ω绕刀盘中心轴转动的同时以角速度ω1绕其刀轴自转,模型建立过程见图 4。

|
图 4 模型建立过程 Fig. 4 Modeling process |
滚刀的安装半径被设定为R=1 000 mm,进行圆周切割,见图 5。当滚刀与岩石之间不产生滑移时,刀圈运动满足如下公式:
| $ \omega R=\omega_1 R_1 $ | (22) |

|
图 5 圆周切割模型 Fig. 5 Cutting model with circle moving |
式中:ω为滚刀绕刀盘中心角速度,R为滚刀安装半径,ω1为滚刀绕刀轴转动角速度,R1为滚刀半径。
为探究滚刀滑移状态对破岩垂直力和滚动力的影响,定义滑移率参数η,用于定量描述滚刀滑移状态:
| $ \eta=1-\frac{\omega_2}{\omega_1} $ | (23) |
式中: ω2为滚刀破岩时的实际自转角速度,ω1为滚刀做完全滚动运动时的角速度,则η可用于定量描述滚刀与岩体之间滑移程度,当η=0时,为滚刀与岩体之间无滑移,滚刀处于滚动破岩状态,当η=1时,滚刀与岩体之间为完全滑移接触,滚刀处于滑动破岩状态。当η介于0~1之间时,用于描述滚刀与岩体之间处于一种在滑动与滚动之间来回切换的状态。本文在仿真时设定刀盘转速ω1为7 r/min,贯入度H为5 mm,4种不同滑移状态下的滑移率分别为0(滚动破岩)、0.3、0.7、1(滑动破岩)。
2 计算结果分析 2.1 模型合理性验证CSM模型[33]综合考虑了岩石材料的抗压强度、抗拉强度以及滚刀的结构参数,常用于常截面盘形滚刀荷载计算的,且已被大量工程实测数据验证,在此采用CSM模型计算结果与本文数值仿真结果进行对比,相互验证,CSM模型中:
| $ F_{\mathrm{V}}=C_0 \frac{\varphi R_0 T}{1+\psi}\left[\frac{S \boldsymbol{\sigma}_{\mathrm{c}}^2 \boldsymbol{\sigma}_{\mathrm{t}}^2}{\varphi \sqrt{\boldsymbol{R}_0 T}}\right]^{1 / 3} \cos (\varphi / 2) $ | (24) |
| $ F_{\mathrm{R}}=C_0 \frac{\varphi R_0 T}{1+\psi}\left[\frac{S \boldsymbol{\sigma}_{\mathrm{c}}^2 \boldsymbol{\sigma}_{\mathrm{t}}^2}{\varphi \sqrt{\boldsymbol{R}_0 T}}\right]^{1 / 3} \sin (\varphi / 2) $ | (25) |
式中:C0为无量纲常数,通常取2.12;T为刀刃宽度(m),本文为18 mm;ψ为刀刃压力分布系数,介于-0.2~0.2之间,由刀刃形状决定,在此取为-0.2;S为刀间距(m),本文为单滚刀破岩,在此取刀间距为较大值200 mm;σc为岩石单轴抗压强度(Pa);σt为岩石抗剪强度(Pa); φ为滚刀与岩石接触角,由贯入度H(m)和滚刀半径R0(m)计算:
| $ \varphi=\arccos \frac{R_0-H}{R_0} $ | (26) |
图 6为仿真计算结果与CSM模型计算结果对比,数值仿真中垂直力FV和滚动力FR处于一种波动变化的状态。在0°~5°范围内,滚刀与岩体接触面积逐渐增加,破岩力逐渐变大,此时岩体内无裂纹扩展,故垂直力FV初始瞬间峰值较大。在5°~15°破岩过程中,由于岩石裂纹扩展的存在,垂直力FV明显变小,不断波动。在15°~20°范围内,刀圈与岩体逐渐分离,破岩力衰减为0。CSM模型计算垂直力FV为184.4 kN,滚动力FR为19.9 kN,在5°~15°范围内,仿真结果在CSM模型计算值附近上下波动,垂直力FV略低于理论值,滚动力FR吻合效果较好,本文模型计算滚刀破岩力基本合理。

|
图 6 仿真结果与CSM模型计算结果对比 Fig. 6 Comparison between simulation and CSM model calculation results |
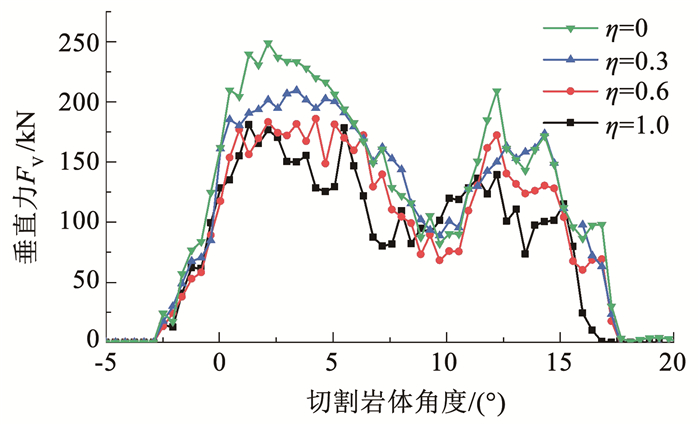
图 7为不同滑移率η条件下滚刀垂直力FV,当η=0、滚刀在滚动状态下破岩时,垂直力FV最大,在150 kN附近波动,且波动幅度较大,随着滚刀滑移率η的增加,垂直力FV呈现轻微减小的趋势,当η=1、滚刀在滑动状态下破岩时,垂直力FV最小,在120 kN左右,且整体波动幅度较小。图 8为不同滑移率η条件下滚刀滚动力FR,当η=0、滚刀在滚动状态下破岩时,滚动力FR最小,在20 kN附近波动,随着滚刀滑移率η的增加,滚动力FR呈现明显变大的趋势,当η=1、滚刀在滑动状态下破岩时,滚动力FR最大,在45 kN附近波动。
|
图 7 不同滑移率η条件下垂直力FV Fig. 7 Vertical force FV under different slip ratios η |

|
图 8 不同滑移率η条件下滚动力FR Fig. 8 Rolling force FR under different slip ratios η |
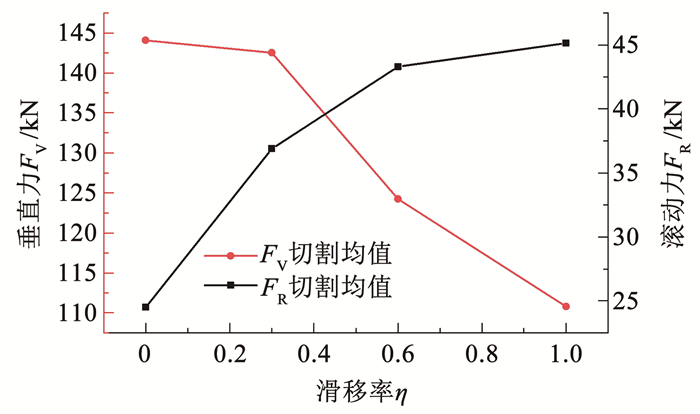
图 9为滚刀切割5°~15°岩体时FV和FR均值随滑移率η变化趋势,从滚动破岩到滑动破岩,垂直力FV均值由144 kN降低到110 kN,降低幅度为23.6%,滚动力FR均值由24.5 kN增加到45 kN,增幅达83.7%。分析原因认为,当滚刀由滚动破岩变为滑动破岩时,破岩机理发生改变,此时沿滚动力FR方向的切槽破岩作用会更加突出,沿垂直力FV方向的切深破岩作用则变弱,由此导致FR均值显著变大,FV均值略微减小。
|
图 9 切割均值随滑移率η变化趋势 Fig. 9 Variation trend of cutting mean with slip ratio η |
图 10为不同滑移率下滚刀磨损云图,滚刀以滚动状态破岩时,刀圈磨损沿刀圈径向较为均匀的分布,此时滚刀发生均磨。滚刀以滑动状态破岩时,在滚刀与岩石接触的局部位置发生严重磨损,造成滚刀偏磨。实际工程中可通过滚刀垂直力和滚动力的变化趋势分析滚刀状态,及时判断滚刀是否发生偏磨。

|
图 10 不同滑移率η条件下的磨损云图 Fig. 10 Wear nephogram under different slip ratios η |
单把滚刀垂直力FV累加可得到刀盘部分推力Fc,单把滚刀滚动力FR的力矩累加可得到刀盘部分扭矩Tc,其满足:
| $ F_{\mathrm{c}} =\sum\limits_1^N F_{\mathrm{V} N} $ | (27) |
| $ T_{\mathrm{c}} =\sum\limits_1^N F_{\mathrm{R} N} R_N $ | (28) |
式中:N为刀盘上滚刀个数,FVN、FRN、RN分别为第N把滚刀的垂直力、滚动力和安装半径。因此,单把滚刀从滚动破岩转变为滑动破岩时FV和FR的变化,可通过刀盘上大量滚刀处于偏磨状态时扭矩和推力的变化反映出来。
3.1 工程地质北京市南水北调团九二期二标区间隧道单洞全长1 712 m,采用1台开挖直径为6.29 m的泥水气压平衡式盾构施工,该工程地质条件复杂多变,盾构始发后自西南向东北方向掘进,先后穿越大粒径砂卵石地层、全断面硬岩地层、上软下硬地层和黏土地层。区间隧道最大纵坡坡度为21‰,最大埋深42.5 m,最小平面曲线半径为350 m,区间隧道纵剖面见图 11。

|
图 11 区间隧道地质纵断面 Fig. 11 Geological profile of section tunnel |
在盾构掘进过程中,刀具磨损十分严重,尤其在全断面硬岩地层中,换刀十分频繁。每次开仓后对刀具进行检查,滚刀磨损状态主要分为四大类:正常磨损(磨损量少于15 mm)、正常磨损(磨损量大于15 mm)、偏磨、刀圈或刀齿断裂,对磨损量超过15 mm的滚刀和其他非正常磨损滚刀进行更换后继续掘进。现场典型的磨损刀具见图 12。

|
图 12 现场典型磨损刀具 Fig. 12 Typical worn disc cutters on site |
以1220~1280环掘进过程实测数据为例,对刀盘上大量滚刀处于正常磨损状态下破岩掘进参数变化进行分析。由图 13可知,自1238环始,推力从1 200 kN左右上升到2 200 kN,刀盘扭矩无明显变化,在1256环开仓对刀具进行检查,刀具磨损情况见图 14,29把滚刀磨损量小于15 mm,占比69.05%,5把滚刀磨损量大于15 mm,占比11.9%,5把滚刀处于偏磨状态,占比11.9%。开仓换刀后,推力缓慢下降,扭矩无明显变化。由此可见,当刀盘上大量滚刀以正常滚动状态破岩时,随着刀具正常磨损加剧,三参主要表现为推力变大,扭矩无明显变化。由于长时间停机、边缘滚刀磨损导致刀盘切削半径变小等因素,换刀后刀盘推力下降存在约10环滞后(盾体长10.5 m,管片环宽1.2 m),为定量分析推力增幅,取开仓换刀前3环为刀具严重磨损状态,换刀掘进10环之后的3环为刀具正常状态,掘进参数增幅Z为
| $ Z=\frac{X_{i-1}-X_i}{X_i} $ | (29) |

|
图 13 1220到1290环掘进参数变化 Fig. 13 Parameter changes of 1220 to 1290 ring |

|
图 14 1256环开仓后刀具磨损情况 Fig. 14 Disc cutter wear when opening in 1256 ring |
式中,Xi为开仓换刀后掘进第11~13环的参数均值,Xi-1开仓前3环参数均值,由式(25)计算得此工况下推力增幅约为41.6%。分析原因认为,伴随着滚刀正常磨损的发生,刀刃形状发生改变,滚刀刃宽和刃角都变大,单把滚刀破岩垂直力变大,由此导致盾构推力变大,单把滚刀受到的滚动力主要由其启动扭矩决定,滚刀正常磨损对启动扭矩并无影响,因此正常磨损状态下刀盘扭矩将无明显变化。
3.3.2 滚刀以偏磨为主以1055~1090环和1280~1320环掘进过程实测数据为例,对刀盘上大量滚刀处于偏磨状态下掘进参数变化进行分析。图 15为1055~1090环掘进过程中掘进参数变化趋势,自1065环始,扭矩从1 500 kN·m上升到2 500 kN·m左右,推力无明显变化,在1075环开仓对刀具进行检查,刀具磨损情况如图 16所示,2把滚刀磨损量大于15 mm,占比4.76%,12把滚刀处于偏磨状态,占比28.57%。开仓换刀后,扭矩迅速下降至正常水平,推力无明显变化,由式(29)计算得此工况下扭矩增幅高达261.51%。

|
图 15 1055到1090环掘进参数变化 Fig. 15 Parameter changes of 1055 to 1090 ring |

|
图 16 1075环开仓后刀具磨损情况 Fig. 16 Disc cutter wear when opening in 1057 ring |
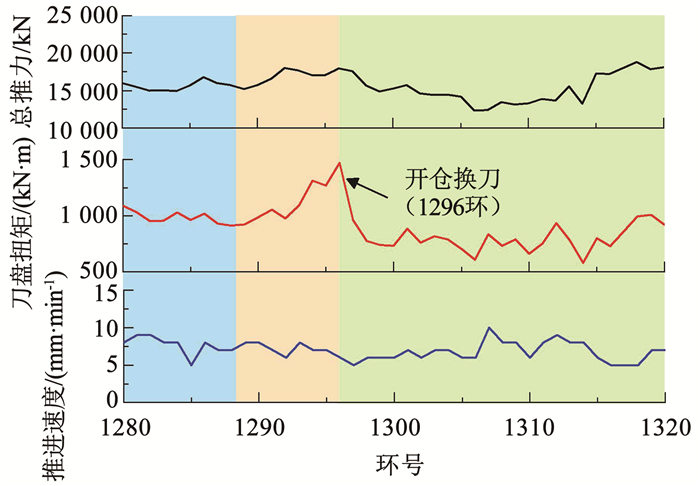
图 17为1280~1320环掘进过程中掘进参数变化趋势。自1280环始,扭矩从1 000 kN·m上升到1 500 kN·m左右,推力无明显变化,在1296环开仓对刀具进行检查,刀具磨损情况如图 18所示,3把滚刀磨损量大于15 mm,占比7.14%,8把滚刀处于偏磨状态,占比19.05%。开仓换刀后,扭矩迅速下降至正常水平,推力无明显变化,由式(29)计算得此工况下扭矩增幅约为55.85%。
|
图 17 1280到1320环掘进参数变化 Fig. 17 Parameter changes of 1280 to 1320 ring |

|
图 18 1290环开仓后刀具磨损情况 Fig. 18 Disc cutter wear when opening in 1290 ring |
综合分析两次开仓情况,偏磨滚刀占比19.05%,扭矩增幅55.85%,偏磨滚刀占比28.57%,扭矩增幅261.51%,可见刀盘上大量滚刀以滑动状态破岩时,刀盘扭矩剧烈增加。分析原因认为,当滚刀以滑动状态破岩时,滚刀不再自转,此时单把滚刀破岩滚动力会变大,当刀盘上的大量滚刀处于滑动状态时,则表现为扭矩持续增加,大量滚刀发生偏磨,这与本文数值仿真结论表现出一致性。
3.3.3 滚刀正常磨损和偏磨同时发生以1110~1180环掘进过程实测数据为例,对刀盘上滚刀正常磨损和偏磨占比均较高时三参动态变化进行分析。由图 19可知,自1128环始,推力由1 300 kN上升到1 900 kN左右,扭矩由700 kN·m上升到约1 200 kN·m,在1296环开仓对刀具进行检查,刀具磨损情况如图 20所示,6把滚刀磨损量大于15 mm,占比14.29%,9把滚刀处于偏磨状态,占比21.43%。开仓换刀后,推力缓慢下降,扭矩均迅速下降至正常水平。由式29计算得此工况下推力增幅约为36.57%,扭矩增幅约为80.89%。

|
图 19 1110到1180环掘进参数变化 Fig. 19 Parameter changes of 1110 to 1180 ring |

|
图 20 1151环开仓后刀具磨损情况 Fig. 20 Disc cutter wear when opening in 1151 ring |
综合4次换刀结果来看,刀盘上大量滚刀处于正常磨损状态时,主要表现为推力增大。大量滚刀处于偏磨状态时,主要表现为扭矩增大,其中偏磨滚刀占比19.05%和28.57%时,扭矩增幅分别为55.85%和261.51%。正常磨损和偏磨均大量存在时,表现为扭矩推力同步增大,其中偏磨滚刀占比21.43%时,扭矩增幅为80.89%。在本文案例中,大量滚刀发生偏磨时仅表现为扭矩逐渐增大,推力无明显变化,并未出现本文数值仿真中单滚刀滑动破岩时垂直力降低的现象,分析原因认为是由于刀盘上正常磨损滚刀导致的推力增大与偏磨滚刀导致的推力降低存在相互抵消。
4 结论基于离散单元法,建立了同时考虑滚刀自转和绕刀盘公转的滚动圆周切割模型,定义了一个滑移率参数η用于描述滚刀的滑移状态,对不同滑移率η条件下滚刀破岩受力和磨损进行了分析,并结合工程实例进行验证,主要结论如下:
1) 数值仿真中垂直力FV和滚动力FR在CSM模型计算值附近上下波动,两者较为吻合,表明了本文模型的合理性。
2) 数值仿真结果表明,随着滑移率η的增大,垂直力FV呈轻微减小趋势,滚动力FR明显变大,从滚动破岩到滑动破岩,垂直力FV降幅为23.6%,滚动力FR增幅达83.7%,滑动破岩将导致滚刀偏磨。
3) 工程实测数据表明,刀盘上大量滚刀处于正常磨损状态时,主要表现为推力增大。大量滚刀处于偏磨状态时,主要表现为扭矩增大,其中偏磨滚刀占比19.05%和28.57%时,扭矩增幅分别为55.85%和261.51%。正常磨损和偏磨均大量存在时,表现为扭矩推力同步增大,其中偏磨滚刀占比21.43%时,扭矩增幅为80.89%。
4) 数值仿真和实测数据表现出较高的一致性。综合4次开仓换刀结果,可将刀盘扭矩增幅超过50%作为判定大量滚刀发生偏磨的重要依据。
| [1] |
JIN Dalong, YUANG Dajun, LI Xinggao, et al. Probabilistic analysis of the disc cutter failure during TBM tunneling in hard rock[J]. Tunnelling and Underground Space Technology, 2021, 109: 103744. DOI:10.1016/j.tust.2020.103744 |
| [2] |
LI Xingchun, LI Xinggao, YUANG Dajun. Application of an interval wear analysis method to cutting tools used in tunneling shields in soft ground[J]. Wear, 2017, 392: 21. DOI:10.1016/j.wear.2017.09.010 |
| [3] |
REN Dongjie, SHEN Shuilong, ARULRAJAH A, et al. Prediction model of TBM disc cutter wear during tunnelling in heterogeneous ground[J]. Rock Mechanics and Rock Engineering, 2018, 51(11): 3599. DOI:10.1007/s00603-018-1549-3 |
| [4] |
MASSOUD B, JAFAR K H. A case study on TBM tunnelling in fault zones and lessons learned from ground improvement[J]. Tunnelling and Underground Space Technology, 2017, 63: 162. DOI:10.1016/j.tust.2016.12.006 |
| [5] |
FARROKH E, KIM D Y. A discussion on hard rock TBM cutter wear and cutterhead intervention interval length evaluation[J]. Tunnelling and Underground Space Technology, 2018, 81: 336. DOI:10.1016/j.tust.2018.07.017 |
| [6] |
LIN Laikuang, MAO Qingsong, XIA Yimin, et al. Experimental study of specific matching characteristics of tunnel boring machine cutter ring properties and rock[J]. Wear, 2017, 378: 1. DOI:10.1016/j.wear.2017.01.072 |
| [7] |
SU Weiling, LI Xinggao, JIN Dalong, et al. Analysis and prediction of TBM disc cutter wear when tunneling in hard rock strata: a case study of a metro tunnel excavation in Shenzhen, China[J]. Wear, 2020, 446: 203190. DOI:10.1016/j.wear.2020.203190 |
| [8] |
张伟森. 上软下硬地层盾构机滚刀磨损特性研究[J]. 地下空间与工程学报, 2019, 15(2): 583. ZHANG Weisen. Characteristics of disc cutter failures in mixed-face ground condition[J]. Chinese Journal of Underground Space and Engineering, 2019, 15(2): 583. |
| [9] |
李强, 甘鹏路. 复合地层盾构刀具磨损控制技术研究[J]. 现代隧道技术, 2020, 57(1): 168. LI Qiang, GAN Penglu. On cutter wearing control technology of the shield passing through mixed strata[J]. Modearn Tunneling Technology, 2020, 57(1): 168. |
| [10] |
佘磊, 张社荣, 和孙文, 等. 基于密实核理论的TBM盘形滚刀磨损预测模型研究[J]. 岩土工程学报, 2022, 44(5): 970. YU Lei, ZHANG Sherong, SUN Wen, et al. Prediction model for TBM disc cutter wear based on dense core theory[J]. Chinese Journal of Geotechnical Engineering, 2022, 44(5): 970. |
| [11] |
乔世范, 王超, 刘志新, 等. 基于磨粒磨损机理的全断面隧道掘进机滚刀寿命预测[J]. 吉林大学学报(工学版), 2020, 50(6): 2068. QIAO Shifan, WANG Chao, LIU Zhixing, et al. Life prediction of tunnel boring machine abrasive wear mechanism[J]. Journal of Jilin University (Engineering and Technology Edition), 2020, 50(6): 2068. |
| [12] |
ZHANG Xuhui, XIA Yimin, ZHANG Yichao, et al. Experimental study on wear behaviors of TBM disc cutter ring under drying, water and seawater conditions[J]. Wear, 2017, 392-393: 109. DOI:10.1016/j.wear.2017.09.020 |
| [13] |
FU Jie, ZENG Guiying, ZHANG Hao, et al. Experimental investigation on wear behaviors of TBM disc cutter ring with different cooling methods[J]. Engineering Failure Analysis, 2022, 134: 106076. DOI:10.1016/j.engfailanal.2022.106076 |
| [14] |
SHEN Xiang, CHEN Xiangsheng, FU Yanbin, et al. Prediction and analysis of slurry shield TBM disc cutter wear and its application in cutter change time[J]. Wear, 2022, 498-499: 204314. DOI:10.1016/j.wear.2022.204314 |
| [15] |
蒋明镜, 傅程, 王华宁, 等. 简单复合岩体中TBM多滚刀破岩机理离散元分析[J]. 土木工程学报, 2019, 52(Sup.1): 120. JIANG Mingjing, FU Cheng, WANG Huaning, et al. Distinct element analysis of mechanism of rock fragmentation induced by TBM cutting in simply composite rock mass with multiple cutters[J]. China Civil Engineering Journal, 2019, 52(Sup.1): 120. |
| [16] |
施雪松, 管清正, 王文扬, 等. 双节理岩体TBM滚刀破岩过程数值模拟[J]. 山东大学学报(工学版), 2020, 50(4): 70. SHI Xuesong, GUAN Qingzheng, WANG Wenyang, et al. Numerical simulation of rock fragmentation process by TBM cutterin double-joint rock mass[J]. Journal of Shandong University (Engineering Science), 2020, 50(4): 70. DOI:10.6040/j.issn.1672-3961.0.2019.744 |
| [17] |
LI Tao, ZHANG Zhongyu, JIA Chengtao, et al. Investigating the cutting force of disc cutter in multi-cutter rotary cutting of sandstone: simulations and experiments[J]. International Journal of Rock Mechanics and Mining Sciences, 2022, 152: 105069. DOI:10.1016/j.ijrmms.2022.105069 |
| [18] |
汪珂. 临空面辅助滚刀破岩的数值模拟研究[J]. 铁道工程学报, 2020, 37(10): 96. WANG Ke. Numerical Simulation research on the rock fracturing by a TBM disc cutter assisted by free faces[J]. Journal of Railway Engineering Society, 2020, 37(10): 96. |
| [19] |
徐琛, 刘晓丽, 王恩志, 等. 基于耦合FDM-DEM方法的TBM滚刀最优化研究[J]. 土木工程学报, 2020, 53(Sup.1): 286. XU Chen, LIU Xiaoli, WANG Enzhi, et al. Optimal conditions for TBM disc cutter rock fragmentation based on FDM-DEM method[J]. China Civil Engineering Journal, 2020, 53(Sup.1): 286. DOI:10.15951/j.tmgcxb.2020.s1.045 |
| [20] |
薛亚东, 周杰, 赵丰, 等. 基于MatDEM的TBM滚刀破岩机理研究[J]. 岩土力学, 2020, 41(Sup.1): 337. XUE Yadong, ZHOU Jie, ZHAO Feng, et al. Rock breaking mechanism of TBM cutter based on MatDEM[J]. Rock and Soil Mechanics, 2020, 41(Sup.1): 337. DOI:10.16285/j.rsm.2019.1656 |
| [21] |
AGRAWAL A K, CHATTOPADHYAYA S, MURTHY V M S R. Delineation of cutter force and cutter wear in different edge configurations of disc cutters——An analysis using discrete element method[J]. Engineering Failure Analysis, 2021, 129: 105727. DOI:10.1016/j.engfailanal.2021.105727 |
| [22] |
马捷, 曲传咏. TBM刀座焊缝疲劳可靠性分析[J]. 机械科学与技术, 2020, 39(8): 1149. MA Jie, QU Chuanyong. Analysis of fatigue reliability of cutter saddle weld for tBM[J]. Mechanical Science and Technology for Aerospace Engineering, 2020, 39(8): 1149. DOI:10.13433/j.cnki.1003-8728.20190269 |
| [23] |
王好平, 张蒙祺, 莫继良. 盾构/TBM滚刀刀圈性能强化研究现状[J]. 材料导报, 2022, 36(7): 49. WANG Haoping, ZHANG Mengqi, MO Jiliang. Current status on performance enhancement of shield machine/TBM cutter ring[J]. Materials Reports, 2022, 36(7): 49. |
| [24] |
孙瑞雪, 段文军, 牟松, 等. 盾构滚刀刀圈材料的冲滑复合磨损性能研究[J]. 摩擦学学报, 2022, 42(2): 314. SUN Ruixue, DUAN Wenjun, MOU Song, et al. The study on impact-sliding composite wear properties of shield cutter ring material[J]. Tribology, 2022, 42(2): 314. DOI:10.16078/j.tribology.2021012 |
| [25] |
孙佳程, 廖少明, 孙连勇, 等. 土岩复合地层盾构滚刀冲击荷载及振动响应分析[J]. 现代隧道技术, 2020, 57(5): 167. SUN Jiacheng, LIAO Shaoming, SUN Lianyong, et al. Analysis of impact load and vibration response of shield disc cutters in soil-rock composite strata[J]. Modearn Tunneling Technolong, 2020, 57(5): 167. DOI:10.13807/j.cnki.mtt.2020.05.021 |
| [26] |
徐公允, 徐汪豪, 姚志刚, 等. 基于三维RBD-DEM耦合方法的贯入角度对滚刀冲击影响分析[J]. 现代隧道技术, 2021, 58(6): 77. XU Gongyun, XU Wanghao, YAO Zhigang, et al. analysis on influence of penetration angle on disc cutter impact based on three-dimensional RBD-DEM coupling method[J]. Modearn Tunneling Technolong, 2021, 58(6): 77. DOI:10.13807/j.cnki.mtt.2021.06.009 |
| [27] |
XUE Yadong, ZHOU Jie, LIU Chun, et al. Rock fragmentation induced by a TBM disc-cutter considering the effects of joints: a numerical simulation by DEM[J]. Computers and Geotechnics, 2021, 136: 104230. DOI:10.1016/j.compgeo.2021.104230 |
| [28] |
LING Xianzhang, KONG Xiangxun, TANG Liang, et al. Preliminary identification of potential failure modes of a disc cutter in soil-rock compound strata: interaction analysis and case verification[J]. Engineering Failure Analysis, 2022, 131: 105907. DOI:10.1016/j.engfailanal.2021.105907 |
| [29] |
ZHANG Zhiqiang, ZHANG Kangjian, DONG Weijie, et al. Study of rock-cutting process by disc cutters in mixed ground based on three-dimensional particle flow model[J]. Rock Mechanics and Rock Engineering, 2020, 53(8): 3485. DOI:10.1007/s00603-020-02118-y |
| [30] |
FANG Yong, YAO Zhigang, XU Wanghao, et al. The performance of TBM disc cutter in soft strata: A numerical simulation using the three-dimensional RBD-DEM coupled method[J]. Engineering Failure Analysis, 2021, 119: 104996. DOI:10.1016/j.engfailanal.2020.104996 |
| [31] |
YANG Haiqing, LIU Bolong, WANG Yanqing, et al. Prediction model for normal and flat wear of disc cutters[J]. International Journal of Geomechanics, 2021, 21(3). DOI:10.1061/(ASCE)GM.1943-5622.0001950 |
| [32] |
SUN Ruixue, MO Jiliang, ZHANG Mengqi, et al. Cutting performance and contact behavior of partial-wear TBM disc cutters: a laboratory scale investigation[J]. Engineering Failure Analysis, 2022, 137: 106253. DOI:10.1016/j.engfailanal.2022.106253 |
| [33] |
李彬嘉, 晏启祥, 黄杰, 等. 基于CSM模型的盾构机滚刀受力及磨损规律[J]. 中国铁道科学, 2020, 41(6): 91 LI Binjia, YAN Qixiang, HUANG Jie, et al. Mechanical characteristics and wear laws of disc cutters of shield machine based on CSM model[J]. China Railway Science, 41(6): 91 |
 2024, Vol. 56
2024, Vol. 56


