脉冲位置调制(pulse position modulation, PPM)[1]凭借其功率效率高、抗干扰能力强等优点,在无线通信及光通信系统中得到广泛应用。可当该调制信号在信道中传输时,会受到多普勒频移效应[2]的干扰,同时发射端和接收端的时间基准信号存在频率偏差,这给接收端的正确解调带来极大挑战。因此,调制信号需要进行同步[3-4],并消除频偏。在传统的数字同步方案中,文献[5]通过在基带信号的频谱中插入导频信号,然后在接收端获取该定时信号的方式实现位同步,但该方法需要额外占用频带资源;在文献[6]中,通过数字锁相环,产生一个高频时钟,其时钟周期的大小决定了本地时钟的调节步长,因此其频率往往为PPM符号的数十至数百倍,通过比较PPM符号和本地时钟的相位,逐步调整本地时钟相位,使二者相位对齐,最终完成位同步。但该方法需要锁相环产生更高频的时钟,这对于高速PPM符号而言,其成本和功耗代价是系统实现时所无法承受的。
基于上述原因,本文提出了一种新型PPM符号调制方法,并通过在模拟域对高速PPM符号进行频偏补偿和数据解调。该方法通过对接收数据进行初始相位追踪,频偏信息提取,瞬时相位补偿3个步骤消除接收数据与本地时钟的初始相位差,并实现符号同步和频偏纠正,最后通过解调器使补偿后的同步时钟对接收到的符号进行数据解调。最终,在40 nm CMOS工艺下,对该方法的电路进行设计、仿真和验证。实验结果表明,在工艺、电压和温度process voltage temperature, PVT)变化时,该方法均能实现良好的频偏补偿效果,并能正确解调数据。
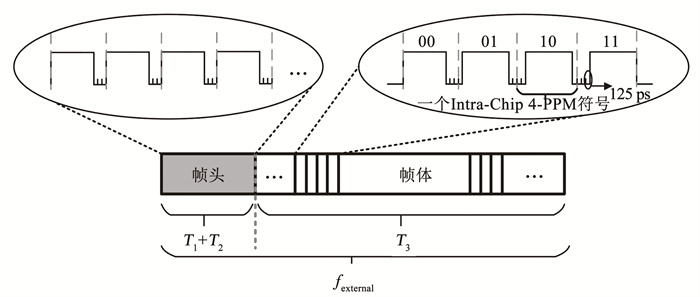
1 频偏补偿环路及数据解调设计 1.1 码片内4-PPM符号与整体系统架构本文的数据帧结构见图 1,一帧数据由帧头和帧体构成,本文用fexternal表示。帧体的长度会远远大于帧头。这种帧结构结合本文提出的新型PPM符号,其工作过程如下:在帧头位置,即T1+T2时段,是包含发射端时钟信息的帧头符号,其特点是帧头符号脉冲在每个符号周期中的起始位置始终保持不变;在帧体位置,即T3时段,是发射端调制后的PPM符号信息,该调制符号利用符号脉冲宽度小于符号周期的特点,令符号脉冲的起始位置随着输入数据信息变化在符号周期内产生变化。这种PPM符号有别于传统的PPM符号:1)传统的PPM符号是将一个符号周期划分成多个码片,符号脉冲的宽度等于码片宽度,脉冲位置的变化体现为脉冲整体出现在不同的码片位置,但是脉冲位置在码片内不发生变化,因此我们可以把传统的PPM符号称为码片间PPM(Inter-Chip PPM)符号;2)本文提出了一种新型PPM符号,这种符号不再将其周期划分为多个码片,而是视作一个完整的码片,同时将符号脉冲宽度设定为小于符号周期,这样符号脉冲可以通过在一个符号周期内的起始位置的变化来表征输入数据的调制信息。因为该调制方法的脉冲位置变化体现在一个码片周期内(也就是一个符号周期内),因此可以称作码片内PPM符号。例如符号脉冲宽度为1.6 ns,符号周期为2 ns,这样符号脉冲的起始位置可以在400 ps范围内变化,并以此位置的变化来表征输入数据所含信息。Intra-Chip PPM调制的特点,使其特别适用于高速PPM符号调制系统,并且在频谱效率和功耗效率方面都相对于传统的Inter-Chip PPM,有着明显的优势。
本文设计的电路与系统是针对符号速率为500 MHz的高速PPM符号调制解调系统。在传统的Inter-Chip 4-PPM符号中,只有一个宽度为500 ps的码片为高电平,其占据了约2 GHz带宽。在对调制符号所占带宽与数据解调难易程度进行折中考虑后,本文提出的Intra-Chip 4-PPM符号将一个符号周期(码片周期)分成16个时隙,每个时隙125 ps,使其13个时隙都为高电平,其只占据约615 MHz的带宽。Intra-Chip 4-PPM符号与2位二进制数的映射关系,如图 1右上角所示。
|
图 1 本文所提出的数据帧结构及Intra-Chip 4-PPM符号 Fig. 1 Proposed structure of data frame and Intra-Chip 4-PPM symbol |
整个电路由以下几个部分组成:延迟锁定环(delay locked loop, DLL)、相位插值器(phase interpolator, PI)、相位检测(phase detector, PD)、数字锁定探测器(digital lock detector, DLD)、顶层状态机(top finite state machine, TFSM)、解调器(demodulator)等。其中PI又由相位选择(phase selector, PS)、相位插值核(PI core)、电流舵式数模转换器(current steer digital-to-analog converter, CS-DAC)和双转单电路(differential to single-ended, D-to-S)构成。图 2中的锁相环(phase locked loop, PLL)为DLL和TFSM提供参考输入时钟。

|
图 2 本文所提出的频率补偿原理 Fig. 2 Proposed principle of frequency offset compensation |
整个环路的基本工作原理如下:由PLL产生的参考时钟fref输入至DLL中,DLL会产生32个同频等相差的时钟,分别为fphase1, fphase2, …, fphase32。根据TFSM的返回值,PS会从这些时钟中选出两对相邻的差分时钟,作为PI核的输入信号,同时CS-DAC分配电流权重,得到插值输出信号flocal。PD会依据flocal和fexternal上升沿的相位关系,在输出端产生高低电平。若flocal超前fexternal,则输出PD_early为1且PD_late为0;反之,若flocal滞后fexternal,则输出PD_early为0,PD_late为1。TFSM会根据PD的输出值,产生相应的DAC_code<4∶ 0>,使得整个环路构成负反馈。当该值要溢出时,TFSM会改变Section_code<4∶ 0>,使得flocal的相位能够连续变化,并且在负反馈环路的作用下flocal会实时追踪fexternal的相位,保持对齐。由于频偏的存在,所以环路是一个动态变化的过程,本文通过DLD来衡量环路是否动态锁定。在多个参考时钟周期内,每一次上升沿来临时,DLD会对PD的输出进行采样,并分别统计PD_early和PD_late为1的个数,然后将两者做差,其绝对值若小于设定的阈值,即判定动态锁定。
1.2 频偏补偿算法实现由图 3(b)所示,本文的频偏补偿时序分为以下3个步骤:

|
图 3 顶层状态机算法实现及频偏补偿时序 Fig. 3 Implementation of TFSM algorithm and timing of frequency offset compensation |
1) 在T1起始时刻,接收机收到的是来自发送端的数据帧头,该帧头包含的脉冲在一个Intra-Chip 4-PPM符号中的起始位置是固定不变的,即为时钟信号。该信号与本地时钟不仅存在频偏,而且存在初始相位差。所以在这一段时间内,TFSM会根据这两个信号的相位信息,实时调整本地时钟的相位,最终在T1末尾时刻,两者相位对齐,DLD产生锁定标志位送给TFSM。
2) 在T2时段,接收机接收到仍然是来自发送端的数据帧头,但此时初始相位差已经通过步骤1完成消除,因此TFSM可以通过记录DAC_code<4∶ 0>和Section_code<4∶ 0>的变化量,得到由频偏所产生的累积相移量,从而提取得到接收数据帧头与本地时钟的频偏信息。在这段时间内,反馈环路仍然正常工作,所以两者相位始终保持动态对齐。
3) 在T3时段,接收机收到的是来自发送端的数据帧体,该帧体的符号数据为脉冲起始位置随调制信息变化的Intra-Chip 4-PPM信号,TFSM会根据在T2时段提取的频偏信息,并通过TFSM和PI来改变本地时钟的瞬时相位,纠正频偏,以确保数据的正确解调。
图 3(a)中为T1至T3时段TFSM的具体实现原理,其中T2_code<15∶ 0>和T3_code<15∶ 0>均是可编程的16位2进制码,前者定义了T′ 2时段的持续时间,后者定义了T3时段的持续时间。
在T1末尾时刻,DLD锁定,DLD_lock变为1,此信号会送给T2_Counter,并做其使能信号,启动计数,通过计数来控制T′2时长,若计数值大于T2_code<15∶ 0>,则该计数器停止计数且T2_reach输出为1,并将此信号输入至Phase_Control以及Divider。Phase_Control会根据DLD_lock和T2_reach这2个指示信号的跳变情况,统计T′2时段内Early和Late为1的数量,并求出二者的差值,用T2_acc_code<15∶ 0>表示;该差值等于DAC_code<4∶ 0>的变化量,而该变化量即为本地时钟在T′2时间段内为了与数据帧头同步而产生的相位变化量,因此提取了该时段由频偏所引起的相移量。在T′2末尾时刻,T2_acc_code<15∶ 0>的值会输入到Divider,并作为除数。Divider的另一端输入为T2_code<15∶ 0>,表示被除数。Divider的除法功能是通过移位实现的,对于16位的2进制输入,需要16个输入参考时钟,才能完成除法功能。完成后,Divider_reach变为1,并将其输出的商和余数(均为16位2进制数)送给T3_Counter。Divider工作时段对应图 3(b)中的ΔT2部分,该模块的功能可描述为
| $ \frac{\left.T_2^{\prime} \text { 时段参考时钟周期数 ( T2_code }<15: 0>\right)}{T_2^{\prime} \text { 时段 PI 变化步长数 }(\text { T2_acc_code }<15: 0>)}=\\ 商…余数 $ | (1) |
式中商及余数表示要使PI中DAC_code<4∶ 0>变化一次所需的参考时钟周期数。通常情况下,周期数为大于1的小数。此外,本地时钟与接收数据的频偏可能为正也可能为负,所以在T′2时段会通过TFSM来判断频偏极性,并产生标志位Pole_flag,同样也送给T3_Counter。至此,T2时段结束。
当Divider_reach变为1后,送给Phase_Control的Early和Late信号,不是由PD产生,而是由T3_Counter所产生。若Pole_flag值为1,则T3_Counter的Early输出是脉宽为一个参考时钟周期的脉冲信号,Late输出恒为0;若Pole_flag值为0,则反之。2个脉冲信号的间隔,表示多久需进行一次瞬时相位补偿,其间隔为Divider的商或商加1乘以参考时钟周期。两者出现的权重,取决于余数与除数的比值。此外,当进入T3时段,T3_Counter开始计数,当计数值超过T3_code<15∶ 0>时,计数停止,并且T3_reach变为1,该信号同时会重置T2_Counter和Phase_Control。至此,T3时段结束,完成了一帧数据与本地时钟的频偏补偿。当下一帧数据来临时,又会重复T1至T3的过程。
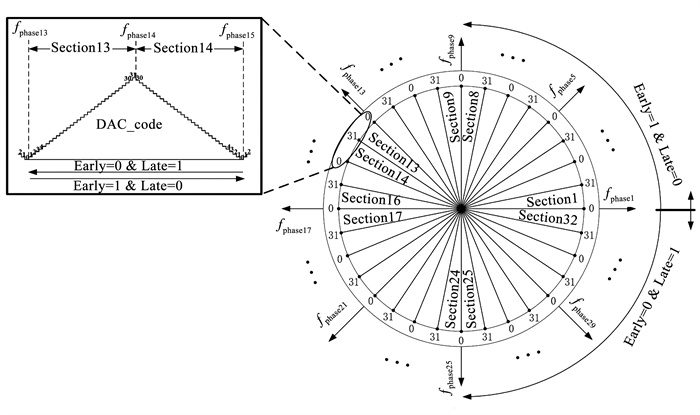
1.3 相位控制算法实现在本文中,本地时钟的相位调整区间有32个。DLL通过延迟线产生了32个时钟,相邻的两项时钟形成一个相位区间,fphase1与fphase32也构成一个区间,定义这些区间为Section1, Section2, …, Section32。在每个区间内,又将其分成32个步长,用DAC_code<4∶ 0>表示。其值变化,取决于当前采样Early和Late值的情况,若Early=1且Late=0,则DAC_code<4∶ 0>朝逆时针方向变化;若Early=0且Late=1,则DAC_code<4∶ 0>朝顺时针方向变化,见图 4。
|
图 4 区间及DAC码字跳变原理 Fig. 4 Phase sections and principle of DAC code hopping |
区间的交界处,代表DAC_code<4∶ 0>值即将溢出,需要区间切换。以Section13和Section14为例,当Section13中DAC_code<4∶ 0>加至31需要跳转到Section14时,传统做法会将DAC_code<4∶ 0>清零,并重新累加。这意味着,在区间的交界处,存在码字从“11111”直接跳变为“00000”的情况,这对于CS-DAC而言,会引入极大的电流毛刺,从而影响PI的插值结果。针对这一问题,本文在区间跳变时,使得DAC_code<4∶ 0>连续变化,见图 4左上部分。在Early=1且Late=0情况下,DAC_code<4∶ 0>在Section13是递增变化,在Section14递减变化,注意到在区间的交界处,只存在一个31,即DAC_code<4∶ 0>是从Section13的31跳变到Section14的30,同样在Section14和15的交界处,其值从Section14的0跳变到Section15的1,这一现象是由PI的插值特性所决定的,其原因将在后文中详细叙述。
2 电路设计与实现 2.1 PI电路设计与实现 2.1.1 PS设计PS的作用是从DLL产生的32相时钟中选出2对相邻的差分时钟信号,送给PI核进行相位插值。在区间跳变时,PS为了使插值得到的时钟相位能够连续变化,需要将相邻差分对位置对调,与DAC_code<4∶ 0>的连续变化相匹配,Section_code<4∶ 0>与输出时钟项对应关系见表 1。
| 表 1 相位选择器的输入码字与输出时钟项对应关系 Tab. 1 Relationship of input code and output clocks of phase selector |
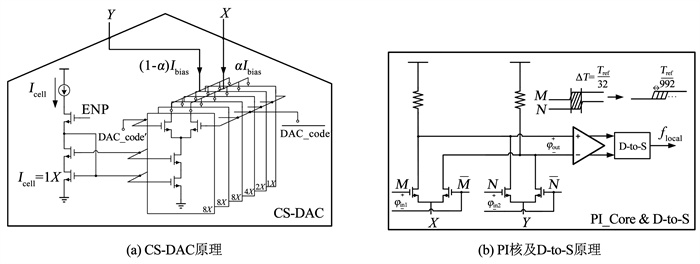
图 5(a)为CS-DAC的电路原理,其中镜像电流源均采用了共源共栅的NMOS架构,提高输出阻抗,确保电流镜像的准确度[7-8]。DAC中的参考电流为Icell,该电流会分别按比例成倍镜像给6个模块。每个模块均有一对差分NMOS管,DAC_code<4∶ 0>中的高2位解码成温度计码,与低3位二进制码一同送至差分对的栅极,从而控制每个模块电流流向。由此可以得到X和Y点的电流分别为αIbias,(1-α)Ibias,其中α介于0和1之间。Icell和Ibias的关系式为
| $ I_{\text {bias }}=31 * I_{\text {cell }} $ | (2) |
图 5(b)是PI核及D-to-S电路原理图,PI核中两对差分对的源端分别与DAC的输入端X、Y相连[9-10]。因此,流入两对差分对的电流大小取决于DAC如何分配两条支路的电流权重。两路尾电流经过相同尺寸的差分对,在同一电阻负载端进行叠加,形成输出电压。因此,PI的输出可以定义为相邻差分输入时钟的权重叠加。PI的输出瞬时相位与输入时钟相位的关系可表示为
| $ \varphi_{\text {out }}=\alpha \varphi_{\mathrm{in} 1}+(1-\alpha) \varphi_{\mathrm{in} 2} $ | (3) |
|
图 5 PI电路原理 Fig. 5 Schematic of phase interpolator |
PI插值的精度由DAC_code<4∶ 0>码字位数决定,两项相邻的输入时钟,可以得到32相插值输出。但在本文中,区间边界处会共用一个输入时钟,即前一个区间的M输入,仍做下一个区间的M输入,为了保证DAC_code<4∶ 0>的连续跳变,在边界处只存在一个“0”或者“31”,所以每个区间只有31个有效步长,32个区间一共992个步长,这对于500 MHz的参考时钟,可实现2.016 ps的调节步长。相较于文献[6],本文不仅不需要多倍的高频时钟,而且实现了更加精细的步长。遍历DAC_code<4∶ 0>, 可得区间1的32相插值输出时钟,见图 6。PI的线性度不仅与输出RC时间常数有关,而且与输入相位差ΔT也有关。在文献[11-13]中,ΔT取值均较小,通过减小ΔT/RC的值,可提高PI的线性度。因此,本文选取的ΔT为参考时钟周期的1/32,为62.5 ps,来保证较好的线性度。由图 7可见,在整个插值范围内,PI的DNL最大为0.502 LSB(least significant bit),即0.183°;INL最大为0.896 LSB,即0.325°。INL在每个区间的边界处,得到明显改善,这是由于DLL的校准作用。从系统层面而言,PI除了实现插值移相的功能;在T2时段,PI和TFSM还需要统计由频差所造成的相移量。所以,本文的PI及TFSM也实现了传统时间数字转换器(time-to-digital converter, TDC)的功能,并且其测量范围理论上为无穷大,分辨率为2.016 ps。因此,PI在本文中实现功能复用,节省TDC的面积和功耗,避免由TDC所产生的测量误差。

|
图 6 区间1的32相插值输出时钟波形 Fig. 6 Simulated waveforms with 32 interpolated clocks in Section 1 |

|
图 7 PI的差分非线性和积分非线性 Fig. 7 Dyferential nonlinearity and integral nonlinearity of PI |
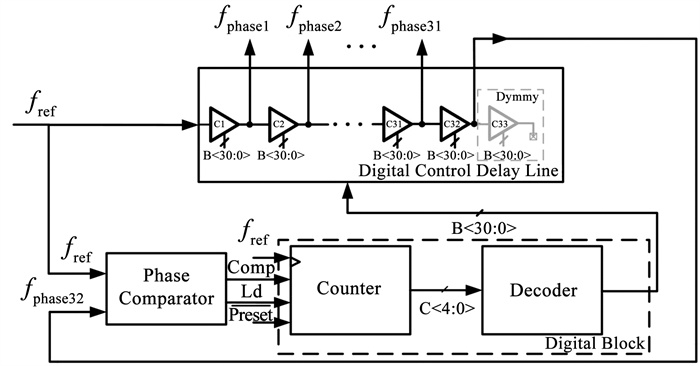
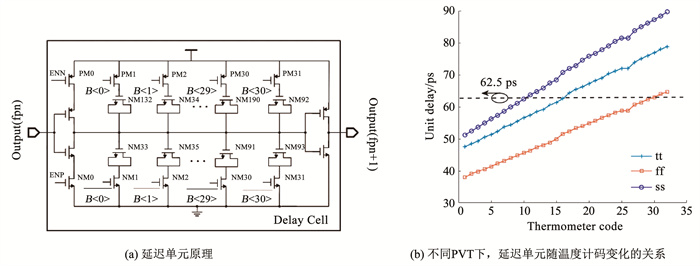
在T3时段,系统会消除flocal和fexternal的频偏,实现本地时钟与数据帧体的符号同步。并且,在这一时段,会利用完成频偏补偿的flocal对数据帧体进行实时解调。本文的解调器由DLL、采样触发器、解码器3部分构成, 见图 8(a)。flocal输入至DLL中,产生32相时钟,两两相差62.5 ps;取其中奇数项时钟(fphase1, fphase3, …, fphase32),作为每个触发器的采样时钟,则两两相差125 ps;触发器的另一端输入为Intra-Chip 4-PPM符号。由于符号与本地时钟的相位已经对齐,并且输入至触发器的采样时钟是奇数项,所以每相时钟对符号数据的采样点为符号中每个时隙(共16个时隙)的中间位置;每当flocal上升沿来临时,解码器会对16个采样值进行解码,最终输出一串2进制码流,完成解调,其各信号时序见图 8(b)。在图 9中,本文采用的DLL整体分为4个部分,分别是相位比较器(phase comparator,PC)[16]、数控延迟线(digital control delay line, DCDL)、计数器(counter)、解码器(decoder)[14]。DCDL由32个延迟单元所构成,延迟单元的电路结构[15]见图 10(a)。在延迟单元中,NM32-NM93构成了NMOS电容阵列,共31组。每组上下各一个,使得信号路径的充放电时间相匹配。每一组电容配有2个开关,控制电容接入还是接出,以此改变延迟。从图 10(b)可得,即使在PVT变化时,通过改变温度计码,单级延迟时间均能够覆盖62.5 ps。fphase32输入至PC与fref进行相位比较。计数器会根据PC的输出,进行加减C<4∶ 0>,而解码器将5位2进制数转换为31位温度计码,转换后的码字会同时控制每一级延迟单元中的开关阵列,从而调节DCDL的延迟,缩小fphase5与fref的相差,直至锁定。

|
图 8 解调器实现原理 Fig. 8 Principle of demodulator |
|
图 9 DLL架构 Fig. 9 Structure of DLL |
|
图 10 延迟单元的原理及PVT特性 Fig. 10 Schematic of delay cell and PVT characteristics |
本文的整体电路与系统是在Cadence公司旗下的Virtuoso软件平台,并基于UMC代工厂40 nm CMOS工艺库,进行设计、仿真和验证。诚然,本文的频偏补偿及数据解调的设计及实验是在码间串扰可被均衡器很好解决的前提下进行的。现设置本地时钟频率为500 MHz,接收数据与本地时钟的频率偏差度为50×10-6。频率偏差度可由下式计算:
| $ \Delta f=\frac{\left|f_{\mathrm{tx}}-f_{\mathrm{rx}}\right|}{f_{\mathrm{rx}}} * 100 \%=\frac{\left|T_{\mathrm{tx}}-T_{\mathrm{rx}}\right|}{T_{\mathrm{rx}}} \times 100 \% $ | (4) |
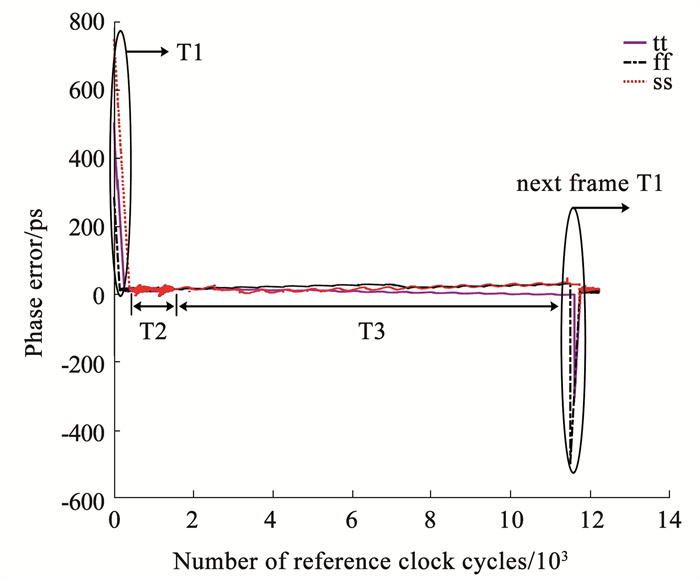
式中ftx、frx分别为接收数据的频率和本地时钟频率,而Ttx、Trx为与频率对应的单周期值。此外,T2_code<15∶ 0>赋值1 024,T3_code<15∶ 0>赋值10 240,表明T3约为T2的10倍。由于数据是Intra-Chip 4-PPM符号串,所以每个脉冲上升沿的来临时刻并不固定。为了更加直观地验证补偿效果,本文将接收数据从T2时刻进行时钟周期延拓,以此观察T1至T3时段中,外部时钟与本地时钟在每个周期内的相位差,从而得到在T3时段频偏的补偿效果,见图 11。同时,本文还对整体电路进行了PVT仿真,包括最快工艺角(ff,1.21 V,-40°)及最慢工艺角(ss,0.99 V,85°)。在T1截止时刻,数据帧与本地时钟的相位差并不为零,主要有2点原因。其一是由于PD模块采用CML(current mode logic)架构的D触发器,其在零点附近存在5 ps的判决盲区,无法判断数据帧与本地时钟的相位关系。其二是由于时钟存在随机抖动。在T3时段,若不进行频偏补偿,可由式(4)计算得到 Ttx-Trx 为0.1 ps,则这一时段所累积的相差将高达1 024 ps,这对数据解调而言,是致命的;而在本文的频偏补偿下,T3截止时刻,T1至T3时段累积的相差在典型,最快和最慢工艺角下,各减小至8.44 ps、30.93 ps和30.52 ps;若只考虑在T3时段累积的相差,则各为21.14 ps、17.25 ps、16.34 ps。因此,由式(5)可得:
| $ \text { 频偏补偿准确度 }=\frac{\text { 无补偿累积相差 }- \text { 补偿后累积相差 }}{\text { 无补偿累积相差 }} \times 100 \% $ | (5) |
|
图 11 累积相差随时间变化的关系 Fig. 11 Variation of phase error with time |
在上述3种工艺角下,本文的频偏补偿准确度分别为97.94%、98.32%、98.40%。由于频偏补偿是一个动态的过程,所以也可以用T3时段的平均频率偏差度来衡量补偿效果。对式(4)进一步拓展至式(6):
| $ \Delta f_{\mathrm{ave}}=\frac{\left|T_{\mathrm{tx}}^{\prime}-T_{\mathrm{rx}}^{\prime}\right|}{T_{\mathrm{rx}} \times N} \times 100 \%=\frac{\text { 补偿后累积相差 }}{T_{\mathrm{rx}} \times N} \times 100 \% $ | (6) |
式中:Δfave为平均频率偏差度;N为T3时段的参考周期数,此处N取值10 240;T′tx、T′rx分别为该时段接收数据的总周期值和补偿后本地时钟的总周期值。当Trx为2 ns时,可由式(6)计算得到典型工艺角下,T3时段补偿后的平均频率偏差度为1.03×10-6。
从算法层面而言,本文做到了无偏差补偿,但T3时段仍然累积了相差,造成这一现象主要有3个原因:第一个原因是PI本身存在非线性,其最大INL为0.896 LSB;其二是DLL锁定之后,PC的2个输入时钟存在微小的静态误差;其三是时钟的随机抖动。不过,对于本文PPM系统的数据正确解调而言,这些误差是系统所允许的。此外,T1、T2时段并不传输调制数据,可将这段时间看成数据帧的额外开销。其中T1时间长度不超过496(992/2)个参考周期,而T2、T3的时间段是可编程的,具有一定的自由度。所以当T2、T3的时间长度分别为512、20 480个参考周期时,此开销最多占数据帧长度的4.7%,然而从上文可知,这段开销是必要且有意义的。在T3时段,解调器对数据帧进行解调,其结果见图 12。本文电路的整体功耗为17.41 mW,各模块的功耗见表 2。与传统数字同步方案[6]相比,本文以较少的功耗代价,不仅对高速数据进行频偏补偿,实现符号同步,而且完成了数据解调。

|
图 12 Intra-Chip 4-PPM符号的解调结果 Fig. 12 Demodulation results of Intra-Chip 4-PPM symbols |
| 表 2 各子模块功耗 Tab. 2 Power consumption of sub-blocks |
针对接收端与反射端时钟存在频率偏移问题,设计并实现了一种模拟域频偏补偿的算法及电路,并对Intra-Chip 4-PPM符号进行同步解调,实现了1 Gbit/s的数据传输速率。通过T1时段相位追踪、T2时段频偏信息提取、T3时段频偏补偿3步实现了一帧数据与本地时钟的符号同步,并消除频偏。与传统的数字同步方案相比,本文改进了PPM符号,并且无需插入导频,节省频带资源;同时,在接收端也无需高频时钟数据恢复电路,减少资源开销。设计的TFSM模块使得CS-DAC的码字在区间跳变时连续变化,消除了由码字突变引起的电流毛刺,避免了PI输出的相位突变。DLL和PI的结合,使得PI在整个时钟周期内均可插值,实现插值的分辨率为2.016 ps,最大INL为0.325°。在T2时段,PI与TFSM的结合实现了TDC的功能,以此统计由频偏引起的累积相差。在T3时段,直接利用补偿后的本地时钟对数据进行解调。最终,本文通过实验证明,该电路的频偏补偿准确度达到了97.94%,并在各工艺角下,均具有良好的鲁棒性。该方法在无线通信和光通信的PPM数据同步及解调中具有良好的工程应用价值。
| [1] |
PIERCE J. Optical channels: practical limits with photon counting[J]. IEEE Transactions on Communications, 1978, 26(12): 1819. DOI:10.1109/TCOM.1978.1094043 |
| [2] |
华惊宇, 马章勇, 王东明, 等. 移动通信中一种精确的多普勒频移估计方法[J]. 电子与信息学报, 2005, 27(1): 95. HUA Jingyu, MA Zhangyong, WANG Dongming, et al. An accurate scheme for the Doppler shift estimation in mobile communication systems[J]. Journal of Electronics Information Technology, 2005, 27(1): 95. |
| [3] |
XIAO Yan, QIAN Wang, XIN Hao, et al. A high-efficiency multiplierless symbol synchronization algorithm for IEEE802.11x WLANs[J]. Wireless Personal Communications, 2017, 94(3): 1738. DOI:10.1007/s11277-016-3709-7 |
| [4] |
CHEN Ming, HE Jing, CAO Zizheng, et al. Symbol synchronization and sampling frequency synchronization techniques in real-time DDO-OFDM systems[J]. Optics Communications, 2014, 326: 80. DOI:10.1016/j.optcom.2014.04.011 |
| [5] |
WEN Miaowen, ZHENG Beixiong, GUAN Quansheng, et al. Novel pilot position detection for SC-FDE systems with frequency domain pilot multiplexing technique[J]. IEEE Signal Processing Letters, 2016, 23(7): 910. DOI:10.1109/LSP.2016.2564981 |
| [6] |
马爽, 吴志勇, 高世杰, 等. 改进的大气激光通信PPM调制解调系统设计[J]. 哈尔滨工业大学学报, 2016, 48(5): 105. MA Shuang, WU Zhiyong, GAO Shijie, et al. Design of modified atmospheric laser communication PPM modulation-demodulation system[J]. Journal of Harbin Institute of Technology, 2016, 48(5): 105. DOI:10.11918/j.issn.0367-6234.2016.05.017 |
| [7] |
GUPTA A, GUPTA L. Improved performance 6-bit 3.5 GS/s unary CS-DAC using glitch reduction[J]. International Journal of Electronics Letters, 2019, 8(6): 7. DOI:10.1080/21681724.2019.1625965 |
| [8] |
CHUNG S W, ABEDIASL H, HASHEMI H. A monolithically integrated large-scale optical phased array in silicon-on-insulator CMOS[J]. IEEE Journal of Solid-State Circuits, 2017(99): 12. DOI:10.1109/JSSC.2017.2757009 |
| [9] |
CHENG K H, HUNG C L, CHANG C H. A 0.77 ps RMS jitter 6-GHz spread-spectrum clock generator using a compensated phase-rotating technique[J]. IEEE Journal of Solid-State Circuits, 2011, 46(5): 1208. DOI:10.1109/JSSC.2011.2105690 |
| [10] |
YOON Y, PARK H, KIM C. A DLL-based quadrature clock generator with a 3-stage quad delay unit using the sub-range phase interpolator for low-jitter and high-phase accuracy DRAM applications[J]. IEEE Transactions on Circuits and Systems Ⅱ: Express Briefs, 2020, 67(11): 2345. DOI:10.1109/TCSⅡ.2020.2976983 |
| [11] |
BUHR S, HOYER M, KREIBIG M, et al. A 10 bit phase-interpolator-based digital-to-phase converter for accurate time synchronization in ethernet applications[C]//2020 27th IEEE International Conference on Electronics, Circuits and Systems (ICECS). Glasgow: IEEE, 2020: 3. DOI: 10.1109/ICECS49266.2020.9294824
|
| [12] |
LI Tong, XIONG Liang, YIN Yun, et al. A wideband digital polar transmitter with integrated capacitor-DAC-based constant-envelope digital-to-phase converter[C]//2019 IEEE Radio Frequency Integrated Circuits Symposium (RFIC). Boston: IEEE, 2019: 84. DOI: 10.1109/RFIC.2019.8701803
|
| [13] |
WU Guoying, HUANG Deping, LI Jingxiao, et al. A 1- 16 Gb/s all-digital clock and data recovery with a wideband high-linearity phase interpolator[J]. IEEE Transactions on Very Large Scale Integration Systems, 2016, 24(7): 2514. DOI:10.1109/TVLSI.2015.2418277 |
| [14] |
LIU Wenwen, LIN Min, SHI Jingwei, et al. High throughput low complexity and low power ePiBM RS decoder using fractional folding[J]. IEEE Transactions on Circuits and Systems Ⅱ: Express Briefs, 2021, 68(8): 2832. DOI:10.1109/TCSⅡ.2021.3070359 |
| [15] |
LO Y L, CHOU P Y, CHENG H H, et al. An all-digital DLL with dual-loop control for multiphase clock generator[C]//2011 13th International Symposium on Integrated Circuits (ISIC). Singapore: IEEE, 2011: 389. DOI: 10.1109/ISICir.2011.6131978
|
| [16] |
DEHNG G K, HSU J M. Clock-deskew buffer using a SAR-controlled delay-locked loop[J]. IEEE Journal of Solid-State Circuits, 2000, 35(8): 1131. DOI:10.1109/4.859501 |
 2024, Vol. 56
2024, Vol. 56


