2. 西安市智慧高速公路信息融合与控制重点实验室(长安大学),西安 710064;
3. 长安大学 信息工程学院,西安 710064
2. Xi'an Key Laboratory of Intelligent Expressway Information Fusion and Control (Chang'an University), Xi'an 710064, China;
3. School of Information Engineering, Chang'an University, Xi'an 710064, China
随着计算机技术的发展,涌现大量的目标跟踪算法,根据观测模型的策略差异,分为生成式模型及判别式模型。相关滤波器作为判别式模型的经典技术,在2010年首次被应用在目标跟踪领域中,提出了MOSSE(minimum output sum of squared error)算法[1],通过单通道的灰度特征训练分类器,并利用当前帧的区域与滤波器的响应峰值计算目标的最优位置。2012年, 文献[2]提出了核循环结构跟踪(circulant structure of tracking-by-detection with kernels,CSK)算法,在MOSSE基础上通过循环矩阵生成大量的样本,弥补了样本冗余的缺陷,并利用核函数加快了模型的计算速度。文献[3]又在CSK基础上引入了多通道方向梯度直方图(histogram of oriented gradient,HOG)特征,提出了一种核相关滤波器(kernelized correlation filters,KCF)算法,在改善跟踪精度的同时,利用傅里叶对角化加快了跟踪速度。文献[4]提出了一种特征融合尺度自适应核相关滤波器(scale adaptive with multiple features tracker,SAMF),利用尺度池的方法有效解决了目标跟踪中的尺度变化问题,并将HOG特征、灰度特征和CN特征三者融合提高跟踪的精度。文献[5]提出了判别尺度空间跟踪(discriminative scale space tracking,DSST)算法,包含的2个滤波器分别解决尺度与定位的问题,共有33个尺度变化,滤波器独立运作的模式使得算法便于移植,但额外提升了工作量,还存在边界效应等问题。文献[6]提出了空间正则化判别式相关滤波器(spatially regularized discriminative correlation filters,SRDCF),引入空间正则化,加入惩罚机制消除离响应中心过远的信号,但破坏了模型的封闭解,迭代方式也导致算法实时性差。
近些年来,学术界对群智能算法[7-11]的研究呈现指数趋势增长,提出了一批新的算法。文献[12]提出了基于改进细菌觅食算法的目标跟踪器,文献[13]提出了基于萤火虫算法(firefly algorithm, FA)的跟踪器,采用空间颜色直方图及Bhattacharyya系数,表现出较好的鲁棒性。随后文献[14]又提出了基于核空间颜色直方图特征的花授粉算法(flower pollination algorithm,FPA)的跟踪器。文献[15]提出了一种基于教学优化与正余弦优化混合的跟踪算法,表现出很强的竞争力。文献[16]受飞蛾趋光性启发,提出了飞蛾扑火优化(moth-flame optimization,MFO)算法,为优化领域提供了一种新的螺旋搜索范式,其收敛速度快的特点为代替传统的基于滤波的跟踪方法提供了一种可能,通过对目标多特征点的全局搜索可以完成高精度的目标跟踪。据此,本文提出了一种飞蛾扑火优化的尺度比例感知空间跟踪器,通过置信度将MFO跟踪框架与尺度比例感知空间跟踪器相结合,解决了尺度变化与长期跟踪目标丢失的问题,同时在无人机长期跟踪数据集上验证了性能。
1 飞蛾扑火算法跟踪器框架的设计基于约束优化的匹配跟踪问题通常由初始化、特征提取、目标匹配3个关键部分组成。本文采用MFO作为目标匹配搜索方法,设计了跟踪器框架。
1.1 跟踪器框架初始化方法设计传统MFO算法中,种群初始化通常为随机分布,表达式如下:
| $ \boldsymbol{M}_i^t=\left[m_{i, 1}^t, m_{i, 2}^t, \cdots, m_{i, d}^t\right] \quad i=1, 2, \cdots, n $ | (1) |
式中飞蛾Mit为第t时刻种群第i只飞蛾的初始位置,首次迭代时根据各维度的上下界随机均匀分布,上下界l及u由式(2)~(3)给出:
| $ \boldsymbol{l}=\left[x_{\min , 1}, x_{\min , 2}, \cdots, x_{\min , d}\right] $ | (2) |
| $ \boldsymbol{u}=\left[x_{\max , 1}, x_{\max , 2}, \cdots, x_{\max , d}\right] $ | (3) |
式中xmax, d和xmin, d为飞蛾第d维度的上限和下限。
群体智能需要维护一组解,并利用启发式规则搜索最优解。初始种群为后续演化过程提供一组初始猜想,决定了寻找全局起点,影响种群收敛速度和最终解精度。本文用高斯分布初始化取代MFO的随机初始化,通过2帧中目标位置预测运动轨迹,让种群初始化尽可能靠近预测目标区域,充分利用飞蛾个体的搜寻能力,缩短全局寻优时间,更快定位到局部目标。飞蛾Mit满足多维高斯分布,表达式如下:
| $ \begin{aligned} p\left(\boldsymbol{M}_i^{\boldsymbol{t}}\right)= & \frac{1}{(2 \pi)^{d / 2}\left|\sum^t\right|^{1 / 2}} \times \\ & \exp \left\{-\frac{1}{2}\left(\boldsymbol{M}_i^t-\boldsymbol{\mu}^t\right)^{\mathrm{T}} \sum^{-1}\left(\boldsymbol{M}_i^t-\boldsymbol{\mu}^t\right)\right\} \end{aligned} $ | (4) |
式中∑t和μt分别为t时刻的初始化种群的协方差矩阵及均值,均值与预测得出的目标位置有关,计算式见式(5)~(6):
| $ \boldsymbol{v}^t=\boldsymbol{M}_{\text {best }}^{t-1}-\boldsymbol{M}_{\text {best }}^{t-2} $ | (5) |
| $ \boldsymbol{\mu}^t=\boldsymbol{M}_{\text {best }}^{t-1}+\boldsymbol{v}^t $ | (6) |
式中Mbestt为t时刻由MFO算法求得的最优解。
在高斯初始化模型中,由前2帧得到目标位置的运动距离确定当前帧模型的速度,作为高斯模型的均值,计算当前帧飞蛾种群的初始位置。该模型能将飞蛾尽可能聚集到将要定位的目标位置,减少飞蛾种群的算力消耗,使算法从全局寻优快速地过渡到局部寻优。此外,当目标发生突变时,也可以由少量分布在目标疑似区周围的飞蛾引领种群定位目标。
1.2 特征提取目标跟踪过程中,特征提取将目标信息转化为数字信息,利用矩阵或者向量完成空间映射。FHOG(fast histogram of oriented gradients)[17]通过结合局部区域的无、有符号方向梯度直方图来表述特征,拥有对跟踪目标光照和目标形状变化不敏感的优势,在无人机场景下表述行人、车辆等物体特征具有较好的鲁棒性。因此,选用FHOG特征对跟踪目标的特征进行提取,具体步骤如下:
1) 建立像素级特征映射。计算每个像素(x, y) 的梯度大小和方向,幅值G(x, y)和梯度方向θ(x, y) 见式(7)~(8):
| $ G_x(x, y)=I(x+1, y)-I(x-1, y) $ | (7) |
| $ G_y(x, y)=I(x, y+1)-I(x, y-1) $ | (8) |
式中: Gx(x, y)和Gy(x, y)为(x, y)处x轴和y轴方向梯度。幅值G(x, y)和梯度方向α(x, y)见式(9)~(10):
| $ G(x, y)=\sqrt{G_x(x, y)^2+G_y(x, y)^2} $ | (9) |
| $ \alpha(x, y)=\tan ^{-1}\left[\frac{G_y(x, y)}{G_x(x, y)}\right] $ | (10) |
2) 空间聚合。通过像素级特征映射的空间聚合来得到基于cell的特征映射,也就是每一个cell一个特征,将图像分割为4×4的cell,将cell内的梯度幅值加权并投影到9个通道。提取过程见图 1。

|
图 1 提取cell的梯度直方图 Fig. 1 Extracting the gradient histogram of the cell |
3) 归一化和截断。梯度对偏置改变具有不变性,通过归一化获得。此处定义了4种不同的归一化因子,每个因子都包含4个cell的能量,归一化因子定义见式(11):
| $ \begin{aligned} N_{\delta \gamma}(i, j)= & \|\boldsymbol{C}(i, j)\|^2+\|i+\delta, j\|^2+ \\ & \|\boldsymbol{C}(i, j+\gamma)\|^2+\|\boldsymbol{C}(i+\delta, j+\gamma)\|^2 \end{aligned} $ | (11) |
式中: δ、γ取值范围为{-1,1},C(i, j)为基于cell特征特征映射的向量表示,对cell级特征进行归一化并截断,将得到的特征串联起来就得到了FHOG特征,FHOG特征目标候选区域的方向敏感和不敏感区域进行映射并对其进行归一化及截断处理。统计得到的对方向敏感的特征有18维,对方向不敏感的特征有9维,此外还包括4维的累加特征,共获取了18+9+4=31维的特征。FHOG特征详细描述了跟踪目标的边缘信息,通过局部形状特征化在描述信息上有良好的表现,并对光照强度的变化有适应性。FHOG特征可视化见图 2。

|
图 2 FHOG特征可视化 Fig. 2 FHOG feature visualization |
基于MFO的跟踪框架主要通过飞蛾围绕火焰做螺旋曲线运动更新飞蛾个体的位置,并在迭代完成后选取最优火焰作为目标的最佳匹配对象。这种更新模式虽然保证了飞蛾前期的全局寻优以及后期的局部寻优性能。但在此过程中,飞蛾种群在迭代初期围绕局部火焰更新需要多次迭代才能靠近最优火焰,同时,适应度低的飞蛾不能较快的达到最优火焰周围的局部区域,致使算法寻优效率过慢,在精度要求越高的场合,算法运算效率越低。图 3为MFO在优化过程中出现的2种局限性。

|
图 3 飞蛾扑火算法局限性 Fig. 3 Limitations of moth-flame algorithm |
图 3(a)为个体脱离最优群体的情况,距离火焰较近的飞蛾需要以较小的步长围绕火焰进行局部寻优,而脱离最优种群的飞蛾与群体之间距离较远,需要给定较长的移动距离进行调节,从而快速追上群体。因此,飞蛾个体需要通过调节个体与火焰距离的大小进行更新。图 3(b)为种群脱离最优解的情况,飞蛾在次优火焰周围运动,并会围绕自身对应的次优火焰更新,在这种情况下,次优火焰距离最优解较远,飞蛾种群需要多次迭代才能靠近最优解。因此,飞蛾种群需要给定一个向最优解的牵引,使得飞蛾种群脱离局部最优解从而靠近最优目标。
因此,根据迭代次数决定飞蛾的更新幅值的策略具有较大的局限性,且2种情况在更新中会交替发生,若依靠传统的非线性递减的参数模式会大幅降低算法的寻优效率,因此,设计了飞蛾的趋光性及聚集性来解决MFO的局限性。
1.3.2 改进的飞蛾扑火优化算法φi(k)为个体飞蛾趋光速率,其值越大表示个体飞蛾向最优火焰的飞行速率越快,表达式如下:
| $ \boldsymbol{\varphi}_i(k)=\frac{\boldsymbol{O}_M^{\text {best }}(k)-\boldsymbol{O}_{M, i}(k)}{\boldsymbol{O}_M^{\text {best }}(k)-\boldsymbol{O}_{M, i}(k-1)+\boldsymbol{\tau}} $ | (12) |
式中:OM, i(k)为第i只飞蛾在第k次迭代的适应度,OMbest(k)为第k次迭代时种群的最优适应度值,τ为正则项,防止分母为零。由个体的趋光速率提出了飞蛾个体趋光度的概念,如下所示:
| $ \boldsymbol{\rho}_i(k)=\frac{\boldsymbol{O}_M^{\text {best }}(k)-\boldsymbol{O}_{M, i}(k)}{\boldsymbol{\varphi}^{\text {best }}(k) \boldsymbol{O}_M^{\text {best }}(k)-\boldsymbol{\varphi}_i(k) \boldsymbol{O}_{M, i}(k-1)+\boldsymbol{\tau}} $ | (13) |
式中:ρi(k) 为第i只飞蛾趋光度,φbest(k) 为第k次迭代时飞蛾种群的最大趋光速率,则种群趋光度如下:
| $ \boldsymbol{\rho}_M(k)=\frac{1}{N} \sum\limits_{i=1}^N \boldsymbol{\rho}_i(k) $ | (14) |
式中ρM(k) 为整个种群的趋光度,当种群的趋光度高时,表示种群以一个较小的运动趋势向理想火焰目标缓慢靠近,当种群的趋光度低时,则代表种群大部分个体在最优火焰周围震荡。因此,需要通过种群的趋光度调整参数r(k) 从而改变种群的运动状态,参数r(k) 调整见式(15):
| $ \boldsymbol{r}(k)=\boldsymbol{r}_{\text {min }}+\boldsymbol{\rho}_M(k)\left(\boldsymbol{r}_{\text {max }}-\boldsymbol{r}_{\min }\right) $ | (15) |
式中rmin及rmax分别为参数r(k) 的下界及上界。
此外,飞蛾个体当距离火焰过远时,较大的步长通常会导致飞蛾以较大惯性越过火焰,导致收敛发散,而以较小步长则会导致收敛过慢,当飞蛾距离火焰较近时反之。因此,需要给飞蛾个体一个惩罚项,定义为飞蛾的聚集度 βi,见式(16):
| $ \boldsymbol{\beta}_i=\frac{1-\boldsymbol{O}_{M, i}}{1-\frac{1}{N} \sum\limits_{i=1}^N \boldsymbol{O}_{M, i}} $ | (16) |
通过式(16)调整飞蛾的更新距离,使得MFO快速收敛。则飞蛾更新轨迹改进为
| $ \boldsymbol{M}_i=\boldsymbol{\beta}_i \boldsymbol{D}_i^{k-1} \boldsymbol{e}^{b t} \cos (2 \pi t)+\boldsymbol{F}_j^{k-1} $ | (17) |
改进MFO的流程见图 4。

|
图 4 改进飞蛾扑火算法流程 Fig. 4 Flow chart of improved moth-flame algorithm |
基于优化算法的跟踪策略是利用目标模板与当前帧的图像进行匹配。跟踪过程中,跟踪目标时刻发生着角度、光照、尺度等的变化,若采用首帧模板持续作为后续视频序列的跟踪目标模板,目标形变时会导致跟踪丢失。因此,需要在跟踪框架中加入一个模板学习机制,保证时刻学习最新的目标特征更新目标模板。更新会在新一帧引入背景干扰因素,需以较低学习率引入新的特征进行学习,保证干扰因素造成的误差在可接受的范围内。因此,采用模板更新机制对目标模板进行补偿,见式(18):
| $ \gamma(t)=(1-\phi) \gamma(t-1)+\phi \gamma_{\text {best }}(t-1) $ | (18) |
式中:γ(t)为t时刻的目标模板特征,参数ϕ为模板特征的学习率。
1.5 飞蛾扑火优化跟踪器跟踪目标由跟踪视频序列图像中的像素坐标位置及目标的尺度构成,因此,设飞蛾变量Mi=[mxi, myi, s],其中mx1、myi为飞蛾变量Mi在图像中的像素坐标位置,s为跟踪目标的尺度因子,假设目标尺度不变,飞蛾即代表了搜寻的模板,并通过围绕最优火焰螺旋更新引领飞蛾个体定位到最终目标,这种交互机制使得火焰及飞蛾种群向理想目标运动的同时,飞蛾个体在火焰的周围探索避免陷入局部最优。
因此,在MFO更新机制的基础上,提出了一种基于改进的新型跟踪框架,流程见图 5,跟踪目标由初始帧标定给出初始目标的坐标及尺度。同时,高斯初始化飞蛾种群的分布,利用FHOG特征提取飞蛾种群中每个个体的特征,再通过余弦相似度指标匹配特征模板与个体飞蛾之间的相似度。通过排序得出火焰后,利用改进后的MFO更新飞蛾位置,在迭代完成时输出跟踪结果,若非最后一帧,则更新匹配模板后进入下一帧跟踪。

|
图 5 基于改进飞蛾扑火算法的跟踪框架 Fig. 5 Tracking framework based on improved moth-flame algorithm |
针对MFO跟踪器无尺度变化、跟踪效率低的问题,本文在尺度滤波器的基础上加入比例感知滤波器,提出了一种尺度比例感知空间跟踪器(scale ratio aware space tracker,SRAST)调节长宽比变化。由于SRAST存在单FHOG特征不能应对多种复杂情况和长期跟踪下目标丢失的问题,将SRAST的思想融入动态多特征飞蛾扑火跟踪器,提出了一种新的无人机长期跟踪的算法MFO-SRAST。
2.1 SRAST的设计在DSST算法中,首先标定出涵盖图像的目标块(patch),从该图像块中计算获得d维的FHOG特征,其中第l维度的特征向量用 fl表示,l∈{1, …, d}。fl训练得到的滤波器用hl表示,最优滤波器h通过构建最小化代价函数得到,见式(19):
| $ \varepsilon=\left\|\sum\limits_{l=1}^d h^l * \boldsymbol{f}^l-g\right\|^2+\lambda \sum\limits_{l=1}^d\left\|h^l\right\|^2 $ | (19) |
式中:λ为正则化系数;*为循环相关,其目的是为了消除输入内的零频谱分量的影响;g为二维高斯标签,g的峰值为输入图像块的中心。为了避免式(19)的解为0,根据帕塞瓦尔定理,可以在频域求解:
| $ H^l=\frac{\bar{G} F^l}{\sum_{k=1}^d \bar{F}^k F^k+\lambda}=\frac{A_t^l}{B_l} \quad l=1, \cdots, d $ | (20) |
式中大写字母对应小写字母响应量的DFT变换,G为G的复共轭。实际应用中,最佳滤波器是通过最小化所有训练样本的输出误差得到,因此在各样本中的每一像素都要通过d×d维的求解,导致计算量过大。为了得到鲁棒相似的结果,定义Atl及Bl分别为第t-1帧滤波器的分子及分母。在第t帧中,分子和分母分别更新,见式(21)~(22):
| $ A_t^l=(1-\eta) A_{t-1}^l+\eta \bar{G}_t F_t^l $ | (21) |
| $ B_t^l=(1-\eta) B_{t-1}+\eta \sum\limits_{k=1}^d \bar{F}_t^k F_t^k $ | (22) |
式中学习率η决定了滤波器的学习速度。当前时刻目标坐标利用计算最大响应值得到,见式(23):
| $ y = {F^{ - 1}}\left\{ {\frac{{\sum_{l = 1}^d {\overline {{A^l}} } {Z^l}}}{{B + \lambda }}} \right\} $ | (23) |
式中: F-1为傅里叶反变换,Zl为zl的傅里叶变换,y取最大值时z对应位置即为最终确定新目标位置。
当目标与无人机摄像头距离变化时,目标大小发生改变,因此,需要算法对尺度做出自适应设计,否则可能导致跟踪漂移或失败。DSST中一维独立的相关滤波器能适应目标的尺度变换。具体过程为:
1) 在新的一帧中,由上一帧得到的尺度大小与二维位置相关滤波器获得目标的新坐标。假设目标的尺寸大小为M1×N1,以目标图像的中央作为正中心,利用预设的S1个不同尺度因子估计其尺度变化,获得S1种不同尺寸的样本,其候选大小的依据如下:
| $ a^{n_s} M_1 \times a^{n_s} N_1 n_{\mathrm{s}} \in\left\{\left[-\frac{S_1-1}{2}, \cdots, \frac{S_1-1}{2}\right]\right\} $ | (24) |
式中:S1为尺度个数,a为尺度因子。
2) 计算各待测样本的特征,获得d维特征串联成一个特征向量,最终得到S1层尺度的滤波器。尺度滤波器获取特征与位置相关滤波器不同,位置滤波器以cell尺寸1×1获得FHOG特征,尺度相关滤波器以4×4的cell获得FHOG特征,并最后乘以汉明窗保证滤波的稳定性。
尺度滤波器中,通过给定S1种不同的尺度因子生成等长宽比的S1个样本,可以在视角远近变化时适应目标大小的变化。但目标角度发生改变时,固定的长宽比会导致跟踪定位到局部特征,并随着误差累积逐渐丢失目标。见图 6。

|
图 6 固定长宽比下的尺度变化效果 Fig. 6 Scale change effect under fixed aspect ratio |
假设尺度滤波器的尺度个数S1为33,若分别采用长尺度因子与宽尺度因子达到适应长宽比的目的,则尺度滤波器所需样本为1 089个,计算量随尺度个数增加呈指数增长,将会产生过多的无效样本导致滤波器丧失鲁棒性。因此,为了减小计算量,提升计算效率,在尺度滤波器的基础上加入比例感知滤波器,提出了SRAST调节长宽比变化。
类似于尺度滤波器的求解,比例感知滤波器在首帧初始化比例变化值n,见式(25):
| $ n_{\mathrm{r}} \in\left\{\left[-\frac{S_2-1}{2}, \cdots, \frac{S_2-1}{2}\right]\right\} $ | (25) |
比例因子c=(c1, c2)由nr排列组合而成,c1及c2分别为长与宽的比例,共生成S2(S2-1)+1种因子,在求解出的尺度因子基础上加入比例因子,则比例感知滤波器样本提取大小为c1nransM1×c2nransN1。通过计算样本的FHOG特征得到S2(S2-1)+1层不同比例的滤波器,在傅里叶域计算响应,所对应的最大值即为最终确定的比例因子。
2.2 MFO-SRAST的设计将SRAST得到的比例因子作为MFO尺度变化的依据,得到MFO-SRAST算法,MFO-SRAST的跟踪流程见图 7。

|
图 7 第t帧MFO-SRAST的跟踪器流程 Fig. 7 Tracking process of MFO-SRAST for t-th frame |
MFO-SRAST具体步骤为:
1) 初始化。MFO-SRAST模型首先提取第1帧样本的特征,训练得到初始模型并保存。
2) 位置滤波器定位。从第t(t>1)帧开始,根据第t-1帧目标位置获取目标周围的一片区域,计算该区域的FHOG特征,利用前一帧训练好的滤波器模型确定位置滤波器响应值。
3) 置信度判断。根据位置滤波器的响应峰值判断目标是否为丢失或被遮挡状态,若目标丢失则扩大检测区域,随机初始化后进入飞蛾扑火优化跟踪阶段。反之则继续判断目标是否产生形变等轻微干扰,若产生轻微干扰则采用高斯初始化初始种群。
4) MFO跟踪。利用自适应融合特征的飞蛾扑火优化跟踪检测目标位置信息。
5) 尺度更新。确定目标位置后,建立尺度金字塔提取尺度样本,通过尺度滤波器响应判断目标的最优尺度。
6) 比例更新。由确定的尺度因子与比例因子相乘,建立比例金字塔提取比例样本,计算比例感知滤波器的最大响应,确定目标的尺度变化,输出目标尺寸。
7) 输出第t帧目标跟踪结果。结合改进后的MFO输出跟踪目标位置信息和SRAST输出的目标尺寸信息,输出第t帧目标跟踪结果。
8) 更新目标模板。融合跟踪算法采用双模板更新策略。在判断目标不可信时,停止更新滤波器模板,并单独进行MFO跟踪器的动态模板更新;判断目标可信时,恢复滤波器模板更新,完成对下一帧目标的跟踪。
3 基于置信度的重检测指标SRAST算法在面临遮挡、运动突变等复杂情况时,模型长时间学习到遮挡物信息使得跟踪器难以识别跟踪目标导致目标丢失,不适宜作为长期跟踪算法。因此本文设计了一种重检测指标反映跟踪的置信度,通过置信度判断跟踪状态,并在跟踪不可靠时引入MFO跟踪框架重新找回跟踪目标。在目标跟踪领域中目前常见的指标有两种:
1) 第一种为最大响应分数Fmax, 其表达见式(28):
| $ F_{\text {max }}=\max F(\Delta x, \Delta y) $ | (28) |
其中F(Δx, Δy)为目标检测范围水平方向位移Δx及垂直方向位移Δy后的响应。
2) 第二种为平均峰值相关能量A(average peak correlation energy,APCE),见式(29):
| $ A=\frac{\left|F_{\max }-F_{\min }\right|^2}{\operatorname{mean}\left(\sum\limits_{x, y}\left(F\left(x^{\prime}, y^{\prime}\right)-F_{\text {min }}\right)^2\right)} $ | (29) |
式中:mean为取平均值,Fmin为目标检测范围内的最小响应值。跟踪目标响应图的震荡程度及峰值能反映目标的置信水平。对于较轻微的形变和噪声,响应图反映为一个平滑上升尖锐的区域。当目标遭遇遮挡等复杂情况时,峰值及APCE会剧烈下降。
如图 8所示,当目标没有任何形变和遮挡等复杂情况时,响应为中心平滑上升的单峰,APCE指标值较大。当目标被干扰时,滤波器响应的旁瓣上升,出现多个伪峰值,主峰值与旁瓣的峰值对比度降低,APCE指标大幅度下降。因此,本文采用最大响应峰值与APCE综合判别跟踪的置信度。具体判别方法为:当Fmax<ρstop且A<ζstop时,目标被判断为丢失或被遮挡状态;当ρstop<Fmax<ρint且ζstop<A<ζint时,跟踪目标被判定为形变等干扰。其中,ρstop及ζstop为目标丢失阈值,ρint及ζint为干扰阈值。

|
图 8 APCE指标随环境变化示意 Fig. 8 Schematic of APCE index changing with environment |
本实验硬件平台为Intel(R) Core(TM) i7-9750H CPU @2.60 GHz,内存RAM 16.0 GB的计算机,软件平台为MATLAB 2020a。长期跟踪实验数据集采用UAV20L中的car1、car9、person2、group1视频序列,以及UAV123中尺度变化明显的boat4视频序列。本文算法用MFO_SRAST表示,实验对比算法为CN、CSK、KCF、fDSST、SAMF[4]、DSST[5]、ECO_HC[18]、AutoTrack[19]、Staple_CA[20]、Staple[21]、BACF[22]及lct[23]。实验中,设种群数目n=15,最大迭代次数k=30,调节参数δ=10,ξ=5,最大模板学习率ϕmax=0.04。SRAST参数设置为:S1=33,S2=5,ρstop=0.5×Fmax,ζstop=0.6×A,ρstop=0.3×Fmax,ζstop=0.35×A,其中,Fmax和A为到当前帧数前所有视频序列最大响应峰值与APCE指标的平均值,尺度因子a=0.02,比例因子c1=c2=0.02。
4.2 定性分析实验包含尺度变换、部分遮挡、相似目标、完全遮挡、离开视野、形变、阴影等多种场景。
由图 9可以看出,在序列133帧之前,各跟踪算法均保持稳定跟踪。在序列500帧时,目标车辆尺度发生变化,多数对比跟踪算法无法更新尺度大小,MFO_SRAST依旧稳定。在1022帧时,目标发生部分遮挡及形变,此时由于目标尺度变化且伴随着旋转、部分对比算法已经发生轻微漂移。在1537帧左右车辆目标被完全遮挡。由1685帧可以看出,此时只有MFO_SRAST在遮挡结束后重新跟踪上目标,其他对比算法由于对遮挡物的无效特征学习累积,导致完全丢失目标。1941帧左右目标靠近图像边缘,几乎移除视野,此时MFO_SRAST保持跟踪不丢失,但由于误差的累积,跟踪发生偏移。对比实验可知,MFO_SRAST算法在目标发生部分遮挡、完全遮挡、尺度变化等复杂环境具有更好的适应性。

|
图 9 car1视频序列定性分析 Fig. 9 Qualitative analysis of video sequences car1 |
由图 10可知,person2视频序列中目标主要存在形变、摄影角度变化、尺度变化等复杂情况。在前434帧时,各算法均能稳定跟踪。在675帧时,CN随着误差的累积逐渐产生漂移,在846帧BACF跟踪尺度发生不规则变化。从1375帧到1760帧时,Staple_CA、Staple算法尺度跟踪失败,并在2462帧丢失目标。其余算法在此数据集上表现较好。实验可以看出,MFO_SRAST在摄影角度变化、形变等环境下能稳定跟踪目标。

|
图 10 person2视频序列定性分析 Fig. 10 Qualitative analysis of video sequences person2 |
如图 11所示,boat4视频序列中的目标主要存在尺度变化、视角变化、遮挡等复杂情况。在191帧时目标发生尺度及视角变化,多数跟踪算法定位到目标局部特征,MFO_SRAST则能及时适应目标长宽比变化。在300帧时,目标发生光照变化,各算法可以保持稳定跟踪目标。在553帧时,BACF产生跟踪漂移,ECO_HC跟踪精度较高,但无法适应长宽比变化,而MFO_SRAST跟踪效果较好,能完全标定出目标轮廓,在目标长宽比及尺度变换下具有较好的跟踪性能。

|
图 11 boat4视频序列定性分析 Fig. 11 Qualitative analysis of video sequences boat4 |
如图 12所示,car9视频序列包含尺度变换、遮挡、相似目标、角度变化等复杂情况。在350帧时,目标尺度大幅度变化,KCF、CSK、lct尺度不变,lct出现目标跟踪丢失,其余各算法均能跟踪目标。在第800帧时出现严重遮挡,由888帧可以看出遮挡后只有BACF及MFO_SRAST能稳定跟踪目标,lct定位到相似车辆导致跟踪失败。在1300帧时STAPLE-CA同样定位到相似目标车辆。1879结束帧时无人机摄像角度发生改变,MFO_SRAST相比BACF能更准确跟踪目标,跟踪窗更贴合目标轮廓。

|
图 12 car9视频序列定性分析 Fig. 12 Qualitative analysis of video sequences car9 |
图 13所示的group1视频序列中的目标存在严重遮挡、角度变化、光照变化及相似目标等复杂情况。在97帧时,BACF算法受相似目标干扰丢失目标。在575帧时目标遭遇阴影及角度变化,CN算法由于对光照变化较为敏感从而产生漂移。1314帧KCF,Staple_CA和CSK算法被干扰定位到相似目标。在2764帧时产生严重遮挡,对比算法大都跟踪失败。在3326帧时AutoTrack及DSST产生不同程度的漂移,而MFO_SRAST跟踪依旧稳定。在4572帧视频序列结束时,只有MFO_SRAST与ECO_HC依旧稳定跟踪目标,且MFO_SRAST跟踪较为精确。从实验可以看出,MFO_SRAST在相似目标、视角变化、遮挡等复杂情况下具有较好的跟踪性能。

|
图 13 group1视频序列定性分析 Fig. 13 Qualitative analysis of video sequences group1 |

|
图 14 13种算法在car1视频序列上的实验效果 Fig. 14 Experimental results of 13 algorithms on video sequences car1 |

|
图 15 13种算法在person2视频序列上的实验效果 Fig. 15 Experimental results of 13 algorithms on video sequences person2 |
|
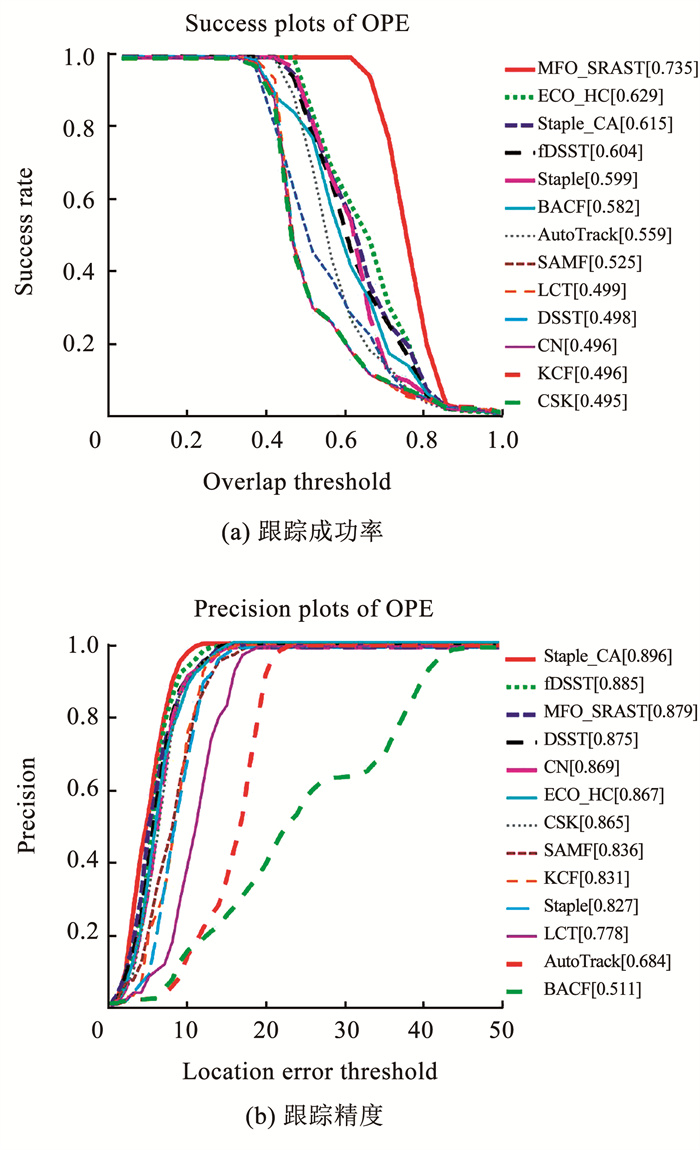
图 16 13种算法在boat4视频序列上的实验效果 Fig. 16 Experimental results of 13 algorithms on video sequences boat4 |
|
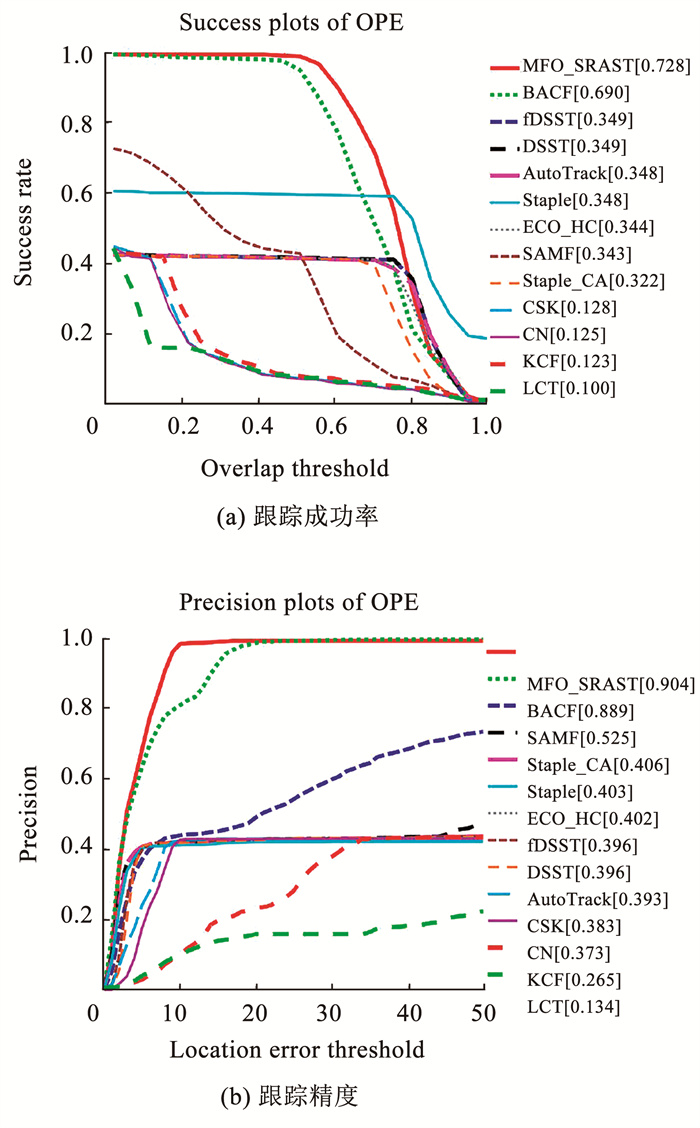
图 17 13种算法在car9视频序列上的实验效果 Fig. 17 Experimental results of 13 algorithms on video sequences car9 |

|
图 18 13种算法在group1视频序列上的实验效果 Fig. 18 Experimental results of 13 algorithms on video sequences group1 |
图 14为各算法在car1视频序列的跟踪成功率及精确度,MFO_SRAST的跟踪成功率及精确度分别为41.2%和70.7%,在所有对比算法中排名第一。与在此数据集表现较好的fDSST相比,跟踪成功率及精确度分别提升了3.6%和11.0%,与ECO-HC相比,跟踪成功率及精确度分别提升了2.6%和12.7%,对比其余算法均有大幅上升。
由图 15可知,在跟踪成功率上MFO_SRAST相比AutoTrack和ECO-HC分别高3.1%与6.4%,在跟踪精确度上相比ECO-HC提升了2.5%,比AutoTrack提升了4.0%。DSST在中心位置误差评价上表现较好,但比MFO_SRAST较低。除此之外,相对比其余算法均有稳定提升,综合来看,MFO_SRAST表现最好。
由图 16可知,boat4视频序列主要面临的复杂情况为尺度与光照变化,MFO_SRAST在重叠率上表现优异,远高于其余对比算法,比排名第二的ECO_HC高出了10.6%。在跟踪精度方面,MFO_SRAST、Staple_CA和Fdsst算法精度相差较小,对比其余算法MFO_SRAST均表现出明显优势。综合来看,引入比例变化的MFO_SRAST在跟踪重叠率上有较大的提升,跟踪精度与其他算法相比也有明显的优势。
由图 17可知,car9视频序列上,MFO_SRAST以成功率72.8%及跟踪精确度90.4%排名第一,相比BACF算法跟踪成功率及准确度分别提升了3.8%及1.5%;其余算法表现差异较大。其中fDSST与DSST算法跟踪成功率为34.9%,比MFO_SRAST算法低37.9%。在中心位置误差评价指标上MFO_SRAST算法相比排名第三的SAMF算法高37.9%。
由图 18可知,各跟踪算法在group1视频序列上性能差距明显,MFO_SRAST跟踪成功率与精度分别为61.9%与82.6%,在跟踪成功率上与ECO_HC相比低0.8%,但在跟踪精度上比ECO_HC高0.9%,因此在本视频序列上2算法差异较小。与排名第三的SAMF相比,在跟踪成功率与精度上分别提升了4.0%和7.8%,对比其余算法,MFO_SRAST性能表现优异,综合来看,MFO_SRAST相比其他算法具有更好的跟踪性能。
综合定性分析与定量分析来看,MFO_SRAST能应对长宽比尺度变换的复杂情况,并在应对其他长期跟踪遭遇的复杂环境干扰时有较强的鲁棒性,跟踪精度也有明显的提升。因此,MFO_SRAST可较好提升无人机长期跟踪的稳定性并解决目标尺度变换的问题。
4.4 跟踪性能分析为了具体展现本算法的性能,对各实验视频序列的定量分析结果取均值,见表 1。MFO_SRAST在平均跟踪成功率和精度都优于其他算法。在平均跟踪速度方面,除去精度和成功率都较低的比较算法之外,在2个指标都略低于本文算法的SAMF、ECO_HC和AutoTrack跟踪算法中,也只有ECO_HC实时性稍高。但MFO_SRAST的平均跟踪速度可以达到27帧/s,完全满足了实时性的要求,综合来看,MFO_SRAST相比于其他比较算法性能最佳,应用价值明显。
| 表 1 不同算法实时性比较 Tab. 1 Real-time comparison of different algorithms |
提出了一种基于MFO优化的尺度比例感知空间跟踪器。首先,详细阐述了群体智能算法的寻优原理,以及其应用在跟踪算法的可行性。实现了原始的MFO的初始化策略的改进,并结合快速梯度直方图特征构造了改进的飞蛾扑火优化跟踪器。其次,提出了一种比例感知滤波器用以适应跟踪目标长宽比变化。最后,根据置信度指标将MFO优化器与SRAST跟踪算法相结合,弥补2种算法的优缺点,从而实现无人机航拍下长期的稳定跟踪。将提出的算法与同类文献在UAV123及长期跟踪数据集UAV20L上进行了对比。实验结果表明,MFO_SRAST算法在长期跟踪上具有稳定的性能,且有效地解决了尺度变换与跟踪遮挡等问题,满足实时性的要求, 具有明显的应用价值。飞蛾扑火优化算法的跟踪框架没有相关滤波中边界效应等限制,在应对目标突变等复杂情况时有较好的效果,但由于在搜索过程中目标与背景被赋予相同的特征权值,在搜索过程中容易造成目标与背景的冲突。因此,该问题需要在接下来的工作中进一步完善。
| [1] |
BOLME D S, ROSS BEVERIDGE J, DRAPER B A, et al. Visual object tracking using adaptive correlation filters[C]//IEEE Computer Society Conference on Computer Vision and Pattern Recognition. San Francisco: IEEE, 2010: 2544. DOI: 10.1109/CVPR.2010.5539960
|
| [2] |
HENRIQUES J F, CASEIRO R, MARTINS P, et al. Exploiting the circulant structure of tracking-by-detection with kernels[C]//European Conference on Computer Vision. Berlin: Springer, 2012: 702. DOI: 10.1007/978-3-642-33765-9_50
|
| [3] |
HENRIQUES J F, CASEIRO R, MARTINS P, et al. High-speed tracking with kernelized correlation filters[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2014, 37(3): 583. DOI:10.1109/TPAMI.2014.2345390 |
| [4] |
LI Yang, ZHU Jianke. A scale adaptive kernel correlation filter tracker with feature integration[C]//Proceedings of the European Conference on Computer Vision. Berlin: Springer, 2014: 254. DOI: 10.1007/978-3-319-16181-5_18
|
| [5] |
DANELLJAN M, HÄGER G, KHAN F S, et al. Accurate scale estimation for robust visual tracking[C]//British Machine Vision Conference. Nottingham: BMVA, 2014: 1 DOI: 10.5244/C.28.65
|
| [6] |
DANELLJAN M, HÄGER G, KHAN F S, et al. Learning spatially regularized correlation filters for visual tracking[C]//Proceedings of the IEEE International Conference on Computer Vision. Santiago: IEEE, 2015: 4310. DOI: 10.1109/ICCV.2015.490
|
| [7] |
黄鹤, 李文龙, 吴琨, 等. 基于ALCE-SSA优化的三维无人机低空突防[J]. 南京大学学报(自然科学), 2022, 58(3): 448. HUANG He, LI Wenlong, WU Kun, et al. 3D UAV low altitude penetration optimization based on ALCE-SSA[J]. Journal of Nanjing University(Natural Science), 2022, 58(3): 448. DOI:10.13232/j.cnki.jnju.2022.03.009 |
| [8] |
黄鹤, 李潇磊, 杨澜, 等. 引入改进蝠鲼觅食优化算法的水下无人航行器三维路径规划[J]. 西安交通大学学报, 2022, 56(7): 9. HUANG He, LI Xiaolei, YANG Lan, et al. Three dimensional path planning of unmanned underwater vehicle based on improved manta ray foraging optimization algorithm[J]. Journal of Xi'an Jiaotong University, 2022, 56(7): 9. DOI:10.7652/xjtuxb202207002 |
| [9] |
DHIMAN G, KUMAR V. Seagull optimization algorithm: theory and its applications for large-scale industrial engineering problems[J]. Knowledge-Based Systems, 2018, 165: 169. DOI:10.1016/j.knosys.2018.11.024 |
| [10] |
HASHIM F A, HUSSAIN K, HOUSSEIN E H, et al. Archimedes optimization algorithm: a new metaheuristic algorithm for solving optimization problems[J]. Applied Intelligence, 2020, 51: 1531. DOI:10.1007/s10489-020-01893-z |
| [11] |
ABUALIGAH L, YOUSRI D, ABD ELAZIZ M, et al. Aquila Optimizer: a novel meta-heuristic optimization algorithm[J]. Computers & Industrial Engineering, 2021. DOI:10.1016/j.cie.2021.107250 |
| [12] |
NGUYEN H T, BHANU B. Real-time pedestrian tracking with bacterial foraging optimization[C]//IEEE Ninth International Conference on Advanced Video and Signal-Based Surveillance. Beijing: IEEE, 2012: 37. DOI: 10.1109/AVSS.2012.60
|
| [13] |
GAO Mingliang, HE Xiaohai, LUO Daisheng, et al. Object tracking using firefly algorithm[J]. IET Computer Vision, 2013, 7(4): 227. DOI:10.1049/iet-cvi.2012.0207 |
| [14] |
GAO Mingliang, ZANG Yuanru, SHEN Jin, et al. Visual tracking based on flower pollination algorithm[C]//Proceedings of the 35th Chinese Control Conference. Chengdu: IEEE, 2016: 27. DOI: 10.1109/ChiCC.2016.7553956
|
| [15] |
FELZENSZWALB P F, GIRSHICK R B, MCALLESTER D, et al. Object detection with discriminatively trained part based models[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2010, 32(9): 1627. DOI:10.1109/TPAMI.2009.167 |
| [16] |
MIRJALILI S. Moth-flame optimization algorithm: a novel nature-inspired heuristic paradigm[J]. Knowledge-Based Systems, 2015(89): 228. DOI:10.1016/j.knosys.2015.07.006 |
| [17] |
黄鹤, 胡凯益, 宋京, 等. 雾霾线求解透射率的二次优化方法[J]. 西安交通大学学报, 2021, 55(8): 130. HUANG He, HU Kaiyi, SONG Jing, et al. A twice optimization method for solving transmittance with haze-lines[J]. Journal of Xi'an Jiaotong University, 2021, 55(8): 130. DOI:10.7652/xjtuxb202108016 |
| [18] |
DALAL N, TRIGGS B. Histograms of oriented gradients for human detection[C]//IEEE Computer Society Conference on Computer Vision and Pattern Recognition(CVPR'05). San Diego: IEEE, 2005: 886. DOI: 10.1109/CVPR.2005.177
|
| [19] |
DANELLJAN M, BHAT G, KHAN F S, et al. Eco: efficient convolution operators for tracking[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Honolulu: IEEE, 2017: 6638. DOI: 10.1109/CVPR.2017.733
|
| [20] |
LI Yiming, FU Changhong, DING Fangqiang, et al. Auto Track: towards high-performance visual tracking for UAV with automatic spatio-temporal regularization[C]//IEEE/CVF Conference on Computer Vision and Pattern Recognition(CVPR). Seattle: IEEE, 2020: 11920. DOI: 10.48550/arXiv.2003.12949
|
| [21] |
MUELLER M, SMITH N, GHANEM B. Context-aware correlation filter tracking[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Honolulu: IEEE, 2017: 1396. DOI: 10.1109/CVPR.2017.152
|
| [22] |
BERTINETTO L, VALMADRE J, GOLODETZ S, et al. Staple: complementary learners for real-time tracking[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas: IEEE, 2016: 1401, DOI: 10.1109/CVPR.2016.156
|
| [23] |
GALOOGAHI H K, FAGG A, LUCEY S. Learning background-aware correlation filters for visual tracking[C]//Proceedings of the IEEE International Conference on Computer Vision. Venice: IEEE, 2017: 1135. DOI: 10.1109/ICCV.2017.129
|
 2024, Vol. 56
2024, Vol. 56


