2. 亚热带建筑科学国家重点实验室(华南理工大学),广州 510640;
3. 广州珠江外资建筑设计院有限公司,广州 510060
2. State Key Laboratory of Subtropical Building Science(South China University of Technology), Guangzhou 510640, China;
3. Guangzhou Pearl River Foreign Investment Architectural Designing Institute Co., Ltd., Guangzhou 510060, China
弯矩作用下钢筋混凝土(RC)梁受拉区会产生裂缝,截面中性轴偏离形心轴并向受压区移动,导致RC梁形心轴产生轴向伸长[1]。现浇钢筋混凝土楼盖梁(以下称楼盖梁)的轴向伸长会受到竖向构件、楼板、相邻梁等构件的空间约束,从而产生轴向压力。已有试验表明,结构空间约束可提高楼盖梁受弯承载力[2-3]和受剪承载力[4],这是强震作用下框架结构“强柱弱梁”无法实现而发生整体倒塌的主要原因。
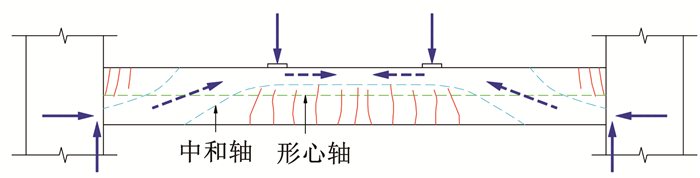
经典混凝土结构设计理论建立在静定的独立构件试验基础上,已被写入各国混凝土结构设计规范[5-6]并在工程中广泛应用。规范公式可较精确地计算简支梁受弯承载力[7],但不能反映结构空间约束的影响。如图 1所示,对楼盖梁进行两点加载,结构空间约束使其跨中纯弯段变成压弯受力状态,受弯承载力较简支梁发生显著变化,这是规范公式没有考虑的。
|
图 1 楼盖梁的两点加载受力 Fig. 1 Two-point loading of floor beam |
竖向荷载作用下约束轴力提高RC构件承载力的效应亦称为压拱效应。1955年,Ockleston通过对一栋3层建筑进行竖向加载时发现,压拱效应可使板的实际极限荷载达到塑性铰理论计算值的3~4倍[8-9];压拱效应在楼盖梁抗连续倒塌中具有重要作用[10-11],试验结果表明,压拱效应可使中柱失效的双跨楼盖梁承载力提高至塑性铰理论的2倍以上[12-13];RC梁承载力因压拱效应而提高的幅度与跨高比相关[14],而RC梁连续倒塌试验的试件为双跨梁,倒塌时跨高比是单跨梁的两倍,且目前单跨梁在轴向约束下受力的试验研究较少,有必要对单跨梁在被动轴压力下的受力性能展开试验研究。
考虑RC梁轴向约束的试验方法多为采用轴向约束装置对独立梁施加约束[15-17],并不能真实反映楼盖梁的实际边界条件。本文聚焦竖向荷载作用下楼盖梁跨中受弯性能,在框架结构中进行楼盖梁的构件试验,通过对比楼盖梁和简支梁的承载力、破坏形态及变形性能,研究结构空间约束改变楼盖梁跨中受弯性能的规律和机制。
1 试验设计 1.1 模型设计设计一栋2层3×3跨框架结构,一层为试验层,二层为反力层,如图 2所示。框架柱柱底平放于试验场地上,通过基础层梁相连。X向跨度为3 000 mm,Y向跨度为1 400 mm,各构件信息见表 1。试验层板厚hf为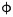
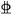


|
图 2 试验RC框架结构 Fig. 2 Test RC frame structure |
| 表 1 框架结构构件信息 Tab. 1 Information of components in the frame structure |
试验设计的楼盖梁变量包括空间位置(倒L形-边框边跨、倒L形-边框中跨、T形-中框边跨、T形-中框中跨)、底筋配筋率ρ(2.05%、1.62%、1.29%、0.86%),各楼盖梁的参数见图 2(c)及表 2。以KA-1.62为例,其配筋见图 3(a)。
| 表 2 楼盖梁试件信息 Tab. 2 Information of floor beam specimens |

|
图 3 试验梁配筋 Fig. 3 Reinforcement of beam specimen |
4条简支梁对比试件的几何、配筋参数见表 3。以R-2.05为例,其配筋见图 3(b)。
| 表 3 简支梁试件信息 Tab. 3 Information of simple supported beam specimen |
试验层采用C30混凝土,立方体抗压强度实测平均值fcu=36.7 MPa。板筋采用HPB300级钢筋,梁底纵筋及箍筋采用HRB400级钢筋,梁顶纵筋采用HPB300级钢筋,实测钢筋的力学性能见表 4。简支梁试件和结构试验层采用同一批次的混凝土和钢筋。
| 表 4 钢筋力学性能 Tab. 4 Mechanical properties of steel bars |
如图 4所示,采用100 t千斤顶通过分配梁进行两点加载,获得跨中800 mm长的纯弯段。同跨(中跨、边跨)不同榀的4根梁按挠度相同的原则同时加载,以消除平行相邻楼盖梁空间效应[18]所引起的荷载分担对楼盖梁承载力的贡献。在跨中底筋屈服前,楼盖梁的挠度较小,按荷载分级加载,纯弯段开裂前的每级增量为10 kN,开裂后的每级增量为20 kN。各楼盖梁屈服后,保持挠度相同,按位移控制分级加载,每级增量为2 mm。12根楼盖梁分3次进行试验,加载顺序为中跨(KB-2.05、KD-2.05、KD-0.86、KB-0.86)—西侧边跨—东侧边跨。边跨梁加载时,中跨梁已遭受一点的损伤,导致边跨梁所受的轴向约束刚度降低但影响程度较小。

|
图 4 试验加载装置 Fig. 4 Test setup |
简支梁采用两点对称加载,纯弯段长度与楼盖梁相同。跨中底筋屈服前按荷载控制分级加载,每级增量为10 kN,屈服后按位移控制分级加载,每级增量为2 mm。
1.4 测点布置测点包括:1)力传感器,测量施加的荷载;2)位移计,跨中位移计测量跨中挠度,梁端部水平位移计测量梁端轴向侧移;3)钢筋应变,包括梁纵筋和X向板筋的应变。在梁跨中纯弯段区域的所有纵筋上粘贴钢筋应变片,上部钢筋应变片相互错开一定距离(下部同),如图 3所示。在X向板筋的东西两侧与柱边重合的支座截面、X向跨中截面处粘贴钢筋应变片,以板B(西北部,与KA-1.62、KC-1.62相邻)为例,其X向板筋应变片布置见图 5。

|
图 5 板筋应变片布置(板B) Fig. 5 Layout of strain gauges on floor bars (slab B) |
楼盖梁和简支梁的典型裂缝分布如图 6所示(不是所有试件均出现图中标识的所有裂缝,具体见表 5)。楼盖梁加载初期,由于梁上部架立筋不伸入支座,两端梁柱交界处的上部出现垂直裂缝(⑤),且此裂缝的宽度在荷载P较小时就已达1.5 mm;加载至P=80~130 kN,跨中纯弯段下部受拉区出现裂缝(①),此后纯弯段裂缝数量逐渐增多并向上部延伸,弯剪区靠近加载点一侧出现由弯曲正裂缝发展而来的弯剪斜裂缝(②);加载至跨中挠度Δ=6.5~11 mm时,跨中受拉纵筋屈服,此后P-Δ曲线的上升速度明显降低,表现出塑性变形;随着挠度增加,两端弯剪区靠近柱边位置出现贯穿梁高的斜裂缝(③),而简支梁的弯剪区并未出现贯穿斜裂缝;P到达峰值荷载附近,纯弯段上部受压区混凝土出现保护层剥落现象(④),并逐渐压溃,导致试验梁最终破坏。

|
图 6 楼盖梁与简支梁试件裂缝分布 Fig. 6 Crack distribution of floor beam and simple supported beam |
| 表 5 各试验现象的发生时刻 Tab. 5 Occurrence time of each experimental phenomenon |
各梁试件的破坏形态符合适筋梁弯曲破坏的特征,梁试件因纵筋受拉屈服、跨中受压区混凝土压溃而破坏。与简支梁相比,楼盖梁的跨中受弯破坏形态并未因轴压力而发生显著改变,但因承载力显著提高,弯剪区承受的剪力也随之增加并达到受剪斜裂缝出现所需的剪力,甚至出现端部剪切破坏(KD-0.86)。部分试验梁的破坏形态如图 7所示,各现象点对应的荷载、挠度见表 5。

|
图 7 试验梁破坏形态 Fig. 7 Failure mode of beam specimens |
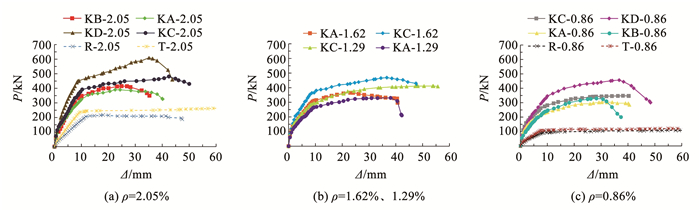
试验梁的荷载-跨中挠度(P-Δ)曲线如图 8所示。对于简支梁,开裂前Δ随P缓慢增加;开裂后,刚度有所下降,Δ随P近似线性增加;受拉纵筋屈服后,P-Δ曲线出现明显转折点,进入水平段直至跨中受压区混凝土压溃。对于楼盖梁,受拉纵筋屈服前,刚度不断下降,P-Δ曲线呈抛物线状上升;受拉纵筋屈服后,刚度明显下降,但P仍能随Δ增大而小幅度增大;P到达峰值后,混凝土压溃导致P下降。楼盖梁的自由伸长在加载过程中受到约束,从而产生随Δ增加的被动轴压力,这是楼盖梁的P-Δ曲线与简支梁不同的主要原因。
|
图 8 荷载-挠度曲线 Fig. 8 Load-deflection curve |
采用μ=Δy/Δu计算试验梁的延性系数[19],其中,Δy采用Park法[20]根据P-Δ曲线确定,Δu取P下降至90%峰值荷载对应的Δ(对于简支梁和部分楼盖梁,由于P-Δ曲线没有加载到荷载下降段的90%峰值荷载点,取试验结束时的Δ)。试验梁的延性系数如表 6所示,楼盖梁的μ平均值为4.38,分布范围为3.17~5.39,小于简支梁平均值7.19。由于楼板对混凝土受压区宽度b′f的贡献,T形简支梁的延性大于矩形简支梁。虽然楼盖梁跨中截面受弯时,楼板对楼盖梁b′f也有贡献从而提高延性,轴压力的存在却使得楼盖梁延性明显减小。
| 表 6 试验梁延性系数 Tab. 6 Ductility coefficient of beam specimens |
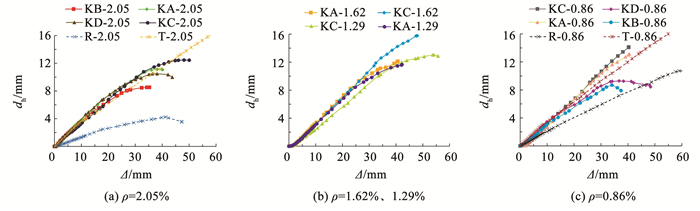
根据试验梁端部的水平位移计测量数据,计算试验梁两端支座距梁底150 mm(0.5倍梁高)位置的沿轴向水平侧移,两端支座相对侧移即为试验梁的轴向伸长dh。各试验梁的轴向伸长-挠度(dh-Δ)曲线如图 9所示。在加载前期,dh随Δ的增加而近似线性增大。在跨中受压区混凝土开始压溃后,dh增大速率明显变缓,甚至出现下降,这是因为跨中截面中性轴不再往上偏移,而是往形心轴方向反向移动,从而减小了形心轴的轴向伸长。
|
图 9 试验梁的dh-Δ曲线 Fig. 9 dh-Δ curve of beam specimens |
T形简支梁的dh明显大于矩形简支梁,这是由于T形简支梁b′f较大,受压区高度较小,中性轴偏移距离大,导致形心轴处的轴向伸长较大。在相同挠度下,楼盖梁的dh与T形简支梁相当。与简支梁相比,楼盖梁一方面受到约束轴力的作用,另一方面,除了跨中外,还在两端支座产生塑性区,而塑性区是产生轴向伸长的主要区域。
4根中跨位置楼盖梁的dh相近,8根边跨位置的楼盖梁亦如此。中跨楼盖梁的dh小于边跨楼盖梁,这也说明中跨楼盖梁所受到的轴向约束刚度较边跨楼盖梁大。达到承载力峰值时,中跨楼盖梁的dh最大值达到10 mm,边跨楼盖梁的dh最大值达到13 mm。楼盖梁周围的约束构件因楼盖梁的轴向伸长产生了变形,其中楼盖梁下方的基础层梁可观测到拉裂缝,意味着基础层梁亦产生了轴向伸长。在楼盖梁达到荷载峰值时,其轴向伸长会引起柱端产生不可忽视的侧移,应引起足够重视。
2.4 梁钢筋应变在试验梁纯弯段区域每一根纵筋上都粘贴有应变片,取架立筋或底筋应变的平均值,得到试验梁的架立筋应变εt和底筋应变εb,如图 10所示。

|
图 10 试验梁钢筋应变 Fig. 10 Bar strain of beam specimens |
加载开始后,εt减小(压应变增加),但其随后的变化趋势与纯弯段受压区高度c的大小有关。c较大时,εt继续减小;c较小时,εt发生转折开始增大,当c小于受压纵筋中心距梁上表面的距离a′s时,εt大于0(转为受拉)。由图 10可知,在加载前期,中框楼盖梁的εt较边框大,这是因为中框楼盖梁的b′f较大,c较小;中跨楼盖梁的εt较边跨小,这是因为中跨楼盖梁轴压力较大,c较大;底筋配筋率ρ越大,εt越小。在跨中混凝土受压区保护层剥落后,由于c增大,εt以较大的斜率减小。
楼盖梁和简支梁的εb均随挠度Δ增大而近似线性增大,二者相差不大。空间位置对εb的影响并不显著,可能是由于εb的测量值在大于屈服应变时精度较低,微小的差别无法在测量结果中体现。ρ越大,εb越小。测量底筋拉应变的应变片在εb较大时失真,因此,仅给出加载前期一部分的应变曲线。
2.5 板钢筋应变选取板B说明X向板筋应变的发展规律,如图 11所示(板B的Y向中部为0 mm,南侧为负,北侧为正)。对于西侧和东侧截面,由于梁上部架立筋不伸入支座,板筋在加载初期就开始受拉,在挠度较小(5 mm)时,板端部形成了贯通的X向裂缝,板南北侧靠近楼盖梁的板筋达到屈服应变;在挠度达到15 mm时,全截面板筋均已屈服。

|
图 11 板B板筋应变 Fig. 11 Bar strain of slab B |
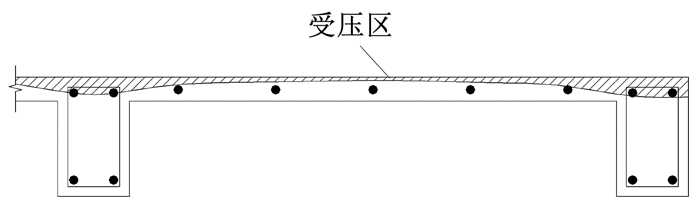
对于中部截面,在挠度10 mm前,应变较小(小于0.3×10-3),梁底筋屈服后,板筋受拉且应变逐渐增大,板中部应变大于近梁侧应变。可知跨中截面梁板的混凝土受压区高度是不均匀分布的,在梁上部最大,板中部最小,如图 12所示。
|
图 12 跨中受压区示意 Fig. 12 Schematic diagrams of compression zone in mid-span |
以P-Δ曲线的峰值荷载作为试验梁承载力Ptest,结果如图 13(a)所示。各国规范均基于平截面假定计算RC梁截面受弯承载力,结果相差不大[21],但都未考虑钢筋硬化及套箍效应[22]对材料强度的提高,而截面分析方法可以考虑这些材料因素的影响。采用截面分析方法和塑性铰理论,按无轴力的受弯构件计算试验梁承载力P0,并计算试验承载力与受弯构件承载力的比值Ptest/P0,结果如图 13(b)所示。计算P0时,对于支座截面,梁上部架立筋不发挥受拉作用(架立筋不伸入支座),受拉纵筋取相邻板一半板宽范围内的X向板筋;跨中截面有效翼缘宽度b′f按混凝土规范[5]5.2.4确定,对于中框梁为1 000 mm,对于边框梁为500 mm。

|
图 13 Ptest、Ptest/P0与ρ的关系 Fig. 13 Relationships between Ptest, Ptest/P0 and ρ |
由图 13可知,在ρ相同时,不同空间位置的楼盖梁Ptest大小关系为:边框边跨 < 边框中跨 < 中框边跨 < 中框中跨。如表 7所示,中框楼盖梁承载力较相应边框楼盖梁平均提高29%,中跨楼盖梁承载力较相应边跨楼盖梁平均提高18%。中框楼盖梁为T形截面,较边框楼盖梁的倒L形截面有更多的楼板参与受力。中跨楼盖梁的轴向约束刚度大于边跨楼盖梁。楼盖梁Ptest随ρ的增大而增大,但Ptest/P0随ρ的增大而减小。Ptest/P0范围为1.57~2.77,平均值为1.96。
| 表 7 梁试件承载力对比 Tab. 7 Comparison of capacity of beam specimens |
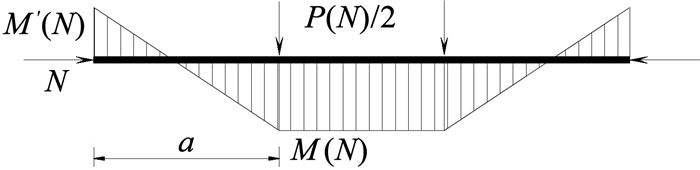
将楼盖梁视为压弯构件,假定轴力沿梁长保持不变,支座截面和跨中截面同时达到压弯承载能力极限状态,如图 14所示,得峰值承载力P与轴力N的关系式:
| $P(N)=2\left[M(N)+M^{\prime}(N)\right] /a$ | (1) |
|
图 14 楼盖梁弯矩图 Fig. 14 Flexural moment diagram of floor beam |
式中:M(N)、M′(N)分别为跨中、支座截面偏心受压下的受弯承载力,可由截面N-M分析得到。a为加载点距支座的距离,本文为900 mm。
在楼盖梁达到荷载峰值时,楼板支座截面X向板筋起到了受拉纵筋的作用,全截面板筋均已屈服;跨中截面受拉底筋也已屈服。因此,支座截面和跨中截面都处于大偏压极限状态,P与N为单调关系,可根据楼盖梁的试验峰值荷载Ptest确定与之对应的荷载峰值点的楼盖梁计算轴力Nc,进而根据Nc确定荷载峰值点的跨中弯矩Mc和支座弯矩M′c。楼盖梁跨中弯矩分析流程如图 15所示,计算M(N)时,b′f按规范确定;计算M′(N)时,受拉纵筋取相邻板X向板筋面积的一半;弯矩取矩点为0.5倍截面高度处[23]。计算结果如表 8所示,并计算Mc/M0,结果如图 16所示。Mc/M0的范围为1.28~2.19,不同空间位置楼盖梁的Mc/M0不同,同一空间位置楼盖梁的Mc/M0随ρ增大而减小,与Ptest/P0的规律一致。

|
图 15 楼盖梁跨中弯矩分析流程 Fig. 15 Analysis process of mid-span moment of floor beam specimens |
| 表 8 楼盖梁跨中弯矩的分析结果 Tab. 8 Analysis results of mid-span moment of floor beam specimens |

|
图 16 Mc/M0与ρ的关系 Fig. 16 Relationships between Mc/M0 and ρ |
采用OpenSees平台建立试验结构的有限元模型,梁、柱采用基于刚度法的纤维单元,试验层板采用分层壳单元。采用刚性杆模拟试验梁端部节点刚域。将试验梁纤维截面的参考轴设置在距梁顶30 mm(hf/2)处以考虑梁板偏心距的影响。由于柱脚平放于试验场地上,不约束柱脚节点的水平平动。纤维截面混凝土本构选用Concrete02,分层壳截面混凝土本构选用PlasticDamageConcretePlaneStress。钢筋本构选用ReinforcingSteel。模型如图 17所示。

|
图 17 有限元模型 Fig. 17 Finite element model |
楼盖梁试验与模拟的荷载-挠度曲线对比见图 18,轴向伸长对比见图 19。模拟所得的加载荷载偏小,荷载峰值点挠度偏大,但总体上,有限元模型计算结果与试验结果吻合较好,能较好地模拟楼盖梁的承载力等宏观响应。

|
图 18 试验与有限元模拟荷载-挠度曲线对比 Fig. 18 Comparison of load-deflection curve between test and finite element simulation |

|
图 19 试验与有限元模拟轴向伸长对比 Fig. 19 Comparison of elongation between test and finite element simulation |
楼盖梁截面包含不同宽度楼板时的沿梁跨轴力分布见图 20。图例为“楼盖梁试件编号_楼盖梁矩形截面中线距翼缘端部的距离df”,对于中框楼盖梁,df=b′f/2,对于边框楼盖梁,df=b′f-b/2。df=90 mm相当于矩形截面,df=700 mm相当于翼缘取相邻板的一半。横坐标x为距楼盖梁左端的距离。轴力以受压为正。轴力提取时刻的挠度为30 mm,对于试验与模拟,挠度取30 mm时的荷载均已接近峰值荷载。楼盖梁矩形截面内轴力在端部最大,在跨中受拉,因为跨中楼板翼缘承受了较大的轴压力。随着df的增大,楼盖梁轴力沿梁跨分布趋于均匀。

|
图 20 楼盖梁轴力分布 Fig. 20 Axial force distribution of floor beam |
df=700 mm时的轴力-轴向伸长曲线见图 21。为验证3.2节分析方法的合理性,将各楼盖梁的(dh, p, Nc)绘于图 21中并与模拟曲线对比(dh, p为试验荷载峰值点的轴向伸长)。由于混凝土强度的离散性及分析方法假定带来的误差,分析结果数据点与模拟曲线存在一定误差,但误差不大,Nc满足分析的需求。

|
图 21 轴力-轴向伸长曲线与(dh,p, Nc) Fig. 21 Comparison between (dh,p, Nc) and axial force-elongation curve |
考虑结构空间约束的楼盖梁在竖向受荷时,可将其视为带翼缘的压弯构件。空间位置对楼盖梁的影响体现在楼板翼缘和轴向约束刚度上。中框楼盖梁两侧有板,边框楼盖梁一侧有板。由图 21可知,中跨楼盖梁的轴向约束刚度大于边跨楼盖梁,中框楼盖梁的轴向约束刚度略大于边框楼盖梁。T形截面的中框楼盖梁的自由轴向伸长大于倒L形截面的边框楼盖梁,但由于相邻榀框架的协同变形,两者的约束轴向伸长趋于相等,因此,中框楼盖梁受到了边框架的额外轴向约束,边框楼盖梁的轴向约束受到削弱。
5 结论1) 楼盖梁受到随挠度增大而增大的轴向压力,属于压弯构件,不是目前规范定义的受弯构件。轴向压力导致楼盖梁承载力大幅提高、延性降低。
2) 楼盖梁跨中截面处于大偏压受力状态,破坏形态符合适筋梁弯曲破坏的特征。
3) 楼盖梁试件承载力与按受弯状态计算承载力之比平均值为1.96,范围为1.57~2.77,并与底筋配筋率成反比。楼盖梁试件与相应矩形简支梁试件承载力之比平均值为2.74,范围为1.80~4.20,与相应T形简支梁试件承载力之比平均值为2.57,范围为1.76~3.58。楼盖梁承载力与其所处空间位置有关,中框楼盖梁试件承载力比边框楼盖梁试件平均增大29%,中跨楼盖梁试件承载力比边跨楼盖梁试件平均增大18%。
4) 通过分析得到与试验峰值荷载对应的楼盖梁试件轴力和弯矩,跨中截面压弯状态弯矩与受弯状态弯矩的比值范围为1.28~2.19。
5) 随着楼盖梁截面包含的楼板范围增大,楼盖梁轴力沿梁跨分布趋于均匀。
| [1] |
VALIPOUR H, FARHANGVESALI N, FOSTER S. A generic model for investigation of arching action in reinforced concrete members[J]. Construction and Building Materials, 2013, 38: 742. DOI:10.1016/j.conbuildmat.2012.09.046 |
| [2] |
徐平辉. 竖向荷载作用下现浇楼板对梁抗弯承载力影响的试验与研究[D]. 广州: 华南理工大学, 2007: 20 XU Pinghui. Experimental study on the influence of casting slab upon the flexural strength of beam under vertical load[D]. Guangzhou: South China University of Technology, 2007: 20 |
| [3] |
江化冰. 重力荷载作用下普通梁带次梁整浇钢筋混凝土楼盖弹塑性受力分析与试验研究[D]. 深圳: 深圳大学, 2006: 38 JIANG Huabing. Nonlinear analysis and experiment research of the cast-in-situ RC main-beam with sub-beam deck under gravity loads[D]. Shenzhen: Shenzhen University, 2006: 38 |
| [4] |
韩小雷, 郑振光, 梁晓敏, 等. 考虑结构空间约束的现浇楼盖梁受剪性能试验研究[J]. 土木工程学报, 2023, 56(11): 16. HAN Xiaolei, ZHENG Zhenguang, LIANG Xiaomin, et al. The study on shear behavior of cast-in-situ floor beams considering structural spatial restraint[J]. China Civil Engineering Journal, 2023, 56(11): 16. DOI:10.15951/j.tmgcxb.22060595 |
| [5] |
中国建筑科学研究院. 混凝土结构设计规范: GB 50010—2010[S]. 北京: 中国建筑工业出版社, 2010 China Academy of Building Research. Code for design of concrete structures: GB 50010—2010[S]. Beijing: China Architecture & Building Press, 2010 |
| [6] |
ACI 318 Committee. Building code requirements for structural concrete (ACI 318-14) and commentary (ACI 318R-14)[S]. Farmington Hills, MI: American Concrete Institute, 2014
|
| [7] |
国家建委建筑科学研究院. 钢筋混凝土结构研究报告选集[M]. 北京: 中国建筑工业出版社, 1977: 104. Institute of Building Science of the State Construction Committee. Selected research reports on reinforced concrete structures[M]. Beijing: China Construction Industry Press, 1977: 104. |
| [8] |
OCKLESTON A. Load tests on a three storey reinforced concrete building in Johannesburg[J]. The Structural Engineer, 1955, 33: 304. |
| [9] |
OCKLESTON A J. Arching action in reinforced concrete slabs[J]. Structural Engineer, 1958, 36(6): 197. |
| [10] |
易伟建, 何庆锋, 肖岩. 钢筋混凝土框架结构抗倒塌性能的试验研究[J]. 建筑结构学报, 2007, 28(5): 104. YI Weijian, HE Qingfeng, XIAO Yan. Collapse performance of RC frame structure[J]. Journal of Building Structures, 2007, 28(5): 104. DOI:10.14006/j.jzjgxb.2007.05.013 |
| [11] |
GU Xianglin, ZHANG Bin, WANG Ying, et al. Experimental investigation and numerical simulation on progressive collapse resistance of RC frame structures considering beam flange effects[J]. Journal of Building Engineering, 2021, 42: 1. DOI:10.1016/j.jobe.2021.102797 |
| [12] |
陈明辉, 宋晓胜, 苏幼坡. 配筋率对钢筋混凝土框架梁极限承载力的影响: 拱效应试验研究[J]. 自然灾害学报, 2010, 19(1): 44. CHEN Minghui, SONG Xiaosheng, SU Youpo. Influence of reinforcement ratio on ultimate bearing capacity of reinforced concrete frame beams: test study on arch action[J]. Journal of Natural Disasters, 2010, 19(1): 44. DOI:10.13577/j.jnd.2010.0108 |
| [13] |
SU Youpo, TIAN Ying, SONG Xiaosheng. Progressive collapse resistance of axially-restrained frame beams[J]. ACI Structural Journal, 2009, 106(5): 600. DOI:10.14359/51663100 |
| [14] |
RUDDLE M E, RANKIN G I B, LONG A E. Arching action: flexural and shear strength enhancements in rectangular and Tee beams[J]. Proceedings of the Institution of Civil Engineers-Structures and Buildings, 2003, 156(1): 63. DOI:10.1680/stbu.2003.156.1.63 |
| [15] |
RUDDLE M E. Arching action and the ultimate capacity of reinforced concrete beams[D]. Belfast: Queen's University Belfast, 1989: 56
|
| [16] |
FARHANGVESALI N, VALIPOUR H, SAMALI B, et al. Development of arching action in longitudinally-restrained reinforced concrete beams[J]. Construction and Building Materials, 2013, 47: 7. DOI:10.1016/j.conbuildmat.2013.04.050 |
| [17] |
黄狄昉. 考虑结构空间约束的钢筋混凝土框架结构抗震性能研究[D]. 广州: 华南理工大学, 2022: 120 HUANG Difang. Seismic performance of reinforced concrete frames considering structural spatial constraint effect[D]. Guangzhou: South China University of Technology, 2022: 120 |
| [18] |
蒋利学, 郑乔文. 竖向荷载作用下整浇梁板的空间效应试验研究[J]. 建筑结构学报, 2009, 30(增刊1): 200. JIANG Lixue, ZHENG Qiaowen. Experimental research on spatial effect of cast-in-situ beam-slab system under vertical loads[J]. Journal of Building Structures, 2009, 30(Sup.1): 200. DOI:10.14006/j.jzjgxb.2009.s1.037 |
| [19] |
NAAMAN A E, HARAJLI M H, WIGHT J K. Analysis of ductility in partially prestressed concrete flexural members[J]. PCI Journal, 1986, 31(3): 64. DOI:10.15554/pcij.05011986.64.87 |
| [20] |
PARK R, FALCONER T. Ductility of prestressed concrete piles subjected to simulated seismic loading[J]. PCI Journal, 1983, 28(5): 112. DOI:10.15554/pcij.09011983.112.144 |
| [21] |
肖良丽, 潘明杨. 中、美、欧混凝土梁的受弯性能对比研究[J]. 工程建设与设计, 2012(10): 73. XIAO Liangli, PAN Mingyang. Comparative study on the flexural behavior of concrete beams in the United States and European[J]. Architectural and Structural Design, 2012(10): 73. |
| [22] |
钱稼茹, 程丽荣, 周栋梁. 普通箍筋约束混凝土柱的中心受压性能[J]. 清华大学学报(自然科学版), 2002, 42(10): 1369. QIAN Jiaru, CHENG Lirong, ZHOU Dongliang. Behavior of axially loaded concrete columns confined with ordinary hoops[J]. Journal of Tsinghua University (Science and Technology), 2002, 42(10): 1369. DOI:10.16511/j.cnki.qhdxxb.2002.10.024 |
| [23] |
LU Xinzheng, LIN Kaiqi, LI Chenfeng, et al. New analytical calculation models for compressive arch action in reinforced concrete structures[J]. Engineering Structures, 2018, 168: 721. DOI:10.1016/j.engstruct.2018.04.097 |
 2024, Vol. 56
2024, Vol. 56



 22
22 10@100(3)
10@100(3) 16; 2
16; 2 16
16 6@150(2)
6@150(2) 22; 4
22; 4 22
22 10@100(2)
10@100(2) 22
22 22+1
22+1 16
16 22+1
22+1 16
16 22
22 22+1
22+1 16
16 22+1
22+1 16
16 16
16 16
16 22
22 16
16 16
16 22
22 22+1
22+1 16
16 16
16 22+1
22+1 16
16 16
16