2. 中国空气动力研究与发展中心 超高速空气动力研究所, 四川 绵阳 621000
2. China Aerodynamics Research & Development Center, Hypervelocity Aerodynamics Institute, Mianyang 621000, China
硬件演化(evolvable hardware, EHW)技术在上世纪90年代已被提出,其具有的自组织、自适应和自修复能力在电路故障修复领域发挥了重要作用[1-4].目前常将现场可编程门阵列(field programming gate array, FPGA)作为实现EHW的硬件基础,但由于FPGA生产商均为外企,对外实行技术封锁,除Xilinx的Virtex2系列芯片外,学者不能够自由的访问/控制FPGA内部逻辑单元和开关盒[5-8],对EHW技术的发展造成一定影响.因此虚拟可重构电路(virtual reconfigurable circuits, VRC)应运而生[9-11],其能够克服以上问题.
VRC与故障自修复领域中的胚胎电子细胞都是可编程阵列[12-14],因而具有相似性;由于可编程单元(programmable elements, PE)内部结构和PE间互联不同,又具有差异性.虽然现有伪穷举测试法、布尔差分法、D算法等故障定位方法[15-17],但都针对具体电路,需输入测试序列.而VRC结构具有特殊性,使得数字电路常用测试方法不适用.常规的VRC故障定位方法主要进行逐行(列)测试,且需对PE的所有逻辑功能进行测试,因此VRC的行(列)数决定了测试的次数,容易造成测试次数大等问题.一些文献提出将可能存在故障的行(列)所有PE单独连接至无故障的行(列)进行测试,在故障可能存在的行(列)较少时,且无故障行(列)较多和每行(列)的PE数量较少时才使用,否则将无足够无故障行(列)供使用[18].另有很多文献只研究VRC的使用,而回避VRC故障定位[9-10, 19].
本文提出一种基于改进二分查找的VRC快速故障定位技术.首先采用一次行测试和一次列测试确定故障可疑区域,然后根据故障可疑区域的规模确定测试方向,最后采用二分查找技术对故障可疑区域进行故障定位.通过对本文提出的故障定位方法进行性能分析,所提方法的可行性和有效性得到验证.
1 VRC平台基本原理EHW技术主要有内部演化(intrinsic EHW)和外部演化(extrinsic EHW)两种方式.而基于VRC的电路演化平台,也包含内部演化和外部演化两种演化方式[1, 2, 4, 20].
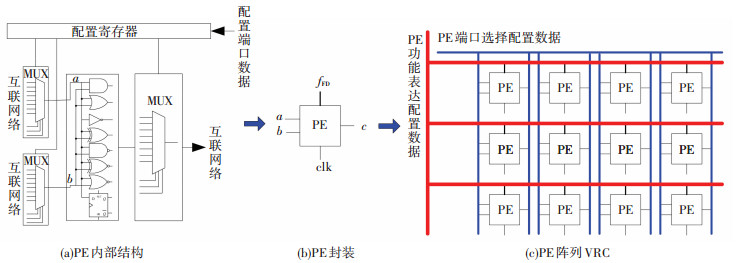
VRC是一种基于FPGA中可编程逻辑单元重新封装后的可重构平台[9-11, 19],是由多个PE构成阵列,也称PE为function elements(FE)[9].每个PE可实现任意二输入逻辑功能,其中包括与、或、非、异或、与或、同或、与非、或非、D触发器共8种逻辑.有些文献设计的PE只包含8种逻辑中的部分逻辑. VRC构成示意见图 1.
|
图 1 VRC构成示意 Figure 1 Sketch diagram of VRC configuration |
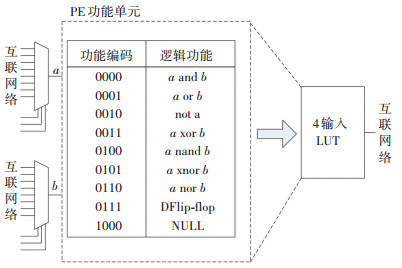
图 1中的a和b为输入信号,c为输出信号,fFD为PE功能表达配置数据,clk为时钟. VRC平台中的PE还可具有图 2所示结构[19],同图 1(a)中的PE结构具备相同功能. PE互联网络示意见图 3.
|
图 2 另一种PE内部结构示意 Figure 2 Sketch diagram of other kind of PE structure |
|
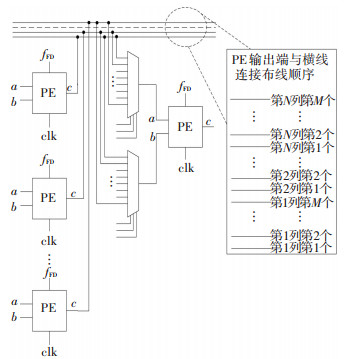
图 3 VRC互联网络示意 Figure 3 Interconnection network sketch diagram of VRC |
从图 3可看出,针对规模为M行N列的VRC,每个PE的输出端均互联至整个VRC,每个PE的每个输入端均有一个M×N到一的多路选择器(multiplexer, MUX),将所有PE输出端连接至具有M×N个输入一个输出的MUX,使得VRC中每个PE输出端能够接入任意PE的输入端.
对MUX的M×N个输入端进行二进制计算,对应的位数为所有MUX控制信号的编码长度.假如M×N=60,其二进制编码为111 100,控制MUX的信号编码长度为6位.
2 基于改进二分查找的VRC快速故障定位技术本文提出的基于改进二分查找的VRC快速故障定位技术的主要原理如下:首先实施一次行测试和一次列测试确定故障可疑区域,再采用二分查找技术对故障可疑区域进行故障定位.
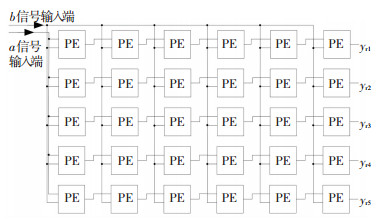
对VRC实施行/列测试的PE连接/配置方法分别见图 4和图 5.
|
图 4 VRC行测试配置方法 Figure 4 Row-test configuration method of VRC |
|
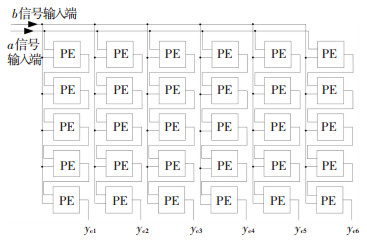
图 5 VRC列测试配置方法 Figure 5 Column-test configuration method of VRC |
图 4和图 5中的yr1~yr5和yc1~yc6分别对应行测试和列测试的每路输出信号.行/列测试时通过改变输入端a和b的值,保证每个PE能将逻辑1顺利输出到端口.比如在测试PE的逻辑“与”功能时,输入信号a和b需同时输入1,或同时输入0.如果输入1时输出为1,且输入0时输出为0,代表无故障,反之则有故障.将经过行测试和列测试后的交叉区域记为故障PE可疑区域见图 6.

|
图 6 VRC故障PE可疑区域 Figure 6 Fault PE shadiness area of VRC |
经过行测试后,确定第2~4行存在故障;经过列测试后,确定第2~5列存在故障.此时的故障可疑区域不只一行和一列.
在基于行测试、列测试和故障可疑区域基础之上,基于改进二分查找的VRC快速故障定位技术实现流程如下:
Step 1 首先进行行测试和列测试,确定故障可疑区域.
Step 2 判断VRC故障可疑区域的大小,假设可疑区域规模为m行n列,且m≤n.判断VRC不在可疑区域内的PE(即无故障PE)数量k,如果k≥n,转入Step3;反之,则转入Step6.
Step 3 采用二分查找法,将可疑区域每一列平分(偶数直接平分,奇数平分时一边可多一个PE),分别按图 5方式纵向连接,并将两路信号送入此列无故障PE进行“与”操作.如果此列没有无故障PE,则选择其它列多余的无故障PE进行“与”操作.如果输出值为1,判定上/下两部分均存在故障,并转入Step4;如果输出值为0,判断上/下部分中有一部分存在故障,并转入Step5.
Step 4 当平分后的上/下两部分均存在故障时,对上部分进行再次平分,按照Step3的步骤进行故障定位.在上部分故障定位完毕后,再对下部分故障定位.依此进行,直到可疑区域的故障完全定位为止.
Step 5 当平分后的上/下两部分只有一部分存在故障时,首先测试上/下部分的任意部分.如果测试出上部分(下部分)无故障,则下部分(上部分)必存在故障,此时测试次数将大大缩减.
Step 6 在Step2中确定可疑区域后,当k<n时,需逐行精确测试;当测试后k ≥ n时,按照Step3、Step4和Step5的流程进行故障定位.
在上述测试流程中,如果VRC中故障PE只存在某一行或某一列,只需一次行测试和一次列测试即可定位故障.详细的二分法查找过程见图 7.
|
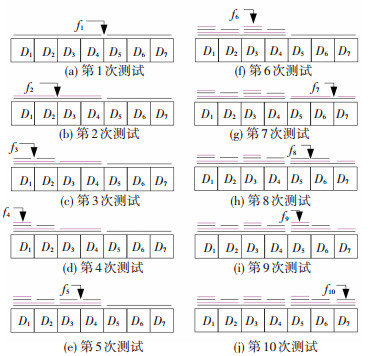
图 7 极端情形下二分查找故障定位过程 Figure 7 Binary search process of fault localization under extreme circumstances |
图 7所示测试步骤包含极端情形下的测试次数,将可疑区域中的某一行分离出来单独演示,包含7个PE,分别用字母D1 ~ D7表示,测试点用f1~f10表示.在非极端情形下,图 7中一些测试步骤可省略.此时的极端情形主要指:在二分过程中且还未最小二分时,两侧测试始终显示有故障;在最小二分时,两侧测试显示无故障.
图 7中f1、f2属于中间过程的二分,而f3、f5、f7和f8属于最小二分,且以上均属于节点测试,f4、f6、f9和f10属于逻辑块功能测试. 图 7中只要D7无故障,且D1和D2、D3和D4、D5和D6每对中只要有一个故障,将造成最大测试次数.即至少存在4个故障PE,相当于至少4/7的PE出现故障,而4/7的PE出现故障的概率极小.
3 故障定位性能分析故障定位性能分析,主要关注故障全部定位情况下的测试次数,通常情况下,测试次数越少越好.常规测试方法需进行逐行(或逐列)测试.在对比分析中,设定测试顺序从上至下(从左至右).针对VRC规模为M行N列,且M ≤ N,常规的故障定位方法最大测试次数为M次.本文提出的基于改进二分查找的VRC快速定位技术,在极端情形下的最大测试次数为G(x),其中x代表图 6中故障可疑区域的行数和列数的最小值,不是VRC中故障PE的数量(用h表示,h∈N+).
在故障定位过程中,确定故障可疑区域需要测试两次.当PE数量取2的对数为整数时(即PE数量等于2x,x∈N+),极端情形下需测试分界点,x个PE有x-1个分界点,需测试x-1次.当两个PE为一组时,x个PE最后细分为0.5x等分.对每个等分进行故障确认需测试1次,测试次数合计为1.5x+1.在x个PE基础上,每增加1个PE,测试次数将增加两次(1次分界点测试,1次确认测试);在x个PE基础上增加的PE数量多余0.5x时,每增加1个PE将增加1次测试(分界点测试).因此,G(x)为
| $ \begin{array}{l} G\left( x \right) = \\ \left\{ \begin{array}{l} 1.5 \times {2^{\left\lfloor {{\rm{lo}}{{\rm{g}}_2}x} \right\rfloor }} + 1 + 2 \times (x - {2^{\left\lfloor {{\rm{lo}}{{\rm{g}}_2}x} \right\rfloor }})\\ 1.5 \times {2^{\left\lfloor {{\rm{lo}}{{\rm{g}}_2}x} \right\rfloor }} + 1 + {2^{\left\lfloor {{\rm{lo}}{{\rm{g}}_2}x} \right\rfloor }} + \left[{\left( {x-{2^{\left\lfloor {{\rm{lo}}{{\rm{g}}_2}x} \right\rfloor }}} \right)-{2^{\left\lfloor {{\rm{lo}}{{\rm{g}}_2}x} \right\rfloor-1}}} \right] \end{array} \right.{\rm{ = }}\\ \left\{ \begin{array}{l} {\rm{ - }}{2^{\left\lfloor {{\rm{lo}}{{\rm{g}}_2}x} \right\rfloor-1 }} + 2x + 1, {\rm{ }}x{\rm{ - }}{2^{\left\lfloor {{\rm{lo}}{{\rm{g}}_2}x} \right\rfloor }} \le {2^{\left\lfloor {{\rm{lo}}{{\rm{g}}_2}x} \right\rfloor-1 }}, x \in {N^ + };\\ {2^{\left\lfloor {{\rm{lo}}{{\rm{g}}_2}x} \right\rfloor }} + x + 1, {\rm{ }}x - {2^{\left\lfloor {{\rm{lo}}{{\rm{g}}_2}x} \right\rfloor }} > {2^{\left\lfloor {{\rm{lo}}{{\rm{g}}_2}x} \right\rfloor-1 }}, x \in {N^ + }. \end{array} \right. \end{array} $ | (1) |
相比传统的故障定位方法,虽然本文提出的故障定位技术在极端情形下的测试次数最大增加约一半,但只存在于极端情况下,即整个VRC阵列均存在故障.在当VRC出现故障PE数量占VRC总PE数量≤50%时,本文提出的VRC快速故障定位技术将具有明显的优势.
由于VRC阵列PE的结构一样,因此出现故障概率也一样.假设一个PE出现故障的概率为p,则k个PE出现故障的概率服从二项分布,且为
| $ P\left( {X = k} \right) = b\left( {k;M \times N, p} \right) = C_{M \times N}^k{p^k}{\left( {1{\rm{ - }}p} \right)^{M \times N{\rm{ - }}k}}. $ | (2) |
式中: X为PE总数,λ为失效率,t为工作时间,p=1-e-λt.当λ=1×10-5、t=24×365、λ分别为3个不同失效率值、故障PE概率累积量大于99%时,h与X的比值为phX见图 8.
|
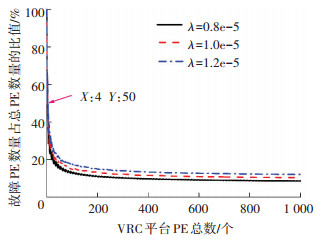
图 8 概率累积量大于99%时故障PE数量占总数量百分比 Figure 8 Ratio of the number of fault PE of total number when probability cumulant is larger than 99% |
图 8中,随着VRC规模的增大,无论λ是0.8×10-5、1.0×10-5还是1.2×10-5,phX始终呈下降趋势,且慢慢趋于稳定.当X≤4时,故障PE数量占总PE数量的百分比才会超过50%.
当X<4时,PE只能排成一行或一列,采用本文提出的故障定位技术,只需两次测试.当X=4时,如果4个PE排成一行或一列,只需两次测试.但如果4个PE呈两行两列的阵列排列时,取消可疑区域测试,只进行二分查找测试,需测试两次.当X>4时,X越大,不到50%的PE存在故障的概率为0.99,当VRC规模大于200个时,少于20%的PE存在故障的概率为0.99.此时,本文提出的故障快速定位技术将具有明显优势.
对于规模为10×10的VRC,只有当h>14时,且在特定故障布局下,才可能造成最大测试次数,见图 9.
|
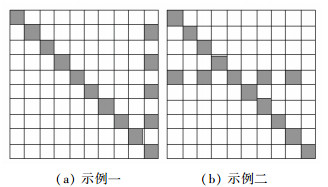
图 9 可造成最大测试次数的故障PE分布 Figure 9 Fault PE distribution map under max test times |
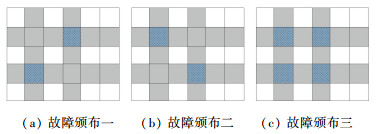
图 9中只给出了两种故障PE分布示意图.其中,深色方块代表故障PE,白色方块代表无故障PE.造成最大测试次数的必要条件如下:一是有一列或一行中每隔一个PE必须存在故障,而间隔中的PE可有故障也可无故障.二是除开当前列(行),剩余的故障PE不能出现在同一行或同一列. 图 10展示了不同h值造成相同故障可疑区域的示例.
|
图 10 不同h值造成相同故障可疑区域示例 Figure 10 Instances of the same fault PE shadiness area under different value of h |
造成最大测试次数单独列出现的最少故障数量为H(x)
| $ H\left( x \right) = \left\{ \begin{array}{l} {2^{\left\lfloor {{\rm{lo}}{{\rm{g}}_2}x} \right\rfloor {\rm{ - }}1}}, {\rm{ }}x{\rm{ - }}{2^{\left\lfloor {{\rm{lo}}{{\rm{g}}_2}x} \right\rfloor }} \le {2^{\left\lfloor {{\rm{lo}}{{\rm{g}}_2}x} \right\rfloor {\rm{ - }}1}}, x \in {N^ + };\\ x{\rm{ - }}{2^{\left\lfloor {{\rm{lo}}{{\rm{g}}_2}x} \right\rfloor }}, {\rm{ }}x{\rm{ - }}{2^{\left\lfloor {{\rm{lo}}{{\rm{g}}_2}x} \right\rfloor }} > {2^{\left\lfloor {{\rm{lo}}{{\rm{g}}_2}x} \right\rfloor {\rm{ - }}1}}, x \in {N^ + }. \end{array} \right. $ | (3) |
造成最大测试次数的可疑区域最小h值用为H1(x)
| $ {H_1}\left( x \right) = H\left( x \right) + x{\rm{ - }}1\;\;x \in {N^ + }. $ | (4) |
深入研究规模为10×10的VRC,采用常规方法进行故障定位,当从上至下定位时,只要最后一行出现故障,将造成最大测试次数.对应不同h值造成最大测试次数的概率用P1(x)为
| $ {P_1}\left( x \right) = \left\{ \begin{array}{l} 1{\rm{ - }}\frac{{C_{90}^x}}{{C_{100}^x}}, {\rm{ }}x \le 90, x \in {N^ + };\\ 1, {\rm{ }}91 \le x \le 100, x \in {N^ + }. \end{array} \right. $ | (5) |
在采用本文提出的方法时,按照式(3)和式(4)的计算规则,故障PE可疑区域为10×10的最小h =13.其不同h值造成最大测试次数的概率为P2(x)
| $ {P_2}\left( x \right) = \left\{ \begin{array}{l} \frac{{{{\left( {10!} \right)}^2}}}{{{{\left( {\left( {10{\rm{ - }}x} \right)!} \right)}^2} \times \left( {x!} \right) \times C_{100}^x}},\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;x \le 10,x \in {N^ + };\\ \frac{{1\left( {10!} \right) \times {2^{x{\rm{ - }}6}}}}{{C_{100}^x}},{\rm{ }}x \in \left\{ {11,13} \right\};\\ \frac{{\left( {10!} \right) \times 128}}{{C_{100}^x}},{\rm{ }}x = 12;\\ {P_3}\left( x \right),{\rm{ }}x \ge 14,x \in {N^ + }. \end{array} \right. $ | (6) |
式(6)中的P3(x)可表示为
| $ {P_3}\left( x \right) \le \frac{{\left( {10!} \right) \times 128 \times C_{81}^{x{\rm{ - }}13}}}{{C_{100}^x}}, {\rm{ }}x \ge 14, x \in {N^ + }. $ | (7) |
从式(6)、(7)可看出,当x∈[1,13], x∈N+时,式(6)属于精确计算,当x≥14, x∈N+时,式(6)属于近似范围计算.当计算的近似值比真值大时,造成最大测试次数概率远远低于常规方法造成最大测试次数的概率.
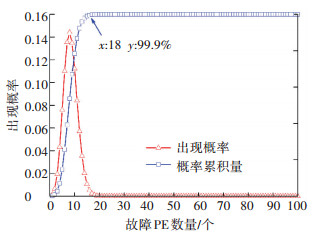
令每个PE的失效率λ=1.0×10-5,t= 24×365,VRC不同数量PE出现故障的概率和对应的概率累积量见图 11.
|
图 11 VRC不同数量故障PE故障出现概率及概率累积量 Figure 11 Fault probability and fault probability cumulant of VRC in different number of PEs |
从图 11中可看出,当VRC的故障PE概率累积量达到99.9%时,对应有min(h)=18.因此只计算最多18个PE出现故障,故障定位相关参数见表 1,表 1中造成最大测试次数的故障分布和故障随机分布的比率用S表.
| 表 1 VRC阵列(规模为10×10)故障定位相关参数 Table 1 Related parameters of VRC fault localization (scale is 10×10) |
从表 1可看出,常规故障定位方法最大测试次数始终为10次.本文提出的故障定位方法最大测试次数,在h<7时明显低于前者.当h≥7时大于前者,最大增加量约为一半.但本文提出的方法造成最大测试次数的故障PE需特殊布局,且相同数量故障PE特殊布局所出现的概率.在h=7时,常规方法是本文提出方法的118倍;h=10时是3.19×106倍;h=13是2.34×107倍;即使在近似计算h=18时,前者也为后者的5.03×103倍.
当h值确定时,常规故障定位方法始终有S=0.1.采用本文提出的方法,当h≤6时,虽然S>0.1,但是此时的最大测试次数小于常规方法的测试次数.当h>6时,虽然最大测试次数大于常规测试方法,但此时S远小于0.1,之间差距从40倍到3.06×106倍不等.
排除极端情形下造成最大测试次数,当实例中h≤6时,只要VRC最后一行存在故障PE,常规方法的测试次数大于本文提出的方法.如果7个故障PE全在第一行,本文提出的故障定位方法将需两次测试,而常规方法只需一次测试,但是7个故障全在第一行的概率只有7.50×10-8.当h>6时,需根据具体的故障PE分布分析故障测试次数.常规方法存在10%造成最大次数的概率,虽然本文提出的方法存在最大测试次数大于常规方法的可能性,但其概率低于1.94×10-4,甚至更小.
例如,当VRC阵列只有1个故障时,常规方法检测次数少于两次的概率为20%,即80%的检测次数都大于2次.而采用本文提出的方法,测试次数只使用两次.对于双故障,常规方法93.03%的检测次数大于4次.而采用本文提出方法的最大测试次数为4次(2次测试占3.64%,4次测试占96.36%).
当h=7时,如图 12所示的故障分布.由于每个故障分布在不同的行和列,常规测试方法需进行10次测试,才能将7个故障PE完全定位.而采用本文方法只需进行8次测试,中间3行连续分布的无故障PE得到快速隔离.

|
图 12 VRC中7个故障PE分布 Figure 12 Seven fault PEs distribution diagram of VRC |
综上所述,故障定位的测试次数和故障PE的分布密切相关.常规故障定位方法,无论某行/列是否存在故障PE,均需要测试一次.本文提出的故障定位方法能够将无故障的行/列排除,只对故障可疑区域进行二分查找测试,从而降低故障测试次数.
4 结论针对目前VRC阵列故障定位方法单一、故障定位难及定位测试次数大等问题,本文提出一种基于改进二分查找的VRC快速故障定位技术.
和常规故障定位技术相比,本文提出的故障快速定位技术能够避免对连续分布的无故障PE进行测试,缩小测试区域,且造成最大测试次数的概率远小于前者,对单故障和双故障定位时的测试次数缩减量超过50%.
通过故障定位性能分析,本文提出的基于改进二分查找的VRC快速故障定位技术的可行性和有效性得到验证,具有一定通用性和工程应用价值.
| [1] |
PAULINE C H, ANDY M T. Challenges of evolvable hardware: past, present and the path to a promising future[J].
Genetic Programming and Evolvable Machines, 2011, 12(3): 183-215.
DOI: 10.1007/s10710-011-9141-6 |
| [2] |
HORNBY G S, LOHN J D, LINDEN D S. Computer-automated evolution of an x-band antenna for NASA's space technology 5 mission[J].
Evolutionary Computation, 2011, 19(1): 1-23.
DOI: 10.1162/EVCO_a_00005 |
| [3] |
HIHUCHI T, IWATA M, KAJITANI I, et al. Evolvable hardware and its applications to pattern recognition and fault tolerant systems[J].
Lecture Notes in Computer Science, 1996, 1062: 118-135.
DOI: 10.1007/3-540-61093-6 |
| [4] |
ZHANG Junbin, CAI Jinyan, MENG Yafeng, et al. Fault self-repair strategy based on evolvable hardware and reparation balance technology[J].
Chinese Journal of Aeronautics, 2014, 27(5): 1211-1222.
DOI: 10.1016/j.cja.2014.09.006 |
| [5] |
YAN S L, CHEN Y, PU Q M. A new evolutionary hardware system using FPGAS[C]//Proceeding of International Colloquium on Computing, Communication, Control, and Management. Piscataway, NJ: IEEE Press, 2009: 82-85.
|
| [6] |
LOPEZ-BUEDO S, GARRIDO J, BOEMO E I. Dynamically inserting, operating, and eliminating thermal sensors of FPGA-based systems[J].
IEEE Transactions on Components and Packing Technologies, 2002, 25(4): 561-566.
DOI: 10.1109/TCAPT.2002.808011 |
| [7] |
DAS N, ROY P, RAHAMAN H. Runtime congestion and crosstalk aware router for FPGA using jbits3.0 for partial reconfigurable[C]//Proceeding of International Symposium on Electronic System Design. Piscataway, NJ: IEEE Press, 2011: 146-151.
|
| [8] |
任小西, 李仁发, 金声震, 等. 基于JBits的一种可重构数据处理系统可靠性研究[J].
计算机研究与发展, 2007, 44(4): 722-728.
REN Xiaoxi, LI Renfa, JIN Shengzhen, et al. Research on reliability of a reconfigurable data processing system based on jbits[J]. Journal of Computer Research and Development, 2007, 44(4): 722-728. |
| [9] |
WANG Jin, LEE C H. Virtual reconfigurable architecture for evolving combinational logic circuits[J].
Journal of Central South University, 2014, 21(5): 1862-1870.
DOI: 10.1007/s11771-014-2132-z |
| [10] |
OMAR E, IMBABY I M, MOHAMED K R, et al. Hardware implementation of virtual reconfigurable circuit for fault tolerant evolvable hardware system on FPGA[J].
American Journal of Engineering and Technology Research, 2015, 15(1): 2015.
|
| [11] |
朴昌浩, 王进, 孙志华, 等. 自适应变异比率控制在虚拟可重构结构中的应用[J].
高技术通讯, 2010, 20(4): 398-402.
PIAO Changhao, WANG Jin, SUN Zhihua, et al. Applying self-adaptive mutation rate control to virtual reconfigurable architecture[J]. Chinese High Technology Letters, 2010, 20(4): 398-402. |
| [12] |
蔡金燕, 朱赛, 孟亚峰. 一种新型的仿生电子细胞基因存储结构[J].
电子学报, 2016, 44(8): 1915-1924.
CAI Jinyan, ZHU Sai, MENG Yafeng. A novel gene memory structure for bio-inspired electronic cell[J]. Acta Electronica Sinica, 2016, 44(8): 1915-1924. |
| [13] |
王南天, 钱彦岭, 李岳, 等. 胚胎型在线自修复FIR滤波器研究[J].
仪器仪表学报, 2012, 33(6): 1385-1391.
WANG Nantian, QIAN Yanling, LI Yue, et al. Study of embryonic type on-line self-healing FIR filters[J]. Chinese Journal of Scientific Instrument, 2012, 33(6): 1385-1391. |
| [14] |
XU Guili, XIA Zhenghao, WANG Haibin, et al. Design of embryo-electronic systems capable of self-diagnosing and self-healing and configuration control[J].
Chinese Journal of Aeronautics, 2009, 22(6): 637-643.
DOI: 10.1016/S1000-9361(08)60152-1 |
| [15] |
朱敏, 王石记, 杨春玲. 改进Tent混沌序列的数字电路BIST技术[J].
哈尔滨工业大学学报, 2010, 42(4): 607-611.
ZHU Min, WANG Shiji, YANG Chunling. BIST technique of digital circuits based on improved tent chaotic sequence[J]. Journal of Harbin Institute of Technology, 2010, 42(4): 607-611. DOI: 10.11918/j.issn.0367-6234.2010.04.022 |
| [16] |
杨德才, 陈光䄔, 谢永乐. 进位保留阵列乘法器的一种内建自测试[J].
电子科技大学学报, 2007, 36(4): 751-754.
YANG Decai, CHEN Guangju, XIE Yongle. A built-in self-test scheme for carry save array multiplier[J]. Journal of University of Electronic Science and Technology of China, 2007, 36(4): 751-754. |
| [17] |
潘张鑫, 陈偕雄. 或-符合型通用逻辑门组合电路的故障检测[J].
浙江大学学报(工学版), 2007, 41(8): 1260-1264.
PAN Zhangxin, CHEN Xiexiong. Faults detection in combinational circuits of OR-coincidence type universal logic gates[J]. Journal of Zhejiang University (Engineering Science), 2007, 41(8): 1260-1264. |
| [18] |
娄建安, 崔新风, 褚杰. 基于类神经网络模型的电路自主修复方法[J].
军械工程学院学报, 2010, 22(6): 46-49.
LOU Jian'an, CUI Xinfeng, CHU Jie. Self-repairing method of the electronic circuit based on neural network model[J]. Journal of Ordnance Engineering College, 2010, 22(6): 46-49. |
| [19] |
张峻宾, 蔡金燕, 孟亚峰. 面向复杂电磁环境的容错电路系统设计技术[J].
西安交通大学学报, 2017, 51(2): 53-59.
ZHANG Junbin, CAI Jinyan, MENG Yafeng. A design technology of fault tolerance circuit systems facing complex electromagnetic environments[J]. Journal of Xi'an Jiaotong University, 2017, 51(2): 53-59. DOI: 10.7652/xjtuxb201702009 |
| [20] |
李杰, 黄士坦. 可进化硬件的动态进化[J].
武汉大学学报, 2008, 41(6): 103-107.
LI Jie, HUANG Shitan. Dynamic evolution for evolvable hardware[J]. Engineering Journal of Wuhan University, 2008, 41(6): 103-107. |
 2017, Vol. 49
2017, Vol. 49


