锁相环(Phased-Locked Loop,PLL)作为能够跟踪输入信号的相位反馈自动控制系统[1],其结构能用于实现对三相电压不平衡的补偿控制[2]和构造磁极位置检测电路[3];其控制方法可用于连续相位调制载波导航卫星信号的设计[4],因而受到广泛的研究.随着数字电路的发展,全数字锁相环(All Digital Phase-Locked Loop,ADPLL)由于具有可移植性强、配置灵活、设计周期短等优点,因此成为锁相环技术发展的重要趋势,能广泛用于全数字闭环角度解算算法设计[5]和基于全数字锁相环的激光通信PPM调制解调系统的设计[6].开发高性能的全数字锁相环是现代集成电路发展的迫切需求,且全数字锁相环电路中的时间数字转换器(Time-to-Digital Converter,TDC)结构是目前的研究热点之一[7].
时间数字转换器作为影响全数字锁相环性能优劣的重要电路,许多学者对TDC电路提出改进.文献[8]中传统的多时钟多相位TDC结构以消耗较多的硬件资源来保证动态范围,但存在量化精度低的问题.文献[9]中基于时间间隔放大器的分数指数型的TDC,使用级联的时间放大器放大相位差信号,因而分辨率具有一定的提高,但是环路的锁定时间较长.文献[10]中提出的基于自由环形振荡器的多相位型TDC,虽然能够有效改善电路的动态范围,但是量化脉冲信号的分辨率较低.文献[11]中设计的基于游标尺链型的TDC是利用两个分辨率比较接近的延时线对两路输入信号的时序进行比较和量化,在量化精度和硬件资源消耗上比传统的多时钟多相位TDC结构都有一定的改善,因而具有一定的代表性和优越性.
本文在文献[11]中TDC的基础上结合抽头延迟线法、双通道差分延迟线法、对称式层次型结构等手段,提出了一种三步对称式层次型时间数字转换器设计.该TDC将量化过程分为粗调、一级精调、二级精调三部分,分别对应采用计数器结构、抽头延迟线结构、双通道差分延迟线结构.在基于游标尺链型TDC的一级结构基础上扩展为三级对称式量化结构,提高了量化相位差的精度,解决了不能对负时间间隔量化的问题.将游标尺链型结构优化为双通道差分延迟线结构,缩短了游标尺链型结构的链路长度,降低了量化相位差的不确定度.同时,提出的相调电路通过状态机灵活调节反馈信号的低电平时间,在3个参考信号时钟周期内快速调整相位达到锁定状态.最后,在环路锁定后,采用下降沿检测电路适时关闭暂时不需要的电路,降低整体电路的功耗.
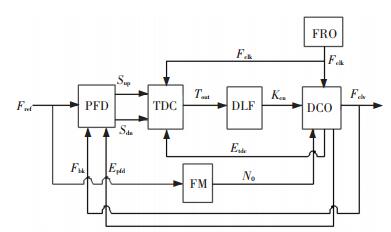
1 全数字锁相环整体电路设计 1.1 整体电路结构ADPLL的经典结构通常由鉴频鉴相器(Phase and Frequency Detector,PFD)、时间数字转换器(TDC)、数字环路滤波器(Digital Loop Filter,DLF)与数控振荡器(Digital Controlled Oscillator,DCO)等部分组成.本设计中的ADPLL原理框图见图 1,与经典结构相比较,增加了频率检测电路(Frequency Measurement,FM).整体电路的基本工作原理如下:首先FM电路量化参考信号Fref的频率,产生频率控制字N0,然后DCO根据N0值的大小进行分频,产生与参考信号同频但具有一定相位差的反馈信号Fbk,然后PFD比较参考信号与反馈信号的相位,输出相位差信号Sup和Sdn,相位差信号通过TDC量化后输出量化结果Tout,再经过DLF滤波后输出DCO的调节控制字Kcn,DCO中的相调电路根据调节控制字的大小调整反馈信号的相位,最终实现对参考信号的快速锁定.在环路锁定后,DCO中的下降沿检测电路适时将使能信号Epfd、Etdc置低,关闭PFD和TDC,降低环路的功耗.
|
图 1 ADPLL原理框图 Figure 1 Principle diagram of ADPLL |
鉴频鉴相器的作用是比较参考信号Fref与反馈信号Fbk之间的相位,并输出两者之间的相位差[12].鉴频鉴相器输出信号Sup和Sdn的符号反映了当前反馈信号“超前”还是“滞后”参考信号,其高电平的长度反映了参考信号与反馈信号之间的相位差大小,因此通过输出信号即可判断相位差的大小和极性.
1.3 时间数字转换器时间数字转换器的功能是以一定的精度对输入的脉冲信号进行量化,将携带时间信息的脉冲信号转换为数字信号,从而实现对时间信息的测量[13],其分辨率决定了环路中参考信号与反馈信号频率的接近程度[14].
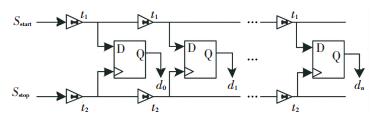
传统的游标尺链型结构见图 2,此结构只能量化当Sstart信号“超前”Sstop信号时的正时间间隔.其基本工作原理如下:Sstart信号和Sstop信号为鉴频鉴相器检测输出的相位差信号,当Sstart信号与Sstop信号分别沿着上下两条延时线传播时,每经过一级延时单元,它们之间的相位差就会减小t1-t2.当Sstart信号滞后Sstop信号时,D触发器的输出为0;当Sstart信号超前Sstop信号时,D触发器的输出为1. d0到dn为输出的温度码,Sstart信号与Sstop信号之间的初始相位差为TIN,温度码中最后一个0出现在第n级,则TDC所量化输出的相位差与初始相位差之间的关系为
| $ n \times ({t_1} - {t_2}) \le {T_{IN}} < \left( {n + 1} \right) \times ({t_1} - {t_2}){\rm{ }}. $ | (1) |
|
图 2 传统的游标尺链型结构 Figure 2 Structure of traditional vernier chain |
由于受各种因素的影响,延时单元可能会有一定的延时偏差,现假设第m级延时单元的延时差偏差值为λm,则第m级延时单元的延时差可修正为
| $ {{T_{{\rm{RES}}, m}} = \left( {{t_1} - {t_2}} \right) + {\lambda _m}, } $ | (2) |
因此,相位差为
| $ {{T_{{\rm{IN}}}} = k \times {T_{{\rm{RES}}, m}} + \sum\limits_{m = 1}^k {} {\lambda _m}, } $ | (3) |
延时单元差值的标准差为
| $ {{\rm{std}}\left( {{T_{{\rm{RES}}, m}}} \right) = {\rm{std}}\left( {{\lambda _m}} \right) = {\rm{std}}\left( \lambda \right), } $ | (4) |
则相位差TIN的不确定度为
| $ {{\rm{std}}\left( {{T_{{\rm{IN}}}}} \right) = {\rm{std}}\left( \lambda \right) \times \sqrt k {\rm{ }}.} $ | (5) |
上式中,std(TIN)代表相位差的不确定度,其与经过的延时线的长度k有关,k越大,则量化单元的相位差不确定度就越大.
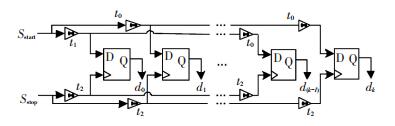
在保证精度、动态范围的前提下,可以采用缩短单延时线长度的方法降低量化相位差的不确定度.因此,本文提出双通道差分延时线型结构见图 3.与传统游标尺链型结构不同的是,其延时线由奇数级的延时单元线和偶数级延时单元线构成,且第一级延时单元的延时差值为其它级的一半,延时线的长度减少为原来的一半,量化相位差的不确定度降低为原来的70.7%.
|
图 3 双通道差分延时线型结构 Figure 3 Structure of double-channel differential delay line |
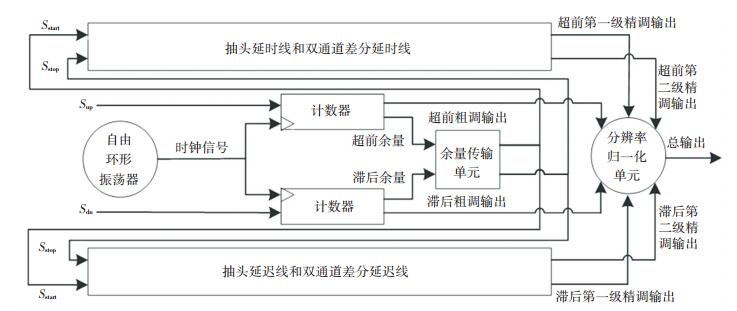
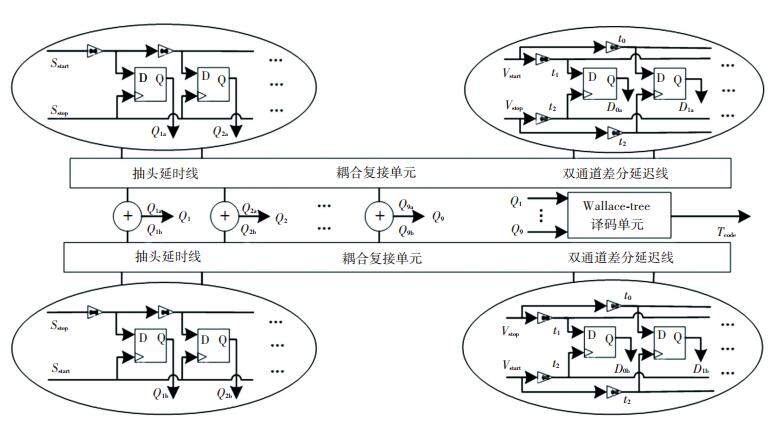
本文提出的三步对称式层次型TDC电路由计数器量化单元、抽头延时线量化单元、双通道差分延时线量化单元、Wallace-tree译码单元、自由环形振荡器(Free Ring Oscillator, FRO)、耦合复接单元、分辨率归一化单元和余量传输单元组成,其结构见图 4. TDC结构的核心电路为:第一级精调抽头延迟线量化单元和第二级精调双通道差分延迟线单元,其结构见图 5.
|
图 4 三步对称式层次型TDC结构 Figure 4 Structure of three-step symmetric hierarchical TDC |
|
图 5 抽头延迟线和双通道差分延迟线结构 Figure 5 Structure of tapped delay line and double-channel differential delay line |
TDC的工作原理:首先由自由环形振荡器提供时钟信号给计数器粗调单元,在相位差信号Sup或Sdn的上升沿到来时,对相位差信号的高电平时间长度进行量化,在相位差信号的下降沿到来时,通过余量传输单元将剩余的相位差信号Sstart和Sstop输入到第一级精调抽头延迟线结构单元中.在Sstart信号的上升沿时,Sstart信号在抽头延时线中开始传播,当耦合复接器中的Sclktime耦合信号检测到Sstart信号为低电平时,记录下此时的时刻,在Sclktime信号的上升沿时,Sstop信号被置为高电平,将采样后获得的5位温度码值Q[1:5]通过Wallace-tree译码单元转换,得到所传过的延时单元级级数.此时耦合复接器将剩余的相位差送入第二级精调双通道差分延迟线单元,Vstop信号对Vstart信号进行采样,在Vstop信号追上Vstart信号之前,对应的温度码值为1,在Vstop追上Vstart信号后,对应的温度码为0.将奇通道和偶通道采样后得到的温度码先按位异或后再按位相加,如果相加后的和为1,则奇通道的4位温度码作为输出温度码Q[6:9],否则将偶通道的4位温度码作为输出温度码,经过译码后输出采样的延时差级数.最后通过分辨率归一化单元对各级量化单元的结果进行分辨率归一化处理,并将超前相位差输出和滞后相位差输出进行累加,输出总的量化结果Tout. TDC中的“超前”相位差输出和“滞后”相位差输出以ns为单位的输出公式分别为
| $ \begin{array}{l} {T_{{\rm{up\_out}}}} = {\rm{ }}\left( {{T_{{\rm{fs\_out}}}} + 1} \right) \times 4 - \left( {{T_{{\rm{sc\_out}}}} + 1} \right) \times 0.8 + \\ {T_{{\rm{th\_out}}}} \times 0.2, {T_{{\rm{dn\_out}}}} = 0, \end{array} $ | (6) |
| $ \begin{array}{l} {T_{{\rm{dn\_out}}}} = {\rm{ }}\left( {{T_{{\rm{fs\_out}}}} + 1} \right) \times 4 - \left( {{T_{{\rm{sc\_out}}}} + 1} \right) \times 0.8 + \\ {T_{{\rm{th\_out}}}} \times 0.2, {T_{{\rm{up\_out}}}} = 0. \end{array} $ | (7) |
DCO的主要功能是产生与所获得的频率控制字相对应的时钟周期脉冲信号[15].为了快速调节反馈信号的相位,缩短环路的锁定时间,在DCO的结构中增加了设计的相调电路. DCO主要由自由环形振荡器、分频计数器、累加器、多路选择器、相调电路和一些与或门组成,其与TDC共用一个FRO电路,以免消耗过多的硬件资源.其工作原理:首先根据频率检测电路输出的频率控制字N0获得相应的分频系数,然后分频计数器对自由环形振荡器输出的高频时钟Fclk信号进行分频,获得与参考信号同频的反馈信号Fbk,然后根据DLF滤波后输出的调节控制字Kcn的数值,相调电路中的状态机对反馈信号低电平时间缩短或延长,而高电平时间保持不变,通过调整对齐相位,快速实现环路锁定.
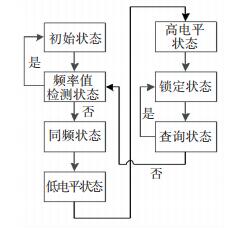
1.5 相调电路在DCO中增设的相调电路是用于相位调节的核心电路.相调电路主要由状态机和下降沿检测电路、D触发器、一些与非门组成.其主要通过状态机来实现不同状态之间的切换,相调电路流程图见图 6,其工作原理:
|
图 6 相调电路流程图 Figure 6 Flow diagram of phase modulation circuit |
最初在初始状态等待由自由环形振荡器和分频计数器产生一个周期的初始频率信号,在初始频率信号的最后高电平输出时刻,进入频率值检测状态检测频率控制字N0是否为零,当N0为零时,回到初始状态继续查询检测N0的大小.否则,进入同频状态实现反馈信号与参考信号同频,开启PFD和TDC量化参考信号和反馈信号的相位差.然后输出与参考信号同频的信号后进入低电平状态,调整反馈信号低电平时间,使反馈信号提前或延迟,再进入高电平状态让反馈信号高电平时间保持不变,实现相位准确对齐后进入锁定状态,在已锁定的反馈信号第一个时钟周期的最后高电平输出时刻进入查询状态,查询频率控制字N0是否发生变化,如果变化,则再次进入同频状态以实现对参考信号的跟踪锁定,否则进入锁定状态正常输出锁定后的反馈信号.
下降沿检测电路会在相调电路中状态机的查询状态时,检测参考信号与反馈信号的下降沿的到来时刻是否一致,如果一致则表明环路已经实现了锁定,此时会将使能信号Epfd和Etdc置为低电平,关闭PFD和TDC电路,避免不必要的电能消耗,从而降低整体电路的功耗.
2 仿真结果与分析根据图 1中所示的全数字锁相环原理框图结构,采用Verilog HDL语言对各部分电路进行自顶向下的RTL级设计,自由环形振荡器FRO由IP核实现.选用Xilinx公司xc7x325t-2ffg900型号FPGA,在ISE2014.2软件中利用XST工具进行综合设计的电路,并且进行仿真,最后在Xpower软件上与传统的基于游标尺链型的全数字锁相环进行功耗测试.下面主要对时间数字转换器和整体电路给出部分仿真结果,对整体电路给出功耗测试结果,然后结合综合后获得的硬件资源消耗量进行功耗分析,最后对电路进行性能对比.
TDC电路的仿真结果见图 7,图中Sup和Sdn信号为待量化的相位差信号,Tfs_out、Tsc_out、Tth_out分别为粗调、第一级精调、第二级精调的输出信号,Tup_out、Tdn_out分别为“超前”相位差输出结果、“滞后”相位差输出结果,Tout为总量化输出结果.在对“超前”相位差信号Sup的第一次量化测试中,量化结果为
| $ \begin{array}{l} {\lambda _{测试1}} = {\rm{ }}\left( {4 + 1} \right) \times 4{\rm{ns}} - \left( {3 + 1} \right) \times 0.8{\rm{ns}} + 2 \times 0.2{\rm{ns}} = \\ 17.2{\rm{ns}} = 1.72 \times {10^4}{\rm{ps}} \approx {\rm{ }}{\lambda _{实际1}} = 17.36{\rm{ns}}. \end{array} $ |

|
图 7 TDC电路仿真结果 Figure 7 Simulation result of TDC circuit |
在对“滞后”相位差信号Sdn的第一次量化测试中,量化结果为
| $ \begin{array}{l} {\lambda _{测试2}} = {\rm{ }}\left( {3 + 1} \right) \times 4{\rm{ns}} - \left( {3 + 1} \right) \times 0.8{\rm{ns}} + 3 \times \\ 0.2{\rm{ns}} = {\rm{ }}13.4{\rm{ns}} = 1.34 \times {10^4}{\rm{ps}} \approx \\ {\lambda _{实际2}} = 13.45{\rm{ns}} \end{array} $ |
在图 7中两次连续对相位差信号的量化过程中,设计的TDC电路都能够有效地量化相位差信号,并将量化误差控制在0.2 ns之内.
图 8为全数字锁相环整体电路的仿真结果,Flock信号为环路的锁定信号.从图中可以看出,在参考信号Fref的第一个到第3个时钟周期内,DCO通过正常分频产生反馈信号Fbk,相调电路对反馈信号的相位进行调节; 在参考信号Fref的第4个时钟周期开始时,环路已经完成锁定,此时Flock置为高电平; 在参考信号Fref的第5个时钟周期开始时,此时Epfd和Etdc置为低电平,关闭PFD和TDC.在参考信号Fref信号第6个时钟周期内,参考信号频率发生了突变,但环路经过一系列调节后,在3个参考时钟周期内再次实现锁定.在图 8中两次连续锁定参考信号的过程中,反馈信号都能够实时监控参考信号的变化,快速完成对参考信号的捕获,达到环路锁定状态.

|
图 8 全数字锁相环整体电路仿真结果 Figure 8 Simulation result of overall ADPLL circuit |
在XST工具上综合后获得的寄存器和查找表消耗量见表 1.使用Xpower软件对整体电路分别在100 MHz、200 MHz、300 MHz和400 MHz频率值上进行测试,得到的功耗值见表 2.由表 1和表 2联合进行对比功耗分析可知,与传统的基于游标尺链型的全数字锁相环相比,虽然硬件资源消耗有所增加,使环路的功耗有所上升,但是采用了下降沿检测电路在环路锁定后适时关闭鉴频鉴相器和时间数字转换器,使整体电路的功耗还是具有一定的降低,整体电路的平均功耗降低约18.1%.
| 表 1 寄存器和查找表消耗量 Table 1 Consumption of register and lookup |
| 表 2 ADPLL的功耗 Table 2 Power consumption of ADPLL mW |
表 3列出了本设计电路与部分已发表文献中的基于TDC的ADPLL性能对比.与文献[8]、[10]、[11]相比,TDC的量化精度分别提高了1.56、1.25、1.2倍; 与文献[8]、[9]相比,ADPLL的锁定速度分别提高了2.5、2.1倍; 由此可见,此全数字锁相环在综合性能方面具有明显的提升.
| 表 3 基于TDC的ADPLL性能对比 Table 3 Comparison of ADPLL performance based on TDC |
针对全数字锁相环常见实现方法中存在的锁定参考信号的时间长、量化精度低、电路功耗大问题,本文设计并实现了一种结合高精度TDC的快速全数字锁相环.提出的TDC使用三步对称式层次型结构,结合抽头延迟线法和双通道差分延迟线法技术,提高了TDC电路的分辨率,将量化相位差信号的误差控制在0.2 ns之内.设计的相调电路使反馈信号能在3个参考信号时钟周期内快速调整相位实现锁定.通过下降沿检测电路在环路锁定后,适时关闭PFD和TDC电路,降低了整体电路的功耗,对比传统的基于游标尺链型的全数字锁相环电路功耗降低了约18.1%.本文设计的全数字锁相环在锁定速度、量化精度、功耗方面具有一定的优势,适用于实时性强、高速、低功耗的现代数字通信系统.
| [1] |
孙高阳, 刘亚静, 李秉格, 等. 一种消除反馈延迟的全数字锁相环[J]. 电工技术学报, 2017, 32(20): 171. SUN Gaoyang, LIU Yajing, LI Bingge, et al. An all-digital phase-locked loop with elimination of feedback delay[J]. Transactions of China Electrotechnical Society, 2017, 32(20): 171. |
| [2] |
黎金英, 艾欣, 邓玉辉. 微电网电压不平衡的分层补偿控制策略[J]. 哈尔滨工业大学学报, 2016, 48(3): 46. LI Jinying, AI Xin, DENG Yuhui. Hierarchical control strategy for voltage unbalance compensation in micro-grid[J]. Journal of Harbin Institute of Technology, 2016, 48(3): 46. DOI:10.3969/j.issn.1009-1971.2016.03.006 |
| [3] |
赵金良, 杨贵杰, 赵品志, 等. 基于SMO的PMSM磁极位置检测技术[J]. 哈尔滨工业大学学报, 2010, 42(1): 95. ZHAO Jinliang, YANG Guijie, ZHAO Pinzhi, et al. Pole position detection techniques of PMSM based on SMO[J]. Journal of Harbin Institute of Technology, 2010, 42(1): 95. DOI:10.3969/j.issn.1009-1971.2010.01.015 |
| [4] |
何峰, 吴乐南. 下一代高效导航卫星信号频谱分析与波形优化[J]. 哈尔滨工业大学学报, 2012, 44(9): 101. HE Feng, WU Lenan. Spectral analysis and waveform optimization of signals for future GNSS[J]. Journal of Harbin Institute of Technology, 2012, 44(9): 101. |
| [5] |
赵品志, 杨贵杰. 基于FPGA的全数字轴角变换算法[J]. 哈尔滨工业大学学报, 2010, 42(12): 1911. ZHAO Pinzhi, YANG Guijie. FPGA-based all-digital resolver-digital conversion algorithm[J]. Journal of Harbin Institute of Technology, 2010, 42(12): 1911. DOI:10.11918/j.issn.0367-6234.2010.12.014 |
| [6] |
马爽, 吴志勇, 高世杰, 等. 改进的大气激光通信PPM调制解调系统设计[J]. 哈尔滨工业大学学报, 2016, 48(5): 105. MA Shuang, WU Zhiyong, GAO Shijie, et al. Design of modified atmospheric laser communication PPM modulation-demodulation system[J]. Journal of Harbin Institute of Technology, 2016, 48(5): 105. |
| [7] |
ELKHOLY A, SAXENA S, NANDWANA R K, et al. A 2.0-5.5 GHz Wide Bandwidth Ring-Based Digital Fractional-N PLL With Extended Range Multi-Modulus Divider[J]. IEEE Journal of Solid-State Circuits, 2016, 51(8): 1771. DOI:10.1109/JSSC.2016.2557807 |
| [8] |
张陆, 张长春, 李卫, 等. 应用于全数字锁相环的时间数字转换器设计[J]. 南京邮电大学学报(自然科学版), 2014, 34(1): 47. ZHANG Lu, ZHANG Changchun, LI Wei, et al. Design of Time-to-Digital Converter for All Digital Phase-locked Loops[J]. Journal of Nanjing University of Posts and Telecommunications, 2014, 34(1): 47. DOI:10.3969/j.issn.1673-5439.2014.01.008 |
| [9] |
ELKHOLY A, ANAND T, CHOI W S, et al. A 3.7mW Low-Noise Wide-Bandwidth 4.5 GHz Digital Fractional-N PLL Using Time Amplifier-Based TDC[J]. IEEE Journal of Solid-State Circuits, 2015, 50(4): 867. DOI:10.1109/JSSC.2014.2385753 |
| [10] |
姚亚峰, 孙金傲, 霍兴华, 等. 一种结合高精度TDC的快速全数字锁相环[J]. 湖南大学学报(自然科学版), 2017, 44(8): 131. YAO Yafeng, SUN Jinao, HUO Xinghua, et al. A fast all digital phase-locked loop combined with high precision TDC[J]. Journal of Hunan University(Natural Science), 2017, 44(8): 131. |
| [11] |
ZENG C, DEEN M J, PENG H. A low-power gateable vernier ring oscillator time-to-digital converter for biomedical imaging applications[J]. IEEE Transactions on Biomedical Circuits & Systems, 2016, 10(2): 445. |
| [12] |
CHOI Y H, KIM B, SIM J Y, et al. A phase-interpolator-based fractional counter for all-digital fractional-N phase-locked loop[J]. IEEE Transactions on Circuits & Systems Ⅱ Express Briefs, 2017, 64(3): 249. |
| [13] |
KIM S, HONG S, CHANGC S, et al. A 2 GHz synthesized fractional-N ADPLL with dual-referenced interpolating TDC[J]. IEEE Journal of Solid-State Circuits, 2016, 51(2): 391. DOI:10.1109/JSSC.2015.2494365 |
| [14] |
LIN J M, YANG C Y. A fast-locking all-digital phase-locked loop with dynamic loop bandwidth adjustment[J]. IEEE Transactions on Circuits & Systems Ⅰ: Regular Papers, 2015, 62(10): 2411. |
| [15] |
CHUNG H, ISHIKURO H, KURODA T. A 10-Bit 80-MS/s decision-select successive approximation TDC in 65 nm CMOS[J]. IEEE Journal of Solid-State Circuits, 2012, 47(5): 1232. DOI:10.1109/JSSC.2012.2184640 |
 2018, Vol. 50
2018, Vol. 50


