用CMOS工艺设计高性能、低成本的直接数字频率合成器DDS一直是一项十分具有挑战性的任务^[1-3].DDS一般分为两个功能单元:相位累加器和相位幅度转换.相位累加器一般包括一个溢出加法器和一个反馈寄存器, 用于累加标准频率控制字, 控制输出信号频率.相位幅度转换完成sine/cosine映射, 即实现输入角度到三角函数值的映射^[4-5].给定任意输入频率控制字, DDS将基于输入的频率控制字输出相应频率的正余弦波形信号.但根据传统相位累加器设计, 输出频率和频率控制字的关系为:f_out=F_tw/2^N·f_clk.其中f_out为输出频率, F_tw为频率控制字, 是一个二进制数.N为相位累加器的数据宽度即位宽.f_clk为系统工作时钟.显然, 传统相位累加器会导致输出频率的分辨率为Δf=1/2^N·f_clk, 即输出频率只能是Δf的整数倍^[6].当需要输出例如Δf~2Δf之间的频率时, 就只能进行四舍五入, 输出频率Δf或频率2Δf中的一个来代替, 而不能进行精准的频率输出.一般通过提高相位累加器位宽来提高频率分辨率或降低误差, 例如把累加器位宽从32比特提高到40比特, 可以提高频率分辨率, 但还是不能完全消除频率误差.相位幅度变换有查表法、泰勒级数展开法以及CORDIC(coordinate rotation digital computer)方法等^[7-9].由于CORDIC算法只需通过移位相加运算不断迭代逼近目标值, 具有精度可调、运算速度快、便于硬件实现等特点, 是相位幅度变换电路设计的主流^[10-12].文献[13-15]提出了CORDIC算法的一种经典实现方法, 将整个迭代运算划分为三个阶段完成, 第一阶段进行4位地址的查找表, 第二阶段进行4次蝶形迭代运算, 最后通过合并迭代运算得出输出结果.这种实现方法在保证精度的前提下, 运算速度和电路资源消耗等都有明显改善, 但是需要7个时钟周期的延时才能得到输出结果, 不太适合高速、实时的信号处理与应用.

本文针对传统相位累加器和相位幅度转换电路存在的不足, 提出了一种可以进行精准频率输出的超低时延DDS电路的新型设计.通过增加一个模数可编程的辅助相位累加器, 可以根据输出频率的需要来设置辅助累加器的输入和模数配置, 从而可以实现不同频率的准确输出, 消除了传统相位累加器存在的最小频率分辨率问题.还针对传统的CORDIC实现方法提出了改进, 设计了一种仅需小容量查找表和简单角度校正的实现方法, 免除了迭代运算.改进后的DDS电路能进行准确的频率输出, 完全消除了输出频率误差, 且在电路规模没有增加和保证16位精度的正余弦波输出前提下, 输出时延从7个时钟周期降低到2个时钟周期.本设计更加适合输出频率精度要求高、实时性强的现代数字信号处理应用场合.

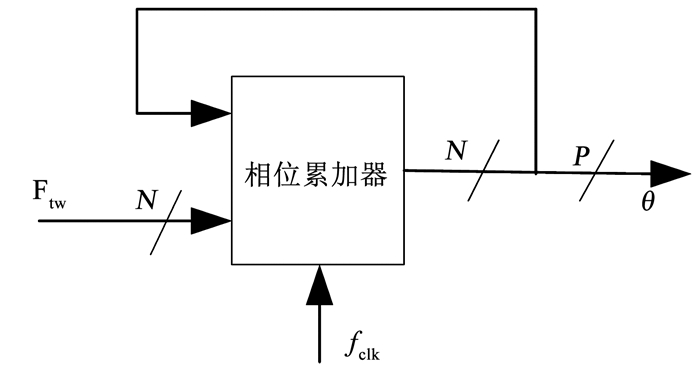
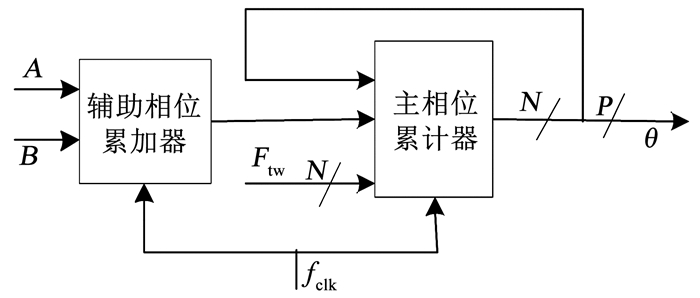
传统相位累加器和改进后的相位累加器分别见图 1和图 2.其中图 1传统相位累加器的输出频率和频率控制字的关系为:f_out=F_tw/2^N·f_clk, 因为这里F_tw必须为整数, 从而存在一个频率分辨率Δf=1/2^N· f_dk的问题.而改进后的图 2相位累加器的输出频率和频率控制字的关系变为:f_out=(F_tw+A/B)/2^N·f_clk, 其中A为辅助相位累加器的频率控制字, B为累加器的模数设置值.通过增加模数可编程的辅助相位累加器设计, 可以通过设置不同的A、B取值, (F_tw+A/B)使可以为任意小数, 从而可以实现精确频率输出, 消除了最小频率分辨率的问题.

Fig. 1

图 1 传统累加器结构 Fig. 1 Traditional accumulator structure

Fig. 2

图 2 模数可编程累加器结构 Fig. 2 Modulo programnable accamulator structure

传统相位累加器主要依赖于累加器采样时钟速率递归求和频率控制字, 这会在累加器的输出端产生一个时间序列的相位累加值, 该数值线性增大, 直至累加器达到最大值2^N-1并翻转.因此, 累加器具有一个固定模数2^N.相位幅度转换器将N位数值映射到单位圆上, 即将0到2^N-1范围内的二进制值线性映射到0到2π范围内的弧度值.这种映射方法使相位幅度转换器非常有效的将N位相位值转换为D位幅度值.转换过程可以表示为三角函数关系:X=sin(2π/2^N · M), 其中M为累加器的输出数值.当然累加器输出通常会被截断至P位, 忽略(N–P)位的低位数值, 以减少相位幅度转换电路的规模和复杂度.

输出频率由相位累加器的平均翻转率决定:f_out/f_clk=F_tw/2^N, F_tw/2^N为小数比例因子, F_tw、N为正整数.根据时间抽样定理可知:F_tw≤2^N-1-1, 因此输出频率f_out限制在{F_tw/2^N·f_clk}的集合, 可以看出DDS累加器的模数(2^N)决定了DDS的频率分辨率和可能输出频率.由于DDS累加器的模数(2^N)必须为整数, 这意味着传统的DDS电路不能输出准确的f_clk/5, f_clk/10, f_clk/100等频率的波形.

如果累加器模数可调, 将能精确输出任意频率.模数可编程累加器是基于传统累加器结构变化而来的.通过增加一个辅助累加器, 使主累加器看起来改变了模数, 但仍然保持相位幅度转换器要求的以2为基数的幂的映射.假定在32位的系统中, 图 2相位累加器的输出方程式变为:

式中:G, H为整数, 并1≤G≤H/2且.在这里模数可编程不要求H为2的指数, 它可以为任选的正整数, 对于32位系统来说, 对H的唯一限制是, 当分数G/H约至最小项时, H必须满足0＜H＜2³².对于输出频率要满足奈奎斯采样定律, 所以对于H的下限要满足H＞2G.式(2)中F_tw+A/B的形式意味着复合频率调谐字, 其中F_tw表示整数部分, A/B代表小数部分.复合频率调谐字不再受整数的限制, 可以实现任意频率的精确输出.

文献[13-15]中提出了一种经典的三段式CORDIC算法, 该算法取范围为[0, π/4]的输入角度, 用二进制表示为: $\theta = \mathop \sum \limits_{{\rm{k}} = 1}^{\rm{N}} {b_{\rm{k}}}{2^{ - {\rm{k}}}} $, 其中b_k∈{0, 1}, 为输入角度二进制表示的bit值.对于[0, π/4]范围外的角度, 可利用三角函数对称性变换获得.通过角度编码, 令r_k=2b_k-1, 则, $ \theta = {\varphi _0} + \mathop \sum \limits_{{\rm{k}} = 2}^{{\rm{N}} + 1} {r_k}{2^{ - k}}, $, φ₀=1/2-(1/2)^N+1为常数, r_k∈{-1, 1}.通过以φ₀为起始坐标旋转, 每次旋转角度依次为2^-2, 2^-3, …, 2^-k弧度, 且旋转方向由θ的二进制表示的位值决定.这样就可以由下式迭代产生输入角的正余弦值.

对tan θ_k进行泰勒展开即可发现, 在k≥N/3时, tan θ_k≈θ_k≈2^-k近似所导致的误差不影响计算精度, 可利用传统CORDIC算法的蝶形迭代计算.在k≥N/2时, tan θ_k≈2^-k, cos θ_k≈1.则式(3)可化简为

因此当k≥N/2时, 利用公式(4)只需要简单的位移和合并就可以得到结果.

经典三段式CORDIC算法的思想主要是把原来需要的N次迭代运算划分为三个阶段来实现:在k＜N/3, 将计算结果存入ROM表作为下一阶段的输入.在N/3≤k＜N/2, 通过传统CORDIC算法的蝶形迭代去计算.在k≥N/2, 通过公式(4)只需要简单的位移和合并相加一步来完成.最后通过三角函数的对称性变换输出整个圆周角度的计算值.

本文提出的基于小容量查找表的超低时延CORDIC算法, 是对三阶段实现CORDIC算法基础上的进一步改进.将限定在[0, π/4]的输入角度值θ用N位二进制表示为: $ \theta = {\varphi _0} + \mathop \sum \limits_{{\rm{k}} = 2}^{{\rm{N}} + 1} {r_{\rm{k}}}{2^{ - {\rm{k}}}}$.并θ将用α和β两部分表示, α表示高6bit角度b₀, b₁, …, b₅的实际值, β表示剩余角度b₆, b₇, …, b_N-2, b_N-1的实际值, 则, θ=α+β因此:

由前可知, 当θ比较小时, sin θ≈θ, cos θ≈1因此可将式(5)化简为:

由于π/4≈2^-1+2^-2+2^-5+2^-8+2^-12, 所以查找表的地址只需从000 000~110 010, 将输入角度值θ前6bit对应的角度值通过式(3)得到迭代计算结果存储到ROM表里.剩余比特的角度值按照式(6)对输入校对进行校正, 即可得到高精度的正余弦值.

对于16bit精度的输出要求, 超低时延CORDIC算法的主要思想是, 第一阶段通过查找表来得到输入角度前6bit角度值的正余弦作为下一阶段的初始值, 查找表具体存储内容如表 1所示; 第二阶段将其他比特的角度值利用式(6)来对查找表的结果进行校正, 得到精准的输入角度对应的正余弦值, 再通过三角对称性转换来得到整个圆周内角度对应的正余弦值.跟三段式实现方法相比, 主要是省去了中间的迭代运算环节, 大大降低了输出时延.

表 1

表 1 ROM查找表 Tab. 1 ROM lookup table Addr x7(cos α) y7(sin α) 000 000 011 111 111 111 111 010 000 000 001 111 111 111 000 001 011 111 111 111 011 010 000 000 101 111 111 111 000 010 011 111 111 110 011 010 000 001 001 111 111 110 000 011 011 111 111 100 111 010 000 001 101 111 111 100 … … … 110 000 010 111 001 111 100 010 01 010 111 111 110 1001 110 001 010 110 111 001 010 110 01 010 111 111 110 1001 110 010 010 110 100 010 110 100 01 011 010 110 101 1011

表 1 ROM查找表 Tab. 1 ROM lookup table

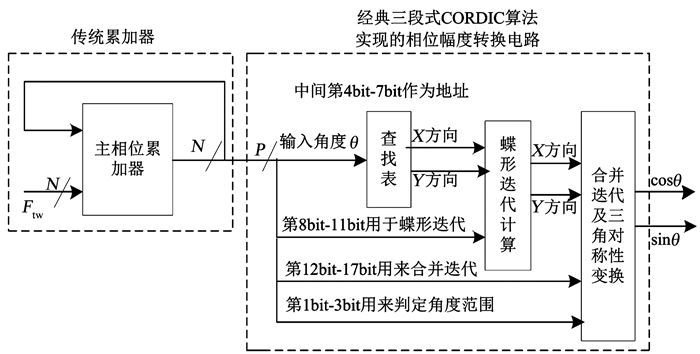
在采用相同指标前提条件下, 对传统DDS和改进后的DDS进行了具体实现.其实现原理框图分别如图 3和图 4所示.相位累加器均取32位位宽, 参考时钟取f_dk=100 MHz, 正余弦波输出信号的位宽取16位(1bit符号位+15bit小数位), 输出频率取1/100·f_clk, 即f_out=1.0 MHz.

Fig. 3

图 3 传统DDS设计原理框图 Fig. 3 Traditional DDS design block diagram

Fig. 4

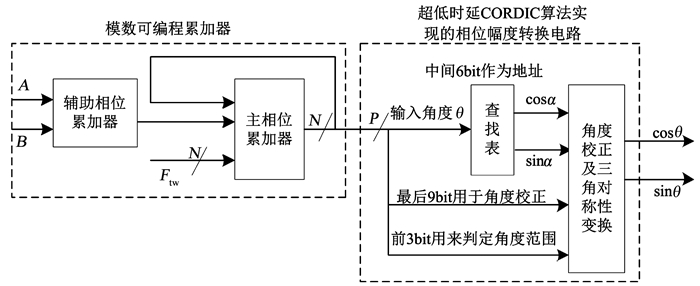
图 4 改进后的DDS输出余弦值误差 Fig. 4 Improved DDS output cosine error

对于传统DDS而言, 要想得到1/100·f_clk, 由f_out/f_clk=F_tw/2³²=1/100, 可得F_tw=42 949 672.96, 而F_tw必须为整数, 取其F_tw=42 949 672, 这时输出频率f_out≈0.999 999 MHz, 其必然存在输出误差.但由于传统累加器的频率控制字必须为整数, 所以它必然不能消除这个输出频率的误差.另外, 其相位幅度变换电路分为3个阶段实现, 电路相对比较复杂, 从输入到输出, 总共需要7个时钟周期的处理时间, 输出延时也偏大.

而对于改进后的DDS而言, 要想得到1/100·f_clk, 即f_out/f_clk=1/100, 由式(1)可知G=1, H=100.再根据式(2)计算可得F_tw=42 949 672, A=24, B=25, 即可精度得到f_out=1.0 MHz的输出频率, 不再存在输出频率误差问题.显然, 改进后的DDS可以通过不同的和A、B设置, 实现任意频率的无误差输出.另外, 改进后的DDS相位幅度变换电路主要由小容量查找表和输出校正电路组成, 从输入到输出, 只需要2个时钟周期的处理时间, 大大降低了输出延时.

将文献[15]的DDS实现方法和本文改进后的DDS用Verilog HDL进行了实现, 并将代码用XILINX公司的xc7k325t-2ffg900型号的FPGA在ISE14.2软件环境下利用XST进行了综合, 其硬件资源消耗、输出延时、最大工作频率等指标如表 2所示, 电路功耗如表 3所示.可见, 改进后的DDS在电路资源消耗方面有所降低, 电路工作频率有所提升, 在输出延时方面有显著改善.

表 2

表 2 综合性能对比表 Tab. 2 Comparison of comprehensive performance 参数 DDS设计方法 文献[15]方法 本文方法 消耗寄存器 346 314 输出延时 7 CLK 2 CLK 最大工作频率 199.440 MHz 242.251 MHz

表 2 综合性能对比表 Tab. 2 Comparison of comprehensive performance

表 3

表 3 电路功耗对比表 Tab. 3 Comparison of circuit power consumption 运行频率/MHz 动态功耗/W 文献[15]方法 本文方法 100 0.107 0.98 150 0.129 0.125 200 0.151 0.148

表 3 电路功耗对比表 Tab. 3 Comparison of circuit power consumption

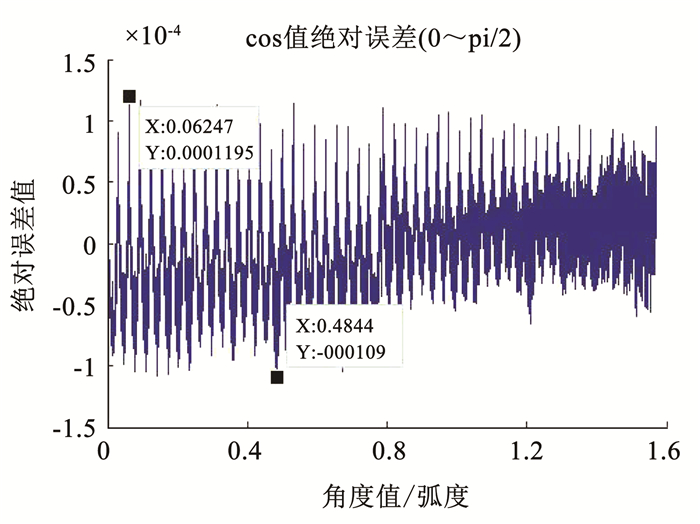
在相同条件设定下, 即相位累加器均取32位位宽, 参考时钟取f_clk=100 MHz, 正余弦波输出信号的位宽取16位(1bit符号位+15bit小数位), 输出频率取1/100·f_clk, 即f_out=1.0 MHz.我们还将电路输出的正余弦值导出来, 与Matlab计算的理论值进行了误差分析和对比.因为三角函数的对称性, 同一种方法输出的正弦值和余弦值误差特性是一致的, 所以这里只给出改进后的DDS电路以及传统DDS电路产生余弦值的绝对误差.它们分别如图 5、图 6所示.由图可得, 改进后的DDS产生余弦值最大绝对误差为8.65×10^-5; 传统DDS余弦值最大绝对误差为11.95×10^-5.改进后的DDS余弦值绝对误差平均值为1.90×10^-5; 传统DDS余弦值绝对误差平均值为2.58×10^-5.可见, 改进DDS在输出精度上也有某种程度的改善.

Fig. 5

图 5 改进后的DDS输出余弦值误差 Fig. 5 Improved DDS output cosine error

Fig. 6

图 6 传统DDS输出余弦值误差 Fig. 6 Traditional DDS output cosine error

本文通过对组成DDS的相位累加器和相位幅度变换电路进行深入分析, 提出了一种能够进行精准频率输出的超低时延DDS电路设计.通过增加一个辅助相位累加器, 使相位累加器的模数可编程, 实现了任意频率的准确输出, 消除了最小频率分辨率问题.还对经典的三段式CORDIC实现方法进行了改进, 完成了一种只需要小容量查找表的CORDIC实现方法, 把输出时延从7个时钟周期降低到2个时钟周期.通过XILINX公司xc7k325t-2ffg900型号FPGA芯片对本设计进行了具体实现, 结果表明, 本文设计的DDS电路在硬件资源消耗、最大工作频率和输出精度上都有所提高, 并且具有输出频率精确、输出时延小、成本低等特点, 更加适合输出频率精度要求高、实时性强的现代数字信号处理应用.