2. 中国铁道科学研究院集团有限公司 铁道建筑研究所,北京 100081
2. Railway Engineering Research Institute, China Academy of Railway Sciences Co. Ltd., Beijing 100081, China
RPC具有优异的力学性能和耐久性能[1],但是受造价偏高等因素影响,尚未得到大规模推广使用.本文研究的RPC-NC叠合梁在充分利用两种混凝土材料性能优势的同时降低了造价,是将RPC材料应用于实际工程中的较为理想的结构形式.
RPC高度的选取不仅决定结构造价,也是影响叠合梁性能的重要因素.Habel等[2]发现UHPFRC可以提高结构的受弯承载力及刚度,延缓裂缝形成,且提高受弯承载力最有效的方式是将受拉筋布置在UHPFRC层中.高丹盈等[3]发现当钢纤维掺加高度从0增加至1/3梁高时,结构抗疲劳性能有明显提升,而从1/3梁高增加至梁高时,对结构疲劳裂缝宽度增长和刚度退化的影响并不显著.李旺旺等[4]发现当裂缝进入失稳扩展阶段后,裂缝宽度增长速率随着RPC高度的增加而降低,RPC可以显著延缓结构裂缝的形成和发展.
相较于普通混凝土,RPC更有利于提高钢筋的拉伸硬化性能[5],二者间良好的黏结性能有利于改善疲劳荷载下结构中的应力分布状态[6].然而如何考虑RPC对裂缝开展起到的延缓作用,以及叠合梁裂缝宽度的计算方法仍需展开进一步研究.
本文通过研究3根部分预应力RPC-NC叠合梁在疲劳荷载作用下的开裂发展特点,理论分析进入疲劳稳定状态后RPC-NC叠合梁最大疲劳裂缝宽度的计算方法,同时对中国现行铁路规范中预应力混凝土梁的最大裂缝宽度计算公式进行修正.
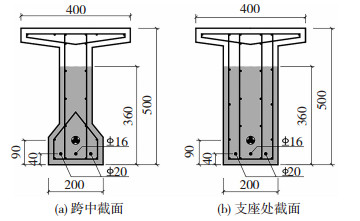
1 试验概况 1.1 模型梁设计与制作模型梁是以中国铁路标准2101号32 m跨度T型梁为原型梁进行缩尺设计得到.模型梁长4.4 m,试验跨度4 m,梁高0.5 m,翼缘宽度0.4 m,腹板厚度0.12 m,模型梁的尺寸及配筋方式完全相同,截面尺寸及配筋情况见图 1.模型梁中RPC高度均为0.36 m,这一高度可以较为充分地发挥下部RPC对叠合梁力学性能的提升作用[4, 7],RPC配合比见表 1.
|
图 1 模型梁截面图(mm) Fig. 1 Cross section of model beams (mm) |
| 表 1 RPC材料配合比 Tab. 1 Mixture ratio of RPC |
制作模型梁时首先绑扎钢筋笼,浇筑下部RPC进行振捣,RPC上表面保持自然粗糙状态,进行72 h温度为75 ℃的高温蒸养.蒸养结束后洒水保持RPC上表面湿润,再浇筑上部C50混凝土,进行7 d的浇水养护,最后进行28 d的自然养护.养护完成后,采用后张法进行张拉,模型梁中的预应力钢绞线采用直线布置,张拉控制应力为1 136 MPa.
| 表 2 混凝土材料基本力学性能 Tab. 2 Mechanical properties of concretes |
| 表 3 钢筋力学性能 Tab. 3 Mechanical properties of rebars |
本研究包括4片模型梁,1片梁进行静载试验,其余3片进行等幅疲劳试验,试验主要参数见表 4.其中梁F1疲劳上、下限荷载的选取基于相似理论,以中-活载为疲劳上限荷载、恒载为疲劳下限荷载为原型,模拟原型梁跨中截面应力状态,在扣除模型梁自重后,得到疲劳下限荷载Pmin=137 kN,疲劳上限荷载Pmax=243 kN,疲劳荷载幅ΔP=106 kN.此外,为进一步探索预应力RPC-NC叠合梁在疲劳损伤发展较为充分状态下的开裂特点,结合试验加载装置性能,分别选取200 kN和300 kN作为梁F2、F3的疲劳荷载幅.
| 表 4 模型梁疲劳试验参数 Tab. 4 Fatigue test parameters of model beams |
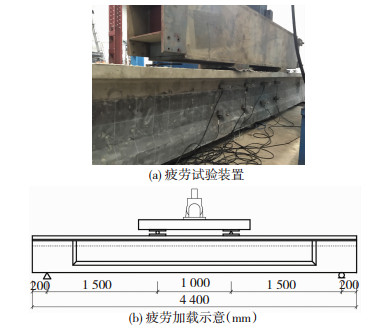
等幅疲劳试验按正弦波加载,加载频率为3 Hz,模型梁采用四点弯曲受力方式,疲劳试验加载情况见图 2.疲劳试验过程中,每循环加载至一定次数时,停机进行一次以疲劳上限荷载为最大值的静力加载试验,通过DJCK-2裂缝观测仪观测并记录模型梁的裂缝发展情况.
|
图 2 疲劳试验加载 Fig. 2 Fatigue test loading |
梁S在静力加载至破坏过程中裂缝发展充分,裂缝分布较密,发生破坏时纯弯段内平均裂缝间距为54.2 mm.梁S的静载裂缝发展示意见图 3,静力加载至243 kN,即梁F1的疲劳上限荷载时未出现裂缝,图中分别标示出加载至梁F2及F3的疲劳上限荷载附近时模型梁的裂缝分布情况.

|
图 3 模型梁静载裂缝发展示意 Fig. 3 Crack patterns of model beam under static load |
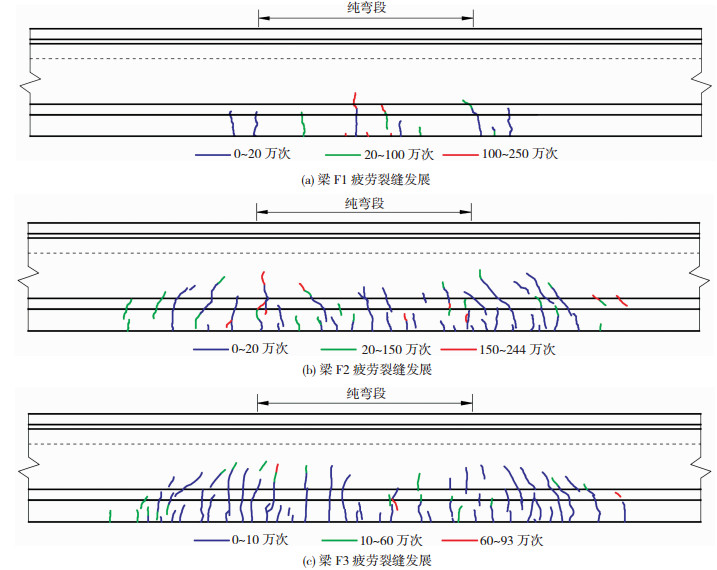
梁F1纯弯段中大部分裂缝在20万次内出现,此后新生成的裂缝较少,尤其是循环次数达到50万次后,主要是已有裂缝向上延伸发展,裂缝宽度无明显增长,新生成裂缝很少且基本不随循环次数的增加而发展,所有裂缝在循环至130万次后基本不再发生变化,模型梁疲劳开裂处于非常稳定的状态.梁F2、F3由于疲劳荷载水平相对较高,纯弯段和剪跨段的裂缝都在初始10~20万次内出现,且大部分裂缝在此后的循环加载中不会继续延伸,即进入了相对稳定的开裂状态,稳定状态下剪跨段内弯剪裂缝的增长相对更为明显.梁F2、F3纯弯段内的主裂缝分别在循环加载超过209万次和84万次后出现了明显的向上延伸和裂缝宽度的增长,其中梁F3在加载至93万次时主裂缝很快向上延伸,裂缝宽度迅速扩展,普通钢筋在纯弯段内疲劳断裂,模型梁发生破坏;梁F2的主裂缝宽度虽在209万次后表现出加速增长的趋势,但加载至244万次时模型梁仍未发生破坏,随后停止疲劳加载.3片模型梁的疲劳裂缝发展示意图见图 4.
|
图 4 模型梁疲劳裂缝发展示意 Fig. 4 Crack patterns of model beams under fatigue loads |
对比图 3、4中模型梁的静载裂缝及疲劳裂缝发展特点可以发现:即使模型梁在静载作用下未发生开裂,随着荷载循环次数的增加,受到钢筋与混凝土间应力重分布和受压区混凝土疲劳性能退化等因素的影响,受拉区混凝土仍有可能发生开裂;相比静载裂缝,疲劳裂缝数量随着循环次数的增长而增加,裂缝长度延伸显著.
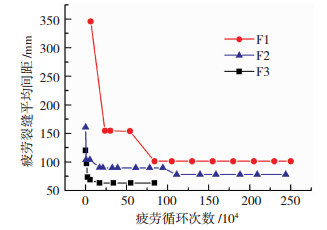
图 5是3片梁在纯弯段内的裂缝平均间距随循环加载次数增长的发展示意图.
|
图 5 平均裂缝间距发展曲线 Fig. 5 Development curves of average crack spacing |
从图 5中可看出,纯弯段内的裂缝平均间距随疲劳循环次数的增长很快进入稳定状态,表现出明显的疲劳2阶段特点.梁F1疲劳荷载水平为0.28Pu,因疲劳荷载水平较低,其第1阶段的疲劳寿命明显大于另外2片梁,进入疲劳稳定阶段后的平均裂缝间距为101.2 mm;梁F2疲劳荷载水平相对较高,为0.39Pu,平均疲劳裂缝间距为78.0 mm;梁F3施加的疲劳荷载水平为0.43Pu,在第93万次发生疲劳破坏,因此梁F3相比其他2片未发生疲劳破坏的梁,裂缝发展得更加充分和均匀,平均裂缝间距相对更小,为63.1 mm,稍大于梁S发生静载破坏时纯弯段内的平均裂缝间距值,模型梁中的箍筋间距为60 mm,与进入稳定阶段后的平均裂缝间距值非常接近.
3 叠合梁疲劳稳定阶段裂缝宽度计算方法在疲劳循环荷载下,RPC-NC叠合梁的裂缝扩展过程呈现出典型的疲劳3阶段特性,进入第3阶段后,梁中纵筋应力迅速增加,裂缝迅速扩展,结构很快发生疲劳破坏.由于疲劳第2阶段占结构总疲劳寿命的90%以上[8],梁结构在正常使用状态下大部分服役时间都处于此阶段,因此该阶段裂缝宽度的发展情况也是设计人员最关心的,影响梁结构的使用状态和耐久性能,本文基于黏结滑移理论,分析推导开裂稳定阶段中叠合梁最大疲劳裂缝宽度的计算方法.
3.1 叠合梁疲劳稳定阶段最大裂缝间距计算从图 4可知,疲劳开裂稳定阶段中叠合梁裂缝间距基本保持不变.根据UHPFRC与钢筋间的黏结应力分布曲线特性[9],可以将其与钢筋间的黏结应力分布图形简化为三角函数表示,由于UHPFRC与RPC性能的高度相似,认为该特性也适用于RPC与钢筋间的黏结性能.由文献[10]得到,黏结应力呈三角函数分布状态下混凝土梁的裂缝间距可表示为
| $ {l_{{\rm{cr}}}} = \frac{{\pi {d_{{\rm{eq}}}}{f_{\rm{t}}}}}{{4{\tau _{\rm{u}}}{\rho _{\rm{e}}}}}, $ | (1) |
式中:ft为裂缝中间截面混凝土受拉应力,当裂缝间距达到最大时,ft等于RPC的抗拉强度fRt;deq为等效钢筋直径;ρe为受拉钢筋有效配筋率,ρe=As/Ac, ef;As和Ac, ef分别为受拉纵筋面积和RPC有效受拉面积;τu为疲劳稳定阶段RPC与钢筋间的黏结强度.
研究发现在未出现明显的疲劳破坏前,钢筋与混凝土间的黏结强度几乎不发生退化[11],即认为开裂稳定阶段时相邻裂缝间钢筋与RPC间的黏结强度与静力黏结强度相同,计算式为[12]
| $ \begin{array}{*{20}{l}} {{\tau _{\rm{u}}} = \left( {2.675 + 0.711\frac{c}{{{d_{{\rm{eq}}}}}}} \right)\left( {0.65 + 1.257\frac{{{d_{{\rm{eq}}}}}}{{{l_{\rm{a}}}}}} \right) \times }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} (0.815 + 0.1{V_{\rm{f}}})\sqrt {{f_{{\rm{cu}}}}} ,} \end{array} $ | (2) |
式中:c为钢筋保护层厚度,la为有效黏结长度,Vf为钢纤维掺量,fcu为RPC立方体抗压强度.
根据式(1)、(2)计算得到叠合梁在疲劳稳定阶段中的最大裂缝间距为117.3 mm.对比试验结果,梁F1最大裂缝间距为191 mm,与计算结果相差较大的原因可能是疲劳荷载水平较低,在疲劳试验有限的加载次数内裂缝尚未发展充分,或是钢筋附近的裂缝还未延伸至梁体表面;梁F2、F3最大裂缝间距分别为108 mm和103 mm,与计算结果较为吻合.
3.2 叠合梁疲劳稳定阶段裂缝宽度计算根据黏结滑移理论可以将叠合梁疲劳最大裂缝宽度表示为
| $ {w_{{\rm{max}}}}(N) = {l_{{\rm{cr,max}}}}[{\bar \varepsilon _{\rm{s}}}(N) - {\bar \varepsilon _{\rm{R}}}(N)], $ | (3) |
式中:lcr, max为最大裂缝间距,εs(N)为N次循环荷载作用下裂缝间钢筋的平均应变,εR(N)为N次循环荷载作用下裂缝间RPC的平均应变.
虽然RPC抗拉应变大于普通混凝土,但仍远小于钢筋应变,为简化计算过程可将式(3)写为
| $ {w_{{\rm{max}}}}(N) = {l_{{\rm{cr,max}}}}{\bar \varepsilon _{\rm{s}}}(N) = {l_{{\rm{cr,max}}}}{\varphi _{\rm{s}}}(N){\bar \varepsilon _{\rm{s}}}(N), $ | (4) |
式中:εs(N)为N次循环荷载作用下裂缝位置处的钢筋应变,φs(N)为钢筋应变不均匀系数[13],φs(N)可表示为
| $ {\varphi _{\rm{s}}}(N) = \frac{{{{\bar \varepsilon }_{\rm{s}}}(N)}}{{{\varepsilon _{\rm{s}}}(N)}} = 1 - \frac{{{f_{{\rm{Rt}}}}{D_{\rm{R}}}(N)(1 + {\rho _{\rm{e}}}n)}}{{2{E_{\rm{s}}}{\rho _{\rm{e}}}\zeta (N){\varepsilon _{\rm{s}}}}}, $ | (5) |
式中:DR(N)为RPC疲劳抗拉强度损伤系数,n为弹模比,εs为静载下裂缝处的钢筋应变,Es为钢筋弹性模量,ζ(N)为钢筋疲劳应变增大系数.
文献[14]中给出RPC疲劳受拉损伤系数可表示为
| $ {D_{\rm{R}}}(N) = 0.01{\rm{ln}}N + 0.428,6 < N \le 250. $ | (6) |
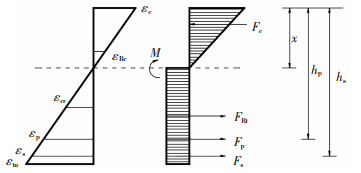
RPC-NC叠合梁开裂截面的简化应力应变分布见图 6.受拉区RPC抗拉强度对截面承载力的贡献通过受拉区均匀分布的等效拉应力αfRt表示,等效系数α的取值参考文献[15].
|
图 6 叠合梁开裂截面应力图 Fig. 6 Stress pattern in cracked section of composite beam |
实际工程中,桥梁结构在绝大部分情况下处于正常使用极限状态,梁结构承受高周低幅疲劳荷载.故本文采用的疲劳荷载水平普遍较低,受压区混凝土始终处于弹性受力阶段,虽然叠合梁中有少部分RPC进入受压区,但是该部分RPC位于中性轴附近,因此为方便计算认为受压区材料均为普通混凝土.
根据截面力矩平衡条件以及平截面假定可以得到:
| $ \frac{{{\varepsilon _{\rm{c}}}}}{x} = \frac{{{\varepsilon _{\rm{s}}}}}{{{h_{\rm{s}}} - x}} = \frac{{{\varepsilon _{\rm{p}}} - {\varepsilon _{{\rm{pe}}}} - {\varepsilon _{{\rm{pc}}}}}}{{{h_{\rm{p}}} - x}}, $ | (7) |
| $ \begin{array}{*{20}{l}} {M = {\varepsilon _{\rm{s}}}{E_{\rm{s}}}{A_{\rm{s}}}({h_{\rm{s}}} - x) + {\varepsilon _{\rm{p}}}{E_{\rm{p}}}{A_{\rm{p}}}({h_{\rm{p}}} - x) + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \alpha {f_{{\rm{Rt}}}}(h - x)[(h + x)/2 - x].} \end{array} $ | (8) |
式中:x为受压区混凝土合力作用点到受压边缘的距离,εc为疲劳荷载作用下压区NC应变,εs为普通钢筋应变,εp为预应力筋应变,εpe为预应力筋的有效预应力对应的应变,εpc为由预应力引起的预应力筋位置处混凝土有效应变.
求解式(7)、(8)即可得到开裂截面位置处的钢筋应变εs.
3.2.2 开裂截面钢筋疲劳应变增大系数计算钢筋在重复荷载作用下疲劳损伤不断累积,钢筋有效承载面积随疲劳损伤的增加而逐渐减小,导致钢筋应变随循环次数的增加逐渐增大,则钢筋应变增大系数表达式为
| $ \zeta (N) = \frac{{{\varepsilon _{\rm{s}}}(N)}}{{{\varepsilon _{\rm{s}}}}} = \frac{{{A_{\rm{s}}}}}{{{A_{\rm{s}}}(N)}} = \frac{1}{{1 - {D_{\rm{s}}}(N)}}, $ | (9) |
式中:As(N)为疲劳循环N次后钢筋有效承载面积,Ds(N)为钢筋疲劳损伤.由连续损伤力学理论可知,不存在初始残余应变的情况下,钢筋疲劳损伤和累积残余应变间的关系为[16]
| $ {D_{\rm{s}}}(N) = \frac{{{\varepsilon _{{\rm{sr}}}}(N)}}{{{\varepsilon _{{\rm{sr}}}}({N_{{\rm{sf}}}})}}[1 - \frac{{{A_{{\rm{sf}}}}}}{{{A_{\rm{s}}}}}], $ | (10) |
式中:Nsf可以通过钢筋的疲劳寿命计算公式得到[17],εsr(N)为疲劳循环N次后钢筋的累积残余应变[18],可表示为
| $ {\varepsilon _{{\rm{sr}}}}(N) = \Delta {\varepsilon _{\rm{s}}}[0.041{\kern 1pt} {\kern 1pt} {\kern 1pt} 5{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{lg}}(N - 1) + 0.057{\kern 1pt} {\kern 1pt} {\kern 1pt} 4], $ | (11) |
式中:Δεs为首次荷载作用下自消压荷载算起的普通钢筋的应变增量.Asf为叠合梁中的普通钢筋达到疲劳临界破坏时的有效承载面积[14],可写为
| $ {A_{{\rm{sf}}}} = (0.24 + 0.76\frac{{{\varepsilon _{\rm{s}}}{E_{\rm{s}}}}}{{{f_{\rm{y}}}}}{\eta _{\rm{s}}}){A_{\rm{s}}}, $ | (12) |
式中:fy为钢筋屈服强度,ηs为考虑2种钢筋黏结性能差异后的应力重分布系数.
综上所述,可以通过式(4)计算得到预应力RPC-NC叠合梁的最大疲劳裂缝宽度.
3.3 规范裂缝宽度计算式的修正中国现行的《铁路桥涵钢筋混凝土和预应力混凝土结构设计规范》[19]中给出部分预应力混凝土梁裂缝最大宽度计算式为
| $ {w_{{\rm{max}}}} = {\alpha _2}{\alpha _3}(2.4{C_{\rm{s}}} + v\frac{d}{{{\mu _{\rm{s}}}}})\frac{{\Delta {\sigma _{{\rm{s2}}}}}}{{{E_{\rm{s}}}}}, $ | (13) |
式中:α2为特征裂缝宽度与平均裂缝宽度相比的扩大系数,α3为考虑运营荷载作用的疲劳增大系数,Cs为纵向钢筋侧面的净保护层厚度,ν为钢筋黏结特性系数,d为钢筋换算直径,μs为纵向受拉钢筋的有效配筋率,Δσs2为消压后按开裂截面计算的非预应力钢筋的应力增量.
根据式(13)计算得到的叠合梁静载裂缝宽度和本文裂缝试验数据进行对比,发现可以对上式引入修正系数β,用以考虑RPC良好的抗拉性能及RPC与钢筋间优异的黏结性能对结构抗裂性能的提升,令其适用于RPC-NC叠合梁的裂缝宽度计算,与试验结果对比发现β取0.36,这一取值和文献[4]中对RPC-NC叠合梁裂缝宽度修正系数的取值非常相近.在此基础上进一步考虑疲劳加载对叠合梁裂缝宽度带来的影响,引入疲劳扩大系数η,根据试验结果拟合得到η的表达式为
| $ \eta = 0.533{\kern 1pt} {\kern 1pt} {\kern 1pt} 5{R^{ - 0.694{\kern 1pt} {\kern 1pt} 3}}{\rm{log}}N. $ | (14) |
则预应力RPC-NC叠合梁最大疲劳裂缝宽度的计算式为
| $ \begin{array}{*{20}{c}} {{w_{{\rm{max}}}} = 0.533{\kern 1pt} {\kern 1pt} {\kern 1pt} 5{R^{ - 0.694{\kern 1pt} {\kern 1pt} 3}}{\alpha _2}{\alpha _3}\beta (2.4{C_{\rm{s}}} + v\frac{d}{{{\rho _{\rm{e}}}}}) \times }\\ {\frac{{\Delta {\sigma _{{\rm{s2}}}}}}{{{E_{\rm{s}}}}}{\rm{log}}N,} \end{array} $ | (15) |
式中R为疲劳荷载应力比,R=Mmin/Mmax.
通过黏结滑移理论计算方法和铁路规范公式两种方法对RPC-NC叠合梁在疲劳稳定阶段中的最大裂缝宽度进行计算,计算结果与试验结果进行对比,见表 5.
| 表 5 最大疲劳裂缝宽度计算值与实测值比较 Tab. 5 Comparison of calculated and measured values of maximum fatigue crack width |
1) RPC-NC叠合梁进入开裂稳定阶段后,平均裂缝间距基本保持不变,且与箍筋间距非常相近.将RPC与钢筋间的黏结应力简化为三角函数分布后,计算得到的最大疲劳裂缝间距与叠合梁在疲劳荷载下裂缝充分发展后的最大裂缝间距值吻合较好.
2) 考虑开裂截面处RPC抗拉性能及疲劳循环加载的影响,基于黏结滑移理论推导得到适用于RPC-NC叠合梁开裂稳定阶段疲劳裂缝宽度的计算方法,能够较为准确地计算RPC-NC叠合梁的最大疲劳裂缝宽度.
3) 为便于设计计算应用,在中国现行铁路规范给出的预应力混凝土梁裂缝宽度计算公式的基础上,考虑了RPC良好的抗拉性能以及RPC与钢筋间优异的黏结性能,通过疲劳扩大系数考虑了循环加载对裂缝宽度的影响.基于铁路规范公式得到的RPC-NC叠合梁的最大疲劳裂缝宽度计算公式形式简单,亦能够较为准确地描述叠合梁疲劳裂缝宽度的发展.
| [1] |
杜任远, 陈宝春. 活性粉末混凝土拱极限承载力试验研究[J]. 工程力学, 2013, 30(5): 42. DU Renyuan, CHEN Baochun. Experimental research on the ultimate load capacity of reactive powder concrete arches[J]. Engineering Mechanics, 2013, 30(5): 42. DOI:10.6052/j.issn.1000-4750.2011.11.0783 |
| [2] |
HABEL K, DENARIÉ E, BRÜHWILER E. Structural response of elements combining Ultrahigh-Performance Fiber-Reinforced Concretes and reinforced concrete[J]. Journal of Structural Engineering, 2006, 132(11): 1793. DOI:10.1061/(ASCE)0733-9445(2006)132:11(1793) |
| [3] |
高丹盈, 张明, 赵军. 疲劳荷载下钢纤维高强混凝土梁裂缝宽度的计算方法[J]. 土木工程学报, 2013, 46(3): 42-43. GAO Danying, ZHANG Ming, ZHAO Jun. Calculating method for crack width of steel fiber reinforced high-strength concrete beams under fatigue loads[J]. China Civil Engineering Journal, 2013, 46(3): 42-43. DOI:10.15951/j.tmgcxb.2013.03.015 |
| [4] |
李旺旺, 季文玉. 预应力RPC-NC结合梁裂缝试验研究[J]. 桥梁建设, 2017, 47(1): 61-63. LI Wangwang, JI Wenyu. Experimental study of cracks in prestressed RPC-NC composite beams[J]. Bridge Construction, 2017, 47(1): 61-63. |
| [5] |
MAKITA T, BRVHWILER E. Tensile fatigue behaviour of Ultra-High Performance Fibre Reinforced Concrete combined with steel rebars (R-UHPFRC)[J]. International Journal of Fatigue, 2014, 59: 151. DOI:10.1016/j.ijfatigue.2013.09.004 |
| [6] |
罗许国, 刘岱鑫. 钢筋活性粉末混凝土梁的疲劳性能试验研究[J]. 西安建筑科技大学学报(自然科学版), 2016, 48(4): 487-488. LUO Xuguo, LIU Daixin. Research on the fatigue performance of reinforced reactive powered concrete beam[J]. Journal of Xi'an University of Architecture & Technology (Natural Science Edition), 2016, 48(4): 487-488. DOI:10.15986/j.1006-7930.2016.08.005 |
| [7] |
季文玉, 李旺旺, 王珏. 预应力RPC-NC叠合梁抗弯延性试验分析[J]. 哈尔滨工业大学学报, 2017, 49(6): 23. JI Wenyu, LI Wangwang, WANG Jue. Experiment alanalysis on flexural ductility of prestressed RPC-NC composite beam[J]. Journal of Harbin Institute of Technology, 2017, 49(6): 23. DOI:10.11918/j.issn.0367-6234.201606036 |
| [8] |
李进洲, 余志武, 宋力. 重载铁路桥梁疲劳变形和裂缝扩展规律研究[J]. 土木工程学报, 2013, 46(9): 76. LI Jinzhou, YU Zhiwu, SONG Li. Study on fatigue deflection and crack propagation laws of heavy-haul railway bridges[J]. China Civil Engineering Journal, 2013, 46(9): 76. DOI:10.15951/j.tmgcxb.2013.09.002 |
| [9] |
LAGIER F, MASSICOTTE B, CHARRON J P. Experimental investigation of bond stress distribution and bond strength in unconfined UHPFRC lap splices under direct tension[J]. Cement and Concrete Composites, 2016, 74: 32. DOI:10.1016/j.cemconcomp.2016.08.004 |
| [10] |
赵国藩, 王清湘. 钢筋混凝土构件裂缝宽度分析的应力图形和计算模式[J]. 大连工学院学报, 1984(4): 90. ZHAO Guofan, WANG Qingxiang. Stress distribution and calculation formula for crack width analysis of reinforced concrete members[J]. Journal of Dalian University of Technology, 1984(4): 90. |
| [11] |
OH B H, KIM S H. Realistic models for local bond stress-slip of reinforced concrete under repeated loading[J]. Journal of Structural Engineering, 2007, 133(2): 223. DOI:10.1061/(ASCE)0733-9445(2007)133:2(216) |
| [12] |
安明喆, 贾方方, 余自若, 等. 活性粉末混凝土受弯构件中钢筋粘结性能[J]. 哈尔滨工业大学学报, 2013, 45(8): 109. AN Mingzhe, JIA Fangfang, YU Ziruo, et al. Bond properties of reinforcement anchored in reactive powder concrete flexural members[J]. Journal of Harbin Institute of Technology, 2013, 45(8): 109. |
| [13] |
白生翔, 李引擎. 受拉钢筋应变不均匀系数与混凝土等效拉应力的关系[J]. 工业建筑, 1985(9): 45. BAI Shengxiang, LI Yinqing. Relationship between the strain unevenness coefficient of tensile reinforcement and the equivalent tensile stress of concrete[J]. Industrial Construction, 1985(9): 45. |
| [14] |
王珏, 季文玉, 李旺旺. 预应力活性粉末混凝土-普通混凝土叠合梁疲劳全过程分析[J]. 浙江大学学报(工学版), 2019, 53(5): 918. WANG Jue, JI Wenyu, LI Wangwang. Full-range analysis on fatigue performance of prestressed reactive powder concrete-normal concrete composite beam[J]. Journal of Zhejiang University (Engineering Science), 2019, 53(5): 918. DOI:10.3785/j.issn.1008-973X.2019.05.012 |
| [15] |
李莉.活性粉末混凝土梁受力性能及设计方法研究[D].哈尔滨: 哈尔滨工业大学, 2010: 81 LI Li. Mechanical behavior and design method for reactive powder concrete beams[D]. Harbin: Harbin Institute of Technology, 2010: 81 |
| [16] |
PETRYNA Y S, PFANNER D, STANGENBERG F, et al. Reliability of reinforced concrete structures under fatigue[J]. Reliability Engineering & System Safety, 2002, 77(3): 255. DOI:10.1016/s0951-8320(02)00058-3 |
| [17] |
曾志斌, 李之榕. 普通混凝土梁用钢筋的疲劳S-N曲线研究[J]. 土木工程学报, 1999(5): 12. ZENG Zhibin, LI Zhirong. Study on S-N curve of steel reinforcement in ordinary reinforced concrete beam[J]. China Civil Engineering Journal, 1999(5): 12. |
| [18] |
钱永久. 疲劳荷载作用下部分预应力混凝土梁的裂缝控制[J]. 西南交通大学学报, 1987(4): 107. QIAN Yongjiu. Control of crack on partially prestressed concrete beam under fatigue load[J]. Journal of Southwest Jiaotong University, 1987(4): 107. |
| [19] |
中华人民共和国铁道部.铁路桥涵钢筋混凝土和预应力混凝土结构设计规范: TB 10002.3—2005[S].北京: 中国铁道出版社, 2010: 63 Ministry of Railways of the People's Republic of China. Code for design on reinforced and prestressed concrete structure of railway bridge and culvert: TB 10002.3—2005[S]. Beijing: China Railway Publishing House, 2010: 63 |
 2020, Vol. 52
2020, Vol. 52



 16
16