2. 核资源与环境国家重点实验室(东华理工大学),南昌 330013
2. State Key Laboratory for Nuclear Resources and Environment(East China University of Technology), Nanchang 330013, China
脆性是指岩石在受力状态下产生微小塑性变形就发生破坏、承载能力急剧丧失的性质.脆性特征评价对于岩石(尤其是深部岩石)力学研究具有非常重要的意义,在岩体工程领域有着广泛的应用.对于深部岩体工程实际来说,岩石处于高地应力环境,岩石脆性程度与岩石可压裂性、开挖损伤程度以及岩爆发生概率的评估和预测密切相关.在高放废物深地质处置及资源开发利用等工程中,岩石脆性指数是硐室围岩稳定和资源开采效率评价的重要指标.
对岩石的脆性评价,国内外诸多学者进行了大量研究,到目前为止已有20多种脆性指标,但仍没有一种被广泛接受的岩石脆性指数计算方法[1].任岩等[2]总结了各种常用的脆性特征评价方法,分析了不同脆性指标的适用性和局限性; Quinn和廖东良等[3-4]提出以所含脆性矿物的硬度和韧性差异来表征岩石脆性; Altindag[5]认为抗压强度和抗拉强度的差异更能反映岩石的脆性程度.与其他方法相比,考虑岩石应力-应变全过程的脆性指标能直观有效地表征岩石的脆性特征. Bishop[6]提出了岩石发生破坏后应力-应变曲线峰后应力降的脆性指标; Hajiabdolmajid等[7-8]考虑曲线峰值应变和残余应变建立脆性指数; 李庆辉等[9]提出了同时考虑曲线峰值前后力学特征的脆性指标; 周辉等[10]建立了考虑岩石屈服破坏过程峰后应力降的相对大小和绝对速率的脆性指标; Aubertin等[11]将脆性指标定义为曲线峰值应力处弹性应变能与峰值处的总能量之比; Tarasov等[12]认为峰后岩石破裂能与峰后可释放弹性能的比值可作为岩石脆性指标; Munoz等[13]采用达峰值应力时的可逆弹性能与全过程所储存总能量之比来定义脆性指数; 夏英杰等[14-15]提出了综合考虑岩石峰后应力降速率与破坏时所释放弹性能和峰前总能量之比的岩石脆性指标,并通过数值模拟分析了力学参数的变化对岩石脆性破坏模式的影响; 李明等[16]通过有限元数值模拟,研究了岩石弹性模量等力学参数对岩石脆性破坏的影响,分析了不同脆性指数的有效性; 宋洪强等[17]通过考虑岩石破坏全过程峰前和峰后阶段的能量演化特征提出了一种基于改进的能量跌落系数的脆性指标.
岩石脆性评价方法种类繁多,现有诸多方法计算的脆性指标普遍存在一定的局限性.然而,岩石脆性评价的重要性又促使研究者探索一种合适的脆性衡量方法.为此,考虑岩石变形破坏全过程,通过引入统计损伤本构模型,较好地模拟岩石应力-应变全过程曲线,分析岩石的损伤演化规律,建立一种基于损伤本构关系的岩石脆性评价新方法,提出的脆性指数计算方法具有良好的适用性和应用价值,能较好地表征岩石的脆性特征.
1 国内外脆性评价方法国内外脆性评价方法如表 1所示,可归纳为6大类:基于强度特征的脆性指标[1, 5](B1~B4)、基于归一化弹性模量和泊松比的脆性指标[18](B5)、基于全应力-应变曲线及能量关系的脆性指标[6-15, 17-18](B6~B14)、基于岩体内摩擦角和破裂角的脆性指标[12](B15、B16)、基于矿物组分的脆性指标[19](B17)以及基于断裂韧性和硬度的脆性指标[3-4](B18~B20).然而,不同研究领域对岩石脆性有不同的理解,对脆性指标的提出大多基于自己特定的研究目的,其适用性有一定的局限,如考虑矿物组分的脆性指标忽略了成岩作用和外部荷载作用等影响因素; 基于归一化弹性模量和泊松比的脆性指标考虑的影响因素过于单一,且需要大量试验样本; 基于强度特征的脆性指标对脆性的表征不敏感,且随围压变化的脆性指标与实际不相符.
| 表 1 国内外常用的脆性指数计算方法汇总 Tab. 1 Summary of common calculation methods for brittleness index |
近年来,基于应力-应变关系曲线及能量关系的评价方法发展较快,诸多脆性指标有一定适用性.然而,有些指标所考虑的影响因素并不充分,如脆性指数B6未考虑峰后应力跌落速率对岩石脆性的影响,B7未考虑峰值强度的影响,且B6、B7皆未对曲线前段的弹、塑性特征做出分析,B8未考虑峰值强度和峰后残余强度的影响; 有些指标考虑较为全面,但均存在特定情况使脆性指数失效,如B9、B10.此外,以上脆性指标均基于理想化曲线,未考虑实际岩石破坏曲线的细节,如曲线的凹凸及突变等情况.基于能量关系的脆性指标也存在诸多问题,其中应力-应变曲线下每一部分面积所代表能量的物理意义目前还存在争议,对于各部分能量的定义也各不相同.
通过以上分析可知,岩石脆性影响因素较多,现有方法计算的脆性指标在某些特定条件下具有较好的适用性,同时也普遍存在一定的局限性.因此,通过引入能较好反映岩石应力-应变全过程曲线的统计损伤本构关系,在分析了岩石的损伤演化规律后,提出了一种基于统计损伤本构关系的岩石脆性评价新方法,克服了现有大多方法考虑不全面和某些特定情况失效的局限性.
2 基于统计损伤本构关系岩石脆性指标的建立 2.1 岩石统计损伤本构关系自从统计损伤理论被引入到岩石变形全过程模拟以来,诸多学者循着这一思路开展了广泛而深入的研究. Krajcinovic等[20-23]以岩石微元强度服从某种随机分布的角度出发,将连续损伤理论和概率统计理论相结合,建立了岩石统计损伤本构模型.其中又多以Weibull分布、正态分布等函数为基础,通过力学分析手段,建立单场或多场耦合条件下的岩石损伤本构模型,描述岩石在不同受力状态下的应力-应变关系.本文以岩石微元强度服从Weibull随机分布为例,根据应变等价性假设,得到反映岩石破坏全过程的本构模型.
将岩石视为由无数细微单元构成,则岩石破坏过程中,其损伤变量D可以定义为已破坏微元数目与总微元数目之比,即
| $ D = \frac{{{N_{\rm{C}}}}}{N}. $ | (1) |
式中:NC为已破坏微元数目,N为构成岩石的微元总数.
假设岩石微元强度的分布规律服从Weibull分布,其强度分布的表达式为
| $ P(F) = \frac{m}{\eta }{\left( {\frac{F}{\eta }} \right)^{m - 1}}\exp \left[ { - {{\left( {\frac{F}{\eta }} \right)}^m}} \right]. $ | (2) |
式中:m、η为Weibull分布参数,F为Weibull分布变量.
岩体的变形破坏是内部损伤不断萌生、扩展直至贯通的连续过程.因此,损伤变量D与微元强度分布关系可以表示为
| $ D = \int_0^\varepsilon P (\varepsilon ){\rm{d}}\varepsilon = 1 - \exp \left[ { - {{\left( {\frac{\varepsilon }{\eta }} \right)}^m}} \right]. $ | (3) |
根据Lemaitre应变等价性原理,即应力作用在受损材料上引起的应变与等效应力作用在无损材料上引起的应变等价,得到岩石损伤本构的基本关系式:
| $ \sigma = {\sigma ^*}(1 - D) = {E^*}\varepsilon (1 - D). $ | (4) |
式中:σ为名义应力,σ*为等效应力,E*为受损材料的弹性模量,ε为材料应变,D为损伤变量.
根据曹文贵等[20-21]的分析推导可以得到基于Weibull分布的岩石统计损伤本构模型及Weibull分布参数的表达式:
| $ {\sigma _1} = 2\mu {\sigma _3} + E{\varepsilon _1}\exp \left[ { - {{\left( {\frac{{{\varepsilon _1} - \frac{{(1 - 2\mu ){\sigma _3}}}{E}}}{\eta }} \right)}^m}} \right], $ | (5) |
| $ \eta = \left[ {{\varepsilon _{\rm{c}}} - \frac{{(1 - 2\mu ){\sigma _3}}}{E}} \right]{\left[ {\frac{{m{\varepsilon _{\rm{c}}}}}{{{\varepsilon _{\rm{c}}} - (1 - 2\mu ){\sigma _3}/E}}} \right]^{\frac{1}{m}}}, $ | (6) |
| $ m = \frac{{{\varepsilon _{\rm{c}}} - (1 - 2\mu ){\sigma _3}/E}}{{{\varepsilon _{\rm{c}}}\ln \left[ {E{\varepsilon _{\rm{c}}}/\left( {{\sigma _{\rm{c}}} - 2\mu {\sigma _3}} \right)} \right]}}. $ | (7) |
对于单轴来说,可视为三轴试验的一种特殊情况,将σ3=0代入到式(5)~(7)可以得到单轴压缩下岩石损伤本构模型.
对损伤变量进行求导,可得到损伤演化率方程:
| $ {\rm{d}}D = \frac{{\partial D}}{{\partial {\varepsilon _1}}}{\rm{d}}{\varepsilon _1} + \frac{{\partial D}}{{\partial {\sigma _3}}}{\rm{d}}{\sigma _3}. $ | (8) |
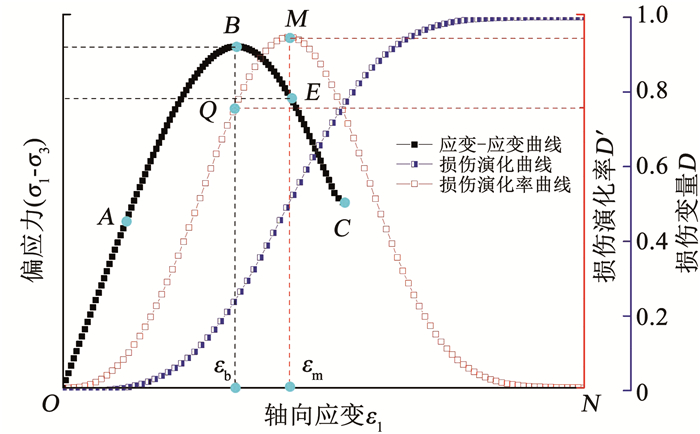
式(5)本构模型所表示岩石应力-应变曲线、式(3)中岩石损伤演化曲线以及式(8)中岩石损伤演化率曲线如图 1所示.
|
图 1 岩石应力-应变及损伤演化曲线 Fig. 1 Stress-strain and damage evolution curve of rock |
分析图 1,结合文献[22-23]的研究可知,岩石统计损伤本构模型可较好地模拟岩石变形破坏全过程,其损伤演化率曲线近似呈正态分布.不同岩石,其三轴压缩条件下应力-应变全过程曲线特征和损伤演化规律不同,脆性演化不同; 对于同种岩石在不同围压下,其破坏特征有着显著差异,损伤演化规律不同,脆性演化亦不同.脆性是岩石变形破坏的重要特性,而应力-应变曲线是岩石不同受力状态下变形破坏的外在表现.因此,以岩石应力-应变全过程曲线和损伤演化规律的差异来建立岩石的脆性指标具有一定的可行性.
2.2 岩石脆性指标BD的建立岩石损伤破坏过程,应力-应变曲线能够直观有效地反映岩石的脆性特征,而统计损伤本构模型能够较好地模拟岩石应力-应变全过程曲线,分析其损伤演化规律.根据这一优势,可以建立反映岩石脆性特征的数学模型.本文在岩石统计损伤本构模型的研究基础上,考虑岩体损伤演化全过程,建立基于统计损伤本构关系的岩石脆性指标:
| $ {B_{\rm{D}}} = \frac{{{D_{{{\max }^\prime }}}}}{{{\varepsilon _{1{\rm{m}}}} \times {{10}^3}}}. $ | (9) |
式中:BD为脆性指数,D′max为最大损伤演化率,ε1m为最大损伤演化率所对应的轴向应变.
损伤演化是根据岩石统计损伤本构模型得到,其能够反映岩石从孔隙压密、弹性变形、裂纹扩展贯通到岩石完全破坏整个过程,即包括应力-应变曲线的峰值前后全过程,过程中考虑了弹性模量E、泊松比μ、峰值强度σc、峰值应变εc、围压σ3,因此,考虑岩石本构关系下的损伤演化全过程来建立岩石脆性评价标准是有意义的.从图 1岩石损伤演化率曲线可知,岩石轴向应力达到峰值B点时,其损伤演化速率为Q点对应的D′值,此时的演化速率并未达到最大值; 损伤演化率达极值M处时,应力-应变曲线处于峰值后的破坏阶段E处; 即损伤演化率曲线OM段包括峰值前、后的岩石损伤破坏过程; 并且损伤演化率曲线近似于正态分布,由于其近乎对称性,仅考虑曲线的一半是可行的.此外,损伤本构模型能够嵌入数值软件进行模拟,分析岩石损伤变形破坏全过程,因此,BD的建立有望为今后岩石脆性的数值模拟研究提供一定的帮助.除上述分析以外,仍需要对BD的合理性和适用性进行验证.
3 脆性指标BD合理性验证 3.1 模型理论论证将不同受力状态下,不同岩石可能出现的应力-应变全过程曲线分为图 2~6中所示的5种对比情况,并根据式(8),得到曲线所对应的岩石损伤演化率,如各图中(b)所示.根据本文提出的脆性指数BD的计算方法式(9)和(b)中损伤演化率曲线可以定量计算不同情况下岩石一和岩石二的脆性程度.

|
图 2 情况1:峰前、峰后曲线一致,峰值应力不同 Fig. 2 Case 1: The curves before and after the peak are consistent, and the peak stresses are different |

|
图 3 情况2:峰值及峰后曲线一致,峰前段不同 Fig. 3 Case 2: The peaks and post-peak curves are consistent, and the pre-peak curves are different |

|
图 4 情况3:峰值及峰前曲线一致,峰后段不同 Fig. 4 Case 3: The peaks and pre-peak curves are consistent, and the post-peak curves are different |

|
图 5 情况4:峰值应变相同,峰前、峰后及峰值应力不同 Fig. 5 Case 4: The peak strains are the same, and the curves before and after the peak and the peak stress are different |

|
图 6 情况5:任意曲线情况 Fig. 6 Case 5: Arbitrary curve situation |
根据图 2,曲线峰前OA段和峰后BC段一致,而岩石一的峰值应力大于岩石二,该情况下岩石一达到破坏时的承载力更大,且破坏时所需要产生的应变大于岩石二.根据式(9)计算可知,岩石一的脆性指数BD大于岩石二,即岩石一的脆性程度大于岩石二,与实际相符; 对于图 3,岩石一与岩石二在曲线峰值B点处应力相同,峰后BC段一致,而峰前OA段不同,岩石一达到峰值时的速率大于岩石二,此时计算的岩石一的脆性指数BD大于岩石二,岩石一的脆性程度大于岩石二,与实际相符; 对于图 4,岩石一与岩石二曲线峰值应力和峰前OA段相同,而峰后BC段不同,岩石一峰后应力的跌落速率大于岩石二,此时计算的脆性指数亦为岩石一大于岩石二,岩石一的脆性程度大于岩石二,也与实际相符.
然而,对于图 5,曲线峰前OA段、峰后BC段及峰值应力皆不相同,达到峰值所对应的峰值应变相同.该情况下,对峰前OA段,岩石二的峰值应力小于岩石一,其达到峰值的速率更大; 对峰后BC段,岩石一的跌落速率更大.因此,从应力-应变线型特征上难以判断出岩石的脆性程度.此时综合脆性指数BD和其他方法计算结果一致,岩石一的脆性指数大于岩石二,即岩石一的脆性程度大于岩石二.对于图 6所示的任意应力应变曲线的对比情况,通过计算可得岩石一的脆性指数BD大于岩石二,岩石一的脆性程度大于岩石二,与实际相符.
通过上述几种不同情况的岩石脆性特征分析可知,基于统计损伤本构关系的脆性指数BD能合理有效地定量反映岩石的脆性程度.
3.2 三轴试验验证——以大理岩[24]和花岗岩[25]三轴试验为例为进一步验证本文提出的脆性评价指标BD的正确性,采用硬脆性岩石大理岩和北山花岗岩三轴压缩试验结果进行验证.
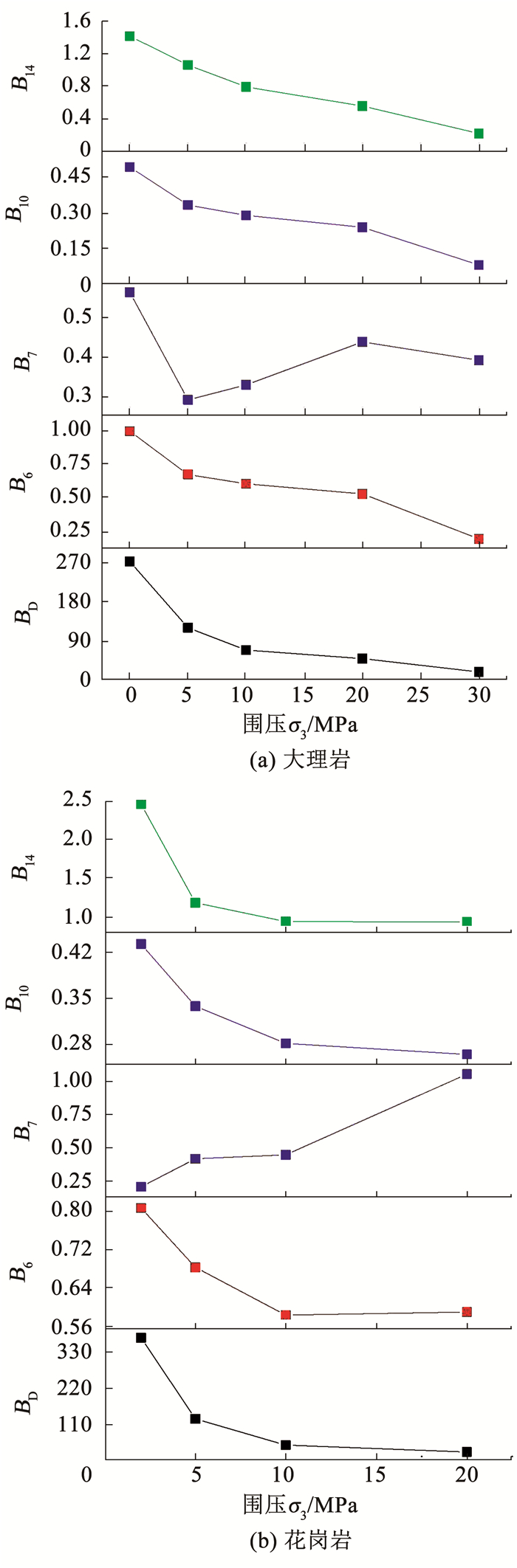
大理岩和花岗岩为典型的硬脆性岩石,杨圣奇等[24]对南阳大理岩的三轴压缩特征进行了分析,陈亮等[25]对北山深部花岗岩受压下的力学行为及损伤特性进行了研究.基于二者的室内三轴压缩试验结果,由于损伤本构模型式(5)~(7)得到的理论曲线不能较好地反映其应力-应变全过程,对其应力-应变曲线在损伤本构关系式(5)下进行拟合,得到了能够较好反映不同围压下应力-应变全过程的拟合曲线及Weibull分布参数的最优值,并将拟合得到的数据代入式(3)和(8),得到损伤演化率曲线,将损伤演化率数据代入到式(9),计算脆性指数BD的值.为直观比较不同脆性指数随围压的变化趋势,同时从表 1中主要选取基于应力-应变曲线的脆性指数进行脆性程度计算,由于B8中峰前可恢复应变不易得到以及B9中标准化系数无法确定,将BD与B6、B7、B10、B14进行对比分析,结果如图 9所示.
|
图 9 不同评价方法下的脆性指数计算值对比 Fig. 9 Comparison of calculated brittleness indexes under different evaluation methods |
文献中物理试验显示的大理岩及花岗岩破裂角均表现出随围压的增大而减小的趋势,岩石的破坏形式由低围压下单剪切面脆性破坏到高围压下多剪切面延性破坏转变.分析图 7~9可知,随围压的增大,岩石的损伤受到抑制,达到的损伤演化速率峰值逐渐减小,脆性程度降低,塑性增强; 对比图 9中两种岩石不同评价方法计算的脆性指数可知,本文提出的脆性指数BD与B6、B10、B14的趋势具有较高的一致性,其表征的岩石脆性程度与三轴试验岩样破坏时破裂角及破裂面特征反映的岩石脆性程度一致,能较好地反映大理岩及花岗岩的脆性特征.

|
图 7 不同围压下大理岩和花岗岩应力-应变及拟合曲线 Fig. 7 Stress-strain curves and fitting curves of marble and granite under different confining pressures |

|
图 8 大理岩和花岗岩损伤演化率曲线 Fig. 8 Damage evolution rate curves of marble and granite |
结合模型理论论证及硬脆性岩石大理岩和北山花岗岩室内三轴压缩试验验证,对比BD所反映的脆性程度可知,基于本构模型损伤演化的脆性评价指标BD能很好衡量岩石的脆性程度,反映岩石脆-塑性转变特征.
4 基于塔木素黏土岩室内试验的脆性评价实例分析深部岩体工程中,岩石的脆性评价具有重大的意义.对于高放废物处置库来说,其处置巷道一般建设在地下深500 m以下,处置库围岩处于一种复杂的中、高地应力环境,岩石的脆性影响开挖掘进效率、开挖过程中开挖损伤程度及开挖损伤区EDZ的范围.塔木素黏土岩是中国高放废物处置库的预选围岩,从现场及室内试验得出,塔木素深部黏土岩含水率和孔隙度低,其含水率在2.5%~5%,孔隙度在8%~12%,为致密岩类,其力学强度、脆性程度要大于一般的泥岩.因此,脆、塑性特征评价对塔木素地区黏土岩高放废物处置库的设计开挖具有深远的意义.
4.1 黏土岩三轴压缩试验本文通过室内三轴压缩试验,得到了塔木素黏土岩的强度参数及应力-应变曲线,为后期工作提供了依据.试验采用ϕ50×100 mm的圆柱形标准试样,所用黏土岩样取自高放废物处置库黏土岩预选区内蒙古塔木素500 m深处,使用TAW-2000微机控制岩石三轴试验机按测试标准对塔木素黏土岩的力学强度进行三轴压缩试验研究,试验中采用轴向位移控制加载,加载速率控制为0.005 mm/min,试样及试样破坏状态如图 10所示,试验结果如表 2所示,应力-应变曲线见图 11.

|
图 10 塔木素黏土岩标准试样及三轴压缩试验破坏状态图 Fig. 10 Standard samples of Tamusu clay rock and failure state images under triaxial compression test |
| 表 2 塔木素黏土岩三轴压缩试验结果及脆性指数计算值 Tab. 2 Results of triaxial compression test of Tamusu clay rock and calculated brittleness indexes |

|
图 11 不同围压下塔木素黏土岩应力-应变曲线 Fig. 11 Stress-strain curves of Tamusu clay rock under different confining pressures |
试验结果表明,随着围压的增大,塔木素黏土岩的抗压强度随之增大,单轴抗压强度约为33.70 MPa.由图 11,12可以看出,由于塔木素黏土岩属致密岩类,其压密阶段不明显,表现出明显的弹性阶段、塑性屈服阶段及破坏阶段.随着围压的增大,黏土岩受到的侧限越大,曲线弹性阶段斜率及达到的峰值随之增大,即变形模量和弹性极限不断增大,而泊松比的变化不明显.对图 10中(b)和(c)所示的黏土岩破坏后的破裂角进行测量,由于高围压15 MPa时的岩样破坏面不明显,不易直接测量破裂角,可采用CT扫描的手段,获得其破坏后微观破裂面发育情况.由物理试验可知,黏土岩破裂面与加载轴线的夹角α从8°增加到44°,即破裂角从单轴时的82°转变到高围压15 MPa时的46°,岩样从劈裂破坏向剪切破坏过度.

|
图 12 塔木素黏土岩损伤变量曲线 Fig. 12 Damage variable curves of Tamusu clay rock |
为了对塔木素黏土岩的脆性特征进行评价,采用提出的基于统计损伤本构关系的脆性指标BD对不同围压下的黏土岩进行定量分析.同时计算脆性指数B6、B7、B10、B14的值,并将脆性指数表征的脆性程度与物理试验中破裂角反映的脆性特征进行对比分析.
对图 11中应力-应变曲线在损伤本构函数式(5)下进行拟合,得到了能够较好反映不同围压下黏土岩应力-应变全过程的拟合曲线及Weibull分布参数的最优值,并将拟合得到的数据代入式(3)和(8),绘制的损伤演化规律曲线见图 12, 13,将损伤演化率数据代入式(9),计算脆性指数BD值.根据表 1计算方法,得到B6、B7、B10、B14以及破裂角的计算结果如表 2所示,并绘制成图 14进行对比.

|
图 13 塔木素黏土岩损伤演化率曲线 Fig. 13 Damage evolution rate curves of Tamusu clay rock |

|
图 14 黏土岩脆性指数BD和B6、B7、B10、B14及破裂角随围压σ3的变化 Fig. 14 Variation of brittleness indexes BD, B6, B7, B10, B14, and rupture angle of clay rock with σ3 |
由图 11~13可以看出,三轴压缩条件下,黏土岩受荷初期主要处于线弹性阶段,真正意义上的线弹性变形不会对岩石产生损伤.因此,该阶段的损伤演化缓慢,演化速率较低.随着轴向应力的增大,裂纹开始萌生和扩展,此时的损伤演化速率逐渐变大.当裂纹贯通、岩石开始破坏时,损伤演化曲线斜率最大,演化速率达到最大值,这一过程损伤最为明显.此后直至岩石完全破坏,过程中岩石损伤演化速率减缓,最终损伤变量趋于1.
随着围压的增大,塔木素黏土岩的损伤速率变小,破坏全过程中损伤速率达到最大值时的轴向应变增大,说明围压的存在抑制了黏土岩损伤的发展,围压越大,黏土岩脆性特征减弱,塑性特征增强.从不同围压下岩样破坏状态中反映出的破裂角差异能够看出,黏土岩在低围压下脆性程度明显,而高围压下塑性程度明显.对比图 14可知,B6、B10、B14能较好地反映黏土岩的脆性特征随围压的变化情况,而B7反映的脆性程度与实际相反.将BD、B6、B7、B10、B14与破裂角所反映的黏土岩脆性程度趋势进行对比可知,与其他脆性指数相比,BD与物理实验结果更为吻合.从图 14可知,随着围压逐渐增大,BD值逐渐减小,黏土岩的脆性降低,塑性特征增强.本文提出的数学模型计算的脆性指数BD值与试验结果有较高的吻合程度.对BD的计算值进行拟合(如图 15所示),可以得到塔木素深部黏土岩脆性指数与围压的关系:

|
图 15 脆性指数BD的计算值及拟合曲线 Fig. 15 Calculated values of BD and the fitting curve |
| $ {B_{\rm{D}}} = 0.11\sigma _3^2 - 5.08{\sigma _3} + 60.44. $ | (10) |
式(10)可以在一定程度上反映在不同围压下塔木素黏土围岩的脆、塑性特征.
5 结论1) 本文建立的脆性指数能有效合理地表征岩石的脆性特征,能基于不同强度准则下、不同随机分布函数下的统计损伤本构模型,分析岩石的损伤演化规律,计算脆性指数,脆性指标BD的适用性具有一定的广度.
2) 随着围压的增大,塔木素地区黏土岩的损伤速率减小,破坏全过程中损伤速率达到最大值时的轴向应变增大,脆性指数BD值减小,即围压的存在抑制了黏土岩损伤的发展,围压越大,黏土岩脆性程度减弱,塑性增强.
3) 脆性指数BD能够定量表征黏土岩的脆性程度,与其他脆性指数相比,BD与物理试验结果吻合度更高.BD=0.11σ32-5.08σ3+60.44可以在一定程度上反映塔木素黏土岩的脆性特征.
| [1] |
ALTINDAG R. Assessment of some brittleness indexes in rock-drilling efficiency[J]. Rock Mechanics and Rock Engineering, 2010, 43(3): 361. DOI:10.1007/s00603-009-0057-x |
| [2] |
任岩, 曹宏, 姚逢昌, 等. 岩石脆性评价方法进展[J]. 石油地球物理勘探, 2018, 53(4): 875. REN Yan, CAO Hong, YAO Fengchang, et al. Review of rock brittleness evaluation methods[J]. Oil Geophysical Prospecting, 2018, 53(4): 875. DOI:10.13810/j.cnki.issn.1000-7210.2018.04.026 |
| [3] |
QUINN J B, QUINN G D. Indentation brittleness of ceramics: A fresh approach[J]. Journal of Materials Science, 1997, 32(16): 4331. DOI:10.1023/A:1018671823059 |
| [4] |
廖东良, 肖立志, 张元春. 基于矿物组分与断裂韧度的页岩地层脆性指数评价模型[J]. 石油钻探技术, 2014, 42(4): 37. LIAO Dongliang, XIAO Lizhi, ZHANG Yuanchun. Evaluation model for shale brittleness index based on mineral content and fracture toughness[J]. Petroleum Drilling Techniques, 2014, 42(4): 37. DOI:10.3969/j.issn.1001-0890.2014.04.007 |
| [5] |
ALTINDAG R. Correlation of specific energy with rock brittleness concepts on rock cutting[J]. Journal of the Southern African Institute of Mining and Metallurgy, 2003, 103(3): 163. |
| [6] |
BISHOP A W. Progressive failure with special reference to the mechanism causing it[C]//Proceedings of the Geotechnical Conference. Olso: [s.n.], 1967: 142
|
| [7] |
HAJIABDOLMAJID V, KAISER P K, MARTIN C D. Modelling brittle failure of rock[J]. International Journal of Rock Mechanics and Mining Sciences, 2002, 39(6): 731. DOI:10.1016/S1365-1609(02)00051-5 |
| [8] |
HAJIABDOLMAJID V, KAISER P. Brittleness of rock and stability assessment in hard rock tunneling[J]. Tunnelling and Underground Space Technology, 2003, 18(1): 35. DOI:10.1016/S0886-7798(02)00100-1 |
| [9] |
李庆辉, 陈勉, 金衍, 等. 页岩脆性的室内评价方法及改进[J]. 岩石力学与工程学报, 2012, 31(8): 1680. LI Qinghui, CHEN Mian, JIN Yan, et al. Indoor evaluation method for shale brittleness and improvement[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(8): 1680. |
| [10] |
周辉, 孟凡震, 张传庆, 等. 基于应力-应变曲线的岩石脆性特征定量评价方法[J]. 岩石力学与工程学报, 2014, 33(6): 1114. ZHOU Hui, MENG Fanzhen, ZHANG Chuanqing, et al. Quantitative evaluation of rock brittleness based on stress-strain curve[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(6): 1114. DOI:10.13722/j.cnki.jrme.2014.06.004 |
| [11] |
AUBERTIN M, GILL D E, SIMON R. On the use of the brittleness index modified (BIM) to estimate the post-peak behavior of rocks[C]//Proceedings of 1st North American Rock Mechanics Symposium. Austin, Texas: American Rock Mechanics Association, 1994: 945
|
| [12] |
TARASOV B, POTVIN Y. Universal criteria for rock brittleness estimation under triaxial compression[J]. International Journal of Rock Mechanics and Mining Sciences, 2013, 59: 57. DOI:10.1016/j.ijrmms.2012.12.011 |
| [13] |
MUNOZ H, TAHERI A, CHANDA E K. Rock drilling performance evaluation by an energy dissipation based rock brittleness index[J]. Rock Mechanics and Rock Engineering, 2016, 49(8): 3343. DOI:10.1007/s00603-016-0986-0 |
| [14] |
夏英杰, 李连崇, 唐春安, 等. 基于峰后应力跌落速率及能量比的岩体脆性特征评价方法[J]. 岩石力学与工程学报, 2016, 35(6): 1141. XIA Yingjie, LI Lianchong, TANG Chun'an, et al. Rock brittleness evaluation based on stress dropping rate after peak stress and energy ratio[J]. Chinese Journal of Rock Mechanics and Engineering, 2016, 35(6): 1141. DOI:10.13722/j.cnki.jrme.2015.0803 |
| [15] |
夏英杰, 李连崇, 唐春安, 等. 储层砂岩破坏特征与脆性指数相关性影响的试验及数值研究[J]. 岩石力学与工程学报, 2017, 36(1): 10. XIA Yingjie, LI Lianchong, TANG Chun'an, et al. Experiment and numerical research on failure characteristic and brittleness index for reservoir sandstone[J]. Chinese Journal of Rock Mechanics and Engineering, 2017, 36(1): 10. DOI:10.13722/j.cnki.jrme.2015.1407 |
| [16] |
李明, 马收, 夏英杰, 等. 基于模拟的岩芯脆性室内评价方法对比与分析[J]. 辽宁工程技术大学学报(自然科学版), 2016, 35(8): 859. LI Ming, MA Shou, XIA Yingjie, et al. Analysis and contrast of indoor brittleness evaluation methods for rock mass based on the simulation[J]. Journal of Liaoning Technical University (Natural Science), 2016, 35(8): 859. DOI:10.11956/j.issn.1008-0562.2016.08.014 |
| [17] |
宋洪强, 左建平, 陈岩, 等. 基于岩石破坏全过程能量特征改进的能量跌落系数[J]. 岩土力学, 2019, 40(1): 91. SONG Hongqiang, ZUO Jianping, CHEN Yan, et al. Revised energy drop coefficient based on energy characteristics in whole process of rock failure[J]. Rock and Soil Mechanics, 2019, 40(1): 91. DOI:10.16285/j.rsm.2017.2275 |
| [18] |
张英, 郭奇峰, 蔡美峰, 等. 硬岩脆性指标与弹性应变能关系初探[J]. 哈尔滨工业大学学报, 2019, 51(6): 79. ZHANG Ying, GUO Qifeng, CAI Meifeng, et al. Preliminary study on relationship between brittleness index and elastic strain energy for hard rock[J]. Journal of Harbin Institute of Technology, 2019, 51(6): 79. DOI:10.11918/j.issn.0367-6234.201809127 |
| [19] |
RICKMAN R, MULLEN M J, PETRE J E, et al. A practical use of shale petrophysics for stimulation design optimization: All shale plays are not clones of the Barnett Shale[R]. Colorado, USA: Society of Petroleum Engineers, 2008
|
| [20] |
KRAJCINOVIC D, SILVA M A G. Statistical aspects of the continuous damage theory[J]. International Journal of Solids and Structures, 1982, 18(7): 551. DOI:10.1016/0020-7683(82)90039-7 |
| [21] |
唐春安. 岩石破裂过程中的灾变[M]. 北京: 煤炭工业出版社, 1993: 10. TANG Chun'an. Catastrophe in rock unstable failure[M]. Beijing: China Coal Industry Publishing House, 1993: 10. |
| [22] |
曹文贵, 方祖烈, 唐学军. 岩石损伤软化统计本构模型之研究[J]. 岩石力学与工程学报, 1998, 17(6): 628. CAO Wengui, FANG Zulie, TANG Xuejun. A study of statistical constitutive model for soft and damaged rocks[J]. Chinese Journal of Rock Mechanics and Engineering, 1998, 17(6): 628. |
| [23] |
徐卫亚, 韦立德. 岩石损伤统计本构模型的研究[J]. 岩石力学与工程学报, 2002, 21(6): 787. XU Weiya, WEI Lide. Study on statistical damage constitutive model of rock[J]. Chinese Journal of Rock Mechanics and Engineering, 2002, 21(6): 787. |
| [24] |
杨圣奇, 徐卫亚, 苏承东. 大理岩三轴压缩变形破坏与能量特征研究[J]. 工程力学, 2007(1): 136. YANG Shengqi, XU Weiya, SU Chengdong. Study on the deformation failure and energy properties of marble specimen under triaxial compression[J]. Engineering Mechanics, 2007(1): 136. |
| [25] |
陈亮, 刘建锋, 王春萍, 等. 北山深部花岗岩弹塑性损伤模型研究[J]. 岩石力学与工程学报, 2013, 32(2): 289. CHEN Liang, LIU Jianfeng, WANG Chunping, et al. Elastoplastic damage model of Beishan deep granite[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(2): 289. |
 2020, Vol. 52
2020, Vol. 52


