双离合自动变速器车辆换挡品质的传统定义是从车辆的平顺性方面来衡量的,即希望车辆能够平顺且无冲击地完成换挡过程[1],研究表明,换挡过程控制的优劣会直接影响整车动力性、舒适性、传动系统耐久性以及燃油经济性[2-6],因此对换挡品质的准确评价具有重要的意义.
目前,主要运用主观评估的方法对换挡品质进行评价,一般是利用有经验驾驶员的感官对换挡品质进行评价.由于主观评价有离散性大、难以量化、稳定性差等问题[7],已经有很多专家对换挡品质评价进行了深入研究.孙贤安等[8]从动力性、经济性、舒适性、传动系统耐久性4个维度提出换挡品质评价指标,基于径向基函数神经网络方法建立了舒适性主客观之间的联系.宋世欣等[9]、王尔烈等[10]、Min等[11]、Park等[12]在控制策略以及优化指标上对双离合自动变速器车辆换挡品质进行提升. Shin等[13]应用了一种基于神经网络的汽车换挡控制器监控器,对换挡的平稳性与精确性进行监控评估.但是,上述研究在指标体系的建立以及评价方法的选择上没有做到主客观综合考虑,一方面无法排除主观的不稳定性以及忽略客观数据对换挡品质的真实反映,另一方面又会完全局限于数据之中而没有发挥主观经验的指导作用,因此都有一定的缺陷.
针对以上问题,本文从3个不同维度提出10个与换挡品质相关的指标,并运用层次聚类方法与专家经验相结合的方式,建立换挡品质评价指标体系.研究了主观权重和客观权重的计算方法,并基于分配最优原则,确定主客观权重的分配比例;构建了基于数据差异性和模糊阈值的隶属度函数,建立模糊综合评价模型,对换挡品质进行评价分析.
1 换挡品质评价体系建立 1.1 多维换挡品质评价指标DCT车辆换挡过程中,换挡时间长短、发动机转速控制等对换挡品质的动力性有较大的影响[14],同时车辆产生的纵向加速度、车速等响应对换挡品质的平顺性也有很好的体现[15].因此选择从时间、发动机转速与纵向加速度3个维度确定换挡品质评价指标.从时间维度选取了换挡时间与换挡延迟时间指标.从发动机转速维度选取了转速梯度、离合器分离转速超调和离合器接合转速超调指标;从汽车纵向加速度维度选取了离合器接合加速度幅值、加速度扰动、正向冲击、负向冲击和加速度振荡指标.上述3个维度提取的多维换挡品质评价指标介绍及其物理意义如表 1所示.
| 表 1 多维换挡品质评价指标 Tab. 1 Multi-dimensional shift quality evaluation index |
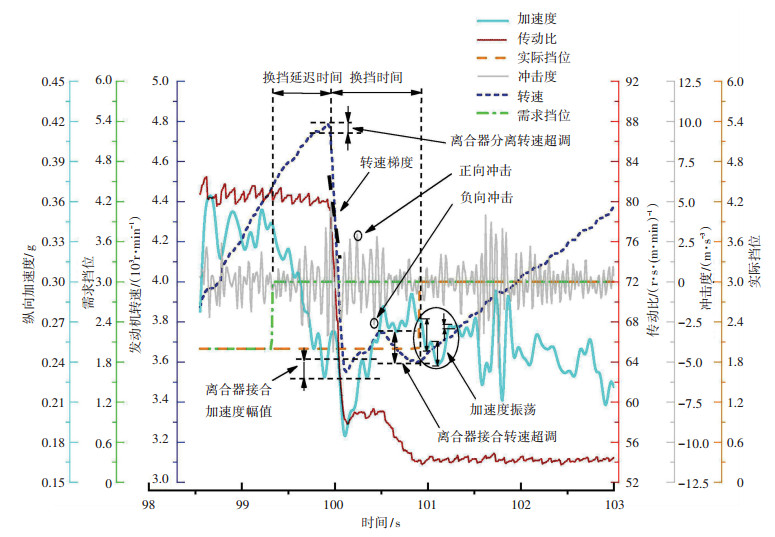
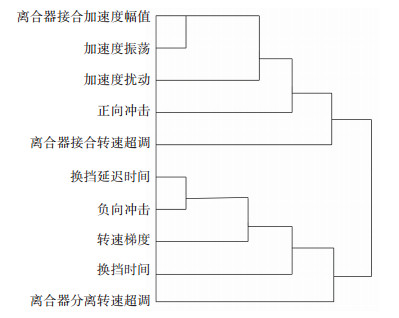
传统换挡过程定义表明, 平顺性是评价换挡过程的一个重要因素[1],有研究提出,动力性是影响换挡品质的另一个重要组成部分[16];因此提出从平顺性与动力性两个角度对换挡品质进行评价.以某一换挡工况试验数据为例,其动态曲线与各指标分布如图 1所示.影响换挡品质的10个评价指标潜在关系以及如何反应换挡品质是未知的.聚类分析是挖掘事物之间潜在联系的常用方法,其中层次聚类在使用中不需要指定类别数目,灵活性大,通过计算各指标类之间的距离进行聚类判断,因此被用来挖掘评价指标与换挡品质之间的映射关系.通过SPSS软件运用该方法对实验获取的多组换挡工况数据进行指标聚类,构建的谱系图如图 2所示.谱系图显示迭代到8次时,评价指标聚为两类,对迭代结果进行分析发现:第1类指标多以时间为主要因素特征,能反映换挡的动力性,第2类指标多由纵向加速度衍生出来的,反映换挡的平顺性.结合专家经验对聚类结果进行验证和调整,例如其中正向冲击指标是速比从开始变化的时刻到速比保持稳定的时刻之间最大正向冲击度值,体现驾驶员后仰的最大程度,反映了换挡过程中的平顺性感受;负向冲击是换挡过程中最大负向冲击度值,反映了DCT换挡过程中动力的丢失情况,因此与换挡过程的动力性关联性较强,与聚类的结果一致;但经主观评估专家验证,离合器分离转速超调产生的效果主观表现为冲击,与换挡的平顺性关联性更大,需调整为平顺性指标.
|
图 1 换挡品质指标分布 Fig. 1 Distribution of shift quality indexes |
|
图 2 换挡品质评价指标聚类谱系图 Fig. 2 Clustering pedigree of shift quality evaluation indexes |
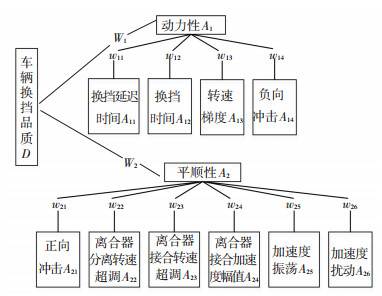
最终建立换挡品质评价体系如图 3所示,其中D为目标层, Ak为一级评价指标, Wk为一级指标权重, Akj为二级评价指标, wkj为二级指标权重.
|
图 3 换挡品质评价体系 Fig. 3 Shift quality evaluation system |
换挡品质评价是一个多层次、多指标的客观评价系统,指标权重的确定是目前适用的评价方法中的关键.换挡品质是人与车的综合反映,一方面与人的感受息息相关,另一方面又是车辆换挡过程信息的真实反映; 因此换挡品质评价应同时考虑受人认知影响的主观权重和受车辆真实反应影响的客观权重,才能对换挡品质进行准确有效地评价.
2.1.1 主观权重层次分析法可以将问题中的变量划分为有序的层次,借鉴专家知识和经验对指标进行重要度比较,能进行定性、定量计算,是常用的主观权重确定方法.在层次分析法中,判断矩阵A建立的准确与否至关重要,专家对重要度进行比较时容易受权威等其他因素的影响,本研究将德尔菲法与层次分析法相结合用于判断矩阵的建立,通过匿名函询的方式对专家们进行采访,要求专家们对换挡品质评价指标重要性程度通过常用的1-9尺度来判断[17],对V位专家的评分结果按式(1)处理得到最终重要性评分axy,并建立对应的判断矩阵A, 如式(2)所示,计算判断矩阵最大特征值与特征向量,在经一致性检验后,得到换挡品质主观权重α=(αi).
| $ {a_{xy}} = \frac{{\sum\limits_{k = 1}^V {a_{xy}^k} - \max \left( {a_{xy}^k} \right) - \min \left( {a_{xy}^k} \right)}}{{V - 2}}, $ | (1) |
| $ \mathit{\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} 1&{{a_{12}}}&{{a_{13}}}& \ldots &{{a_{1n}}}\\ {1/{a_{12}}}&1&{{a_{23}}}& \ldots &{{a_{2n}}}\\ {1/{a_{13}}}&{1/{a_{23}}}&1& \ldots &{{a_{3n}}}\\ \vdots & \vdots & \vdots & \vdots & \vdots \\ {1/{a_{1n}}}&{1/{a_{2n}}}&{1/{a_{3n}}}& \ldots &1 \end{array}} \right]. $ | (2) |
式中:axy为第x项指标相对于第y项指标的最终重要性评分,axyk为第k位专家的第x项指标相对于第y项指标的重要性评分.
2.1.2 客观权重客观权重是数据中信息的真实反映,变异系数法正是直接利用各项指标中包含的信息以计算指标权重的一种方法,该方法认为取值差异越大的指标,即越难以实现的指标,更能反映被评价单位的差距.但传统变异系数法进行权重计算时,对于取值为负的指标是不适用的.因此考虑换挡品质评价的特点,对指标数据进行初始化,对m次换挡工况,n个评价指标数据组成的矩阵Fij,进行归一化处理,指标转换为dij,使其既能保留各指标值的排列信息,又实现转速梯度和负向冲击这两项指标符号的转变,并按照式(3)计算变异系数
| $ {\mathit{\boldsymbol{V}}_j} = \frac{{\sqrt {\frac{1}{{m - 1}}\sum\limits_{i = 1}^m {{{\left( {{d_{ij}} - \frac{1}{m}\sum\limits_{i = 1}^m {{d_{ij}}} } \right)}^2}} } }}{{\frac{1}{m}\sum\limits_{i = 1}^m {{d_{ij}}} }}, $ | (3) |
最终通过式(4)求得各指标客观权重βj:
| $ {\beta _j} = \frac{{{V_j}}}{{\sum\limits_{j = 1}^n {{V_j}} }}. $ | (4) |
综合权重需平衡好权重的客观性与主观性,本研究基于分配最优化原则,在加法组合赋权的基础上,建立综合权重向量与主客观权重向量的距离最小的目标函数,通过目标函数确定主观权重和客观权重的相对重要程度δ和η,使其既能体现数据反映的真实信息,又能充分考虑专家知识的重要性,系统科学地确定换挡品质评价指标的综合权重
| $ {w_j} = \delta \times {\alpha _j} + \eta \times {\beta _j}, $ |
主客观权重的相对重要程度求解公式为
| $ \begin{array}{*{20}{c}} {\min \sum\limits_{j = 1}^n {\left( {{{\left( {{w_j} - {\alpha _j}} \right)}^2} + {{\left( {{w_j} - {\beta _j}} \right)}^2}} \right),} }\\ {{\rm{ s}}{\rm{.t}}{\rm{. }}\sum\limits_j^n {{w_j}} = 1\quad ,\quad 0 \le {w_j} \le 1.} \end{array} $ |
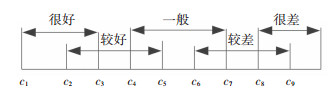
换挡品质的好与不好之间存在模糊性,而模糊综合评价通过一个模糊的集合来对结果进行全面评价,其特点是评价结果不绝对地肯定或否定,因此选择通过构建模糊综合评价模型进行换挡品质评价,其中模糊函数的确定是核心.为科学地建立模糊函数,考虑到数据的差异性,引入目标车型或者同类车型的测试参数,从中提取最优指标值p和最劣指标值q,对指标进行归一化.因为换挡品质的评价指标相邻评语之间的界限难以准确界定,所以本研究参考SAE评分标准与某整车厂自主知识体系,确定的换挡品质评价指标等级划分准则如表 2所示,换挡品质评价等级如表 3所示.考虑到界限的模糊性,加入模糊阈值θ将相邻评语等级界限设计为模糊区间,如图 4所示,模糊阈值θ的选取来自于试验车辆真实反应与标准的匹配程度.对SAE标准中的界进行归一化处理之后,分别向前向后拓展θ以确定模糊区间的界限ci,i=1, 2,…,10,且满足公式(5):
| 表 2 换挡品质评价指标等级划分准则表 Tab. 2 Cassification criteria for shift quality evaluation indexes |
| 表 3 换挡品质各评价等级描述 Tab. 3 Description of shift quality evaluation levels |
|
图 4 换挡品质评价指标模糊区间 Fig. 4 Fuzzy intervals of shift quality evaluation index |
| $ {c_{i + 1}} - {c_i} = \theta ,\quad i = 2,4,6,8. $ | (5) |
考虑到模糊阈值的存在,因此在F统计隶属度函数中选择正态分布,以实现模糊阈值范围内交叉隶属度的确定,最终建立的换挡品质指标的隶属度函数为
| $ {u_1} = \left\{ {\begin{array}{*{20}{c}} {1,}&{{c_1} < x < {c_2};}\\ {{e^{k{{\left( {x - {c_2}} \right)}^2}}},}&{{c_2} < x < {c_3};}\\ {0,}&{x > {c_3};} \end{array}} \right. $ |
| $ {u_2} = \left\{ {\begin{array}{*{20}{c}} {0,}&{x < {c_2};}\\ {{e^{k{{\left( {x - {c_3}} \right)}^2}}},}&{{c_2} < x < {c_3};}\\ {1,}&{{c_3} < x < {c_4};}\\ {{e^{k{{\left( {x - {c_4}} \right)}^2}}},}&{{c_4} < x < {c_5};}\\ {0,}&{x > {c_5};} \end{array}} \right. $ |
| $ {u_3} = \left\{ {\begin{array}{*{20}{c}} {0,}&{x < {c_4};}\\ {{e^{k{{\left( {x - {c_5}} \right)}^2}}},}&{{c_4} < x < {c_5};}\\ {1,}&{{c_5} < x < {c_6};}\\ {{e^{k{{\left( {x - {c_6}} \right)}^2}}},}&{{c_6} < x < {c_7};}\\ {0,}&{x > {c_7}.} \end{array}} \right. $ |
| $ {u_5} = \left\{ {\begin{array}{*{20}{c}} {0,}&{x < {c_8};}\\ {{e^{k{{\left( {x - {c_9}} \right)}^2}}},}&{{c_8} < x < {c_9};}\\ {1,}&{x > {c_9}.} \end{array}} \right. $ |
| $ {u_4} = \left\{ {\begin{array}{*{20}{c}} {0,}&{x < {c_6};}\\ {{e^{k{{\left( {x - {c_7}} \right)}^2}}},}&{{c_6} < x < {c_7};}\\ {1,}&{{c_7} < x < {c_8};}\\ {{e^{k{{\left( {x - {c_8}} \right)}^2}}},}&{{c_8} < x < {c_9};}\\ {0,}&{x > {c_9};} \end{array}} \right. $ |
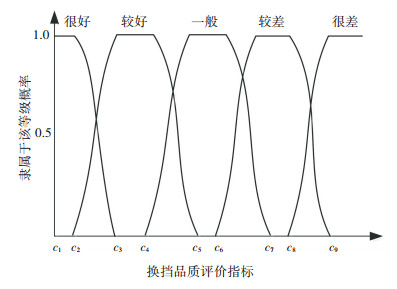
式中:ui∈[0, 1], (i=1, 2, ..., 5)是隶属于不同换挡品质等级的概率,x为线性归一化后的评价指标值,ci值为换挡品质评价指标模糊区间及界限,k为对应指标最优指标值p与最劣指标值q的中值.
隶属度函数曲线如图 5所示.
|
图 5 评价指标相对于各划分等级的隶属度函数 Fig. 5 Membership function of evaluation indexes corresponding to each classification level |
本研究针对DCT车辆换挡品质评价的特点,设计了完整的模糊综合评价算法,其流程如图 6所示.

|
图 6 模糊综合评价模型计算流程 Fig. 6 Calculation process of fuzzy comprehensive evaluation model |
其中包括以下步骤:
步骤1 测试参数清洗与指标识别.先对指标相关测试参数进行预处理,再对确定的评价指标通过识别方法进行识别;
步骤2 主观权重确定.针对确定的评价指标,通过结合德尔菲法和层次分析法获得判断矩阵,进行一致性检验之后获得主观权重α=(αj);
步骤3 客观权重确定.对评价指标归一化处理,采用变异系数法计算客观权重β=(βj);
步骤4 综合权重确定.基于综合权重与主客观权重距离最小的原则,计算得到兼顾数据差异性和主观性的综合权重W=(wj);
步骤5 一级评价权重确定.根据评价车辆的需求,确定动力性与平顺性的相对重要度r和1-r,建立一级评价权重W′=(r, 1-r);
步骤6 隶属度函数.在历史数据以及SAE标准的基础上,确定最优最劣指标值与模糊阈值,构建换挡品质评价指标动态隶属度函数,并计算模糊矩阵R=(uj)T;
步骤7 计算换挡品质评分.按照表 3得到的评分量化向量S=[9.0, 7.5, 6.0, 4.5, 3.0],计算换挡品质评分F=W·R·W′·S.
3 试验验证 3.1 试验设计为了验证本研究模糊综合评价的效果,以5种装配有DCT变速箱的紧凑型乘用车换挡数据为基础,提取评价指标中的最优和最劣指标值,并基于这5辆车的实际反映确定评价指标划分等级的模糊阈值,对另外两种装配有DCT的紧凑型乘用车Y1和Y2进行换挡品质评价.车辆Y1和Y2分别进行动力升档、动力降档、松油升档以及松油降档试验,试验数据主要采集整车CAN信号以及外接传感器信号,其中外接传感器包括IEPE加速度传感器以及SpeedBox速度传感器,利用Fire平台实现3个不同来源信号的同步采集,经过Vehicle spy软件进行数据读取.本文选取了Y1与Y2车的给油升档状况下4档升5档的10%~100%油门下的数据进行验证.为验证模型的有效性,在换挡试验过程中邀请5位专业主观评价人员分别对换挡过程整体以及动力性和平顺性单独进行重复10次评价,对评价结果进行数值处理,获得一组主观评分作为换挡品质评分真值.最后根据Y1与Y2车驾驶性需求,确定动力性与平顺性重要度分别为0.5与0.5.
3.2 验证结果讨论图 7是Y1和Y2车4挡升5挡动力升档不同评价方法的动力性换挡品质评分曲线,图 8是Y1和Y2车4挡升5挡动力升档换挡品质模糊综合评价模型评分曲线.无论是单纯的变异系数法还是模糊综合评价模型,Y1车和Y2车动力升档换挡过程的动力性评分结果表明:随着油门开度的增加,动力性评分逐渐提高,和车辆的实际反映是一致的;其次,运用模糊综合评价模型,Y1车的平顺性评分始终在动力性评分之上,这与Y1车以平顺性为设计基准,始终强调驾驶平顺性的设计概念是一致的;而Y2车在小油门开度下动力升档过程的平顺性得分较高,动力性相对较弱,在大油门下动力性评分则超越了平顺性得分,在实车上体现为动力推背感好,但有较为强烈的抖动和冲击,验证了模糊综合评价模型和变异系数法在换挡品质评价中的有效性.

|
图 7 4挡升5挡动力升档的动力性换挡品质评分 Fig. 7 Dynamic shift quality scores of power upshift from fourth gear to fifth gear |
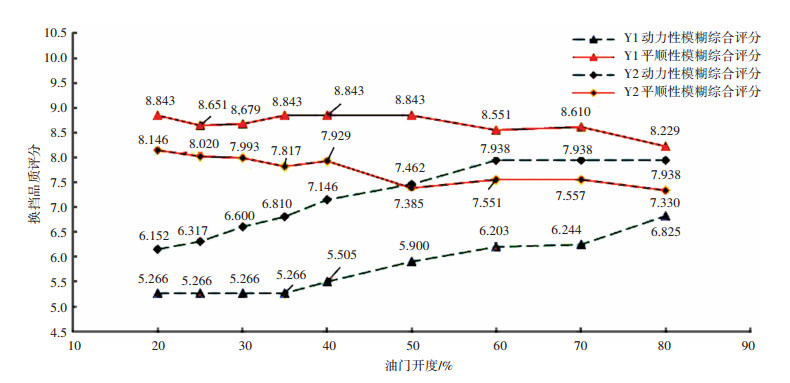
|
图 8 4挡升5挡动力升档的模糊综合评价评分比较 Fig. 8 Comparison of fuzzy comprehensive evaluation scores of power upshift from fourth gear to fifth gear |
在试验过程中,为获取准确的换挡品质,已邀请了5位专业主观评价人员分别重复进行10次换挡品质评价,即便是专业的主观评价人员也难以避免主观评价的缺陷,因此只比较模糊综合评价评分结果与获得的换挡品质评分真值,不做模糊综合评价与主观评价具体的准确性比较.同时上文验证了模糊综合评价模型与只运用变异系数法在换挡品质评价上的有效性,还需验证模糊综合评价模型相对于单纯变异系数法的准确性.通过2.3节的计算流程可得到Y1与Y2车的综合权重以及最终的换挡品质评分,表 4描述了Y1和Y2的动力升档4挡升5挡换挡品质评分.为比较模糊综合评价模型结果与单纯变异系数法的结果,分别引入了最大偏差和person相关系数作为比较指标,结果表明,变异系数法在Y1和Y2车的换挡品质评分最大偏差分别为0.358和0.342,模糊综合评价模型的最大偏差分别为0.171和0.184,模糊综合评价模型的效果要明显优于单纯的变异系数法结果.通过person相关系数计算,模糊综合评价模型与真实评分的person相关系数分别为0.926和0.946,变异系数法与真实评分的person相关系数分别为0.915和0.870,评价结果表明模糊综合评价更为准确.
| 表 4 4挡升5挡动力升挡换挡品质评分 Tab. 4 Shift quality scores of power upshift from fourth gear to fifth gear |
动力升档过程中的各升挡过程二级指标综合权重如表 5所示,运用模糊综合评价模型揭示了动力性二级评价指标中转速梯度权重占比达到41.3%,在动力性中影响最大;平顺性二级评价指标中离合器接合加速度幅值占比达到27.6%,对平顺性影响最大,最终结果可以用于指导该车型如何完善换挡品质.
| 表 5 动力升档各二级指标权重 Tab. 5 Secondary index weight of power upshift |
1) 从整车信号中的时间、纵向加速度以及发动机转速3个维度确定了影响换挡品质的10个指标,并通过层次聚类与专家经验相结合的方法系统科学地实现了换挡品质评价指标体系的构建.
2) 将层次分析法与变异系数法计算的主客观权重结合,确定了换挡品质评价指标的综合权重;并基于数据差异性和模糊阈值,建立了换挡品质评价指标的隶属度函数.
3) 通过综合权重和隶属度函数最终构建了换挡品质模糊综合评价模型,并通过试验验证了该方法相对于单纯客观评价方法的有效性和准确性,能对换挡品质改善提出有效的指导.
| [1] |
王健, 雷雨龙, 郭孔辉, 等. 车辆换档质量概念的完善与评价[J]. 吉林大学学报(工学版), 2007(5): 1014. WANG Jian, LEI Yulong, GUO Konghui, et al. Concept improvement and assessment on vehicle gear shift quality[J]. Journal of Jilin University(Engineering and Technology Edition), 2007(5): 1014. DOI:10.13229/j.cnki.jdxbgxb2007.05.027 |
| [2] |
何宁, 赵治国, 李瑜婷. 双离合器自动变速器换挡规律及其仿真评价[J]. 中国机械工程, 2011, 22(3): 367. HE Ning, ZHAO Zhiguo, LI Yuting. Shift schedule and simulation evaluation for dual clutch automatic transmission[J]. China Mechanical Engineering, 2011, 22(3): 367. |
| [3] |
马宗正, 马建辉. 换挡转速对公交车辆油耗的影响分析[J]. 合肥工业大学学报(自然科学版), 2014, 37(5): 530. MA Zongzheng, MA Jianhui. Influence of engine shift speed on fuel consumption of public transport vehicle[J]. Journal of Hefei University of Technology(Natural Science), 2014, 37(5): 530. DOI:10.3969/j.issn.1003-5060.2014.05.005 |
| [4] |
胡健, 汪韶杰. 一种新型双离合自动变速器的换挡品质研究[J]. 农业装备与车辆工程, 2013, 51(12): 35. HU Jian, WANG Shaojie. Study on shift quality of a new type dual clutch automatic transmission[J]. Agricultural Equipment & Vehicle Engineering, 2013, 51(12): 35. DOI:10.3969/j.issn.1673-3142.2013.12.010 |
| [5] |
陈玉华.离合器接合抖动的测试、分析与评价[D].广州: 华南理工大学, 2013 CHEN Yuhua.Test, analysis and evaluation of clutch engagement jitter[D]. Guangzhou: South China University of Technology, 2013 http://cdmd.cnki.com.cn/Article/CDMD-10561-1014151506.htm |
| [6] |
刘永刚.轿车双离合器自动变速系统综合匹配控制研究[D].重庆: 重庆大学, 2010 LIU Yonggang.Study on integrated control of passenger vehicles equipped with dual clutch transmissions[D].Chongqing: Chongqing University, 2010 http://cdmd.cnki.com.cn/Article/CDMD-10611-2010215513.htm |
| [7] |
雷雨龙, 刘科, 付尧, 等. 基于理想换挡过程的换挡品质评价模型[J]. 吉林大学学报(工学版), 2015, 45(2): 358. LEI Yulong, LIU Ke, FU Yao, et al. Shift quality evaluation model based on ideal shift process[J]. Journal of Jilin University(Engineering and Technology Edition), 2015, 45(2): 358. |
| [8] |
孙贤安, 吴光强. 双离合器式自动变速器车辆换挡品质评价系统[J]. 机械工程学报, 2011, 47(8): 146. SUN Xianan, WU Guangqiang. Shifting quality evaluation system for dual clutch transmission vehicle[J]. China Mechanical Engineering, 2011, 47(8): 146. |
| [9] |
宋世欣, 张元侠, 刘科, 等. 双离合器自动变速器控制品质评价指标分析[J]. 汽车工程, 2015, 37(8): 925. SONG Shixin, ZHANG Yuanxia, LIU Ke, et al. An analysis on the evaluation metrics of control quality for vehicles with dual clutch transmission[J]. Automotive Engineering, 2015, 37(8): 925. DOI:10.19562/j.chinasae.qcgc.2015.08.011 |
| [10] |
王尔烈, 王显会, 陈慧岩, 等. 大功率自动变速器换挡离合器调压控制研究[J]. 中国公路学报, 2018, 31(3): 151. WANG Erlie, WANG Xianhui, CHEN Huiyan, et al. Investigation on pressure control of shifting clutch for high-power automatic transmission[J]. China Journal of Highway and Transport, 2018, 31(3): 151. DOI:10.19721/j.cnki.1001-7372.2018.03.017 |
| [11] |
MIN G, SON H, SONG M, et al. Development of a gear fork control algorithm to improve the shift quality of a dual-clutch transmission[J]. Journal of Automobile Engineering, 2016, 230(11): 1477. DOI:10.1177/0954407015613266 |
| [12] |
PARK J, AHN S, KWON O, et al. Development of 2 stage CVT shift control algorthm to reduce torque variation during 1-2 upshift of planetary gear[J]. ASME, 2012, 6: 389. DOI:10.1115/DETC2012-70853 |
| [13] |
SHIN B K, HAHN J O, YI K, et al. A supervisor-based neural-adaptive shift controller for automatic transmissions considering throttle opening and driving load[J]. KSME International Journal, 2000, 14(4): 418. DOI:10.1007/BF03186435 |
| [14] |
王延忠, 汪大鹏, 李圆, 等. 多态模块化自动变速器换挡过程仿真与试验[J]. 哈尔滨工业大学学报, 2018, 50(7): 103. WANG Yanzhong, WANG Dapeng, LI Yuan, et al. Simulation and test on shift process of multi-state modular automatic transmission[J]. Journal of Harbin Institute of Technology, 2018, 50(7): 103. DOI:10.11918/j.issn.0367-6234.201710036 |
| [15] |
付尧.基于客观评价的双离合器自动变速器换挡控制技术研究[D].长春: 吉林大学, 2015 FU Yao.Research on gearshift control for dual clutch transmission based on objective evaluation[D]. Changchun: Jilin University, 2015 |
| [16] |
高炳钊, 洪金龙, 陈虹. 汽车传动系统平顺性驾驶品质控制[J]. 控制理论与应用, 2017, 34(7): 849. GAO Bingzhao, HONG Jinlong, CHEN Hong. Drivability control of automotive drivetrain[J]. Control Theory & Applications, 2017, 34(7): 849. |
| [17] |
曲建华, 孟宪林, 尤宏. 地表水源突发污染应急处置技术筛选评估体系[J]. 哈尔滨工业大学学报, 2015, 47(8): 54. QU Jianhua, MENG Xianlin, YOU Hong. Evaluation system for emergency disposal technology insurface drinking watersource pollution[J]. Journal of Harbin Institute of Technology, 2015, 47(8): 54. |
 2020, Vol. 52
2020, Vol. 52


