2. 长安大学 公路学院,西安 710064;
3. 苏州科技大学 土木工程学院,江苏 苏州 215011
2. School of Highway, Chang'an University, Xi'an 710064, China;
3. School of Civil Engineering, Suzhou University of Science and Technology, Suzhou 215011, Jiangsu, China
立交是山区高速公路或公路网实现交通流转换的构造物,当高速公路与一般公路交叉,驶出及驶入立交区域时常采用平面交叉的型式,典型的立交有收费菱形立交,只需要设置唯一收费站,即可实现枢纽功能.收费菱形立交一侧设置左转弯,另外一侧设置右转弯,为了节约用地,通常交叉口与上跨桥梁距离很近,驾驶员行驶至交叉口附近时,前方大型车辆容易影响小型车驾驶员对交叉口信息的获取,形成交通信息识别盲区.同时,由于立交区信息瞬息万变引起交通识别问题进而导致事故频发,准确预测动态交通量获取交通信息识别概率已成为立交区域安全管理的重要手段之一.
近年来,对交通信息识别问题主要集中在两个方面:一方面利用深度学习法研究高速公路中交通信息识别问题,文献[1-3]提出了一种短期(KNN)和长短期记忆网络(LSTM)的时空交通流KNN-LSTM模型,运用深度学习法研究交通信息的探测技术,建立了多车道高速公路路侧交通信息识别模型;另一方面,运用神经网络方法对实时交通流数据进行聚类分析,将神经网络模型与无迹卡尔曼滤波方法结合,同时融合交互式方法实现交通信息识别预测[4-5],文献[6]基于时间及空间研究了交通信息识别问题,文献[7]对交通信息的视认距离及大小型车之间的速度差、车头时距等方面进行研究,确定交通信息设置方法.以上研究大多针对高速公路路侧交通信息识别问题,对立交区域交叉口交通信息识别问题研究较少,同时已有问题主要针对静态、单一的交通量状态,对交通信息视认区域、交通信息识别预测的定义相对保守,致使静态交通识别概率的计算结果与实际识别过程存在偏差.
事实上,立交区域交叉口信息识别预测与交通信息的获取、交通量的周期性动态变化有直接关系[8-9].每个周期的交通量时间序列具有一定的相似性,且包含多种周期,如1 d(24 h)、5 d(120 h)、7 d (168 h)、28 d(672 h)之间有相似重复性规律和趋势[10],但在某些情况下也具有一定的随机性.因此,交通流信息可认为是长期及短期的时间周期项和交通量趋势项及交通流辅助项(路网节点指数项、交通量随机变化项)综合构成[11-13].
本文通过建立驾驶员信息识别框架,形成考虑驾驶员特性及预测交通量的识别视距计算方法,运用时间序列对动态交通量进行预测,形成交通信息识别预测模型,旨在对主线上跨的立交区域交叉口交通信息设置及管理提供依据.
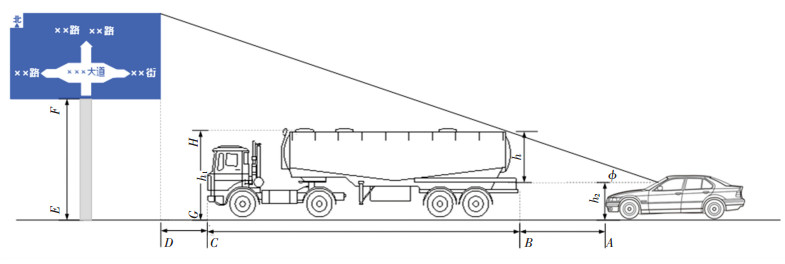
1 交通信息识别框架模型交通信息设置应考虑交叉口信号、驾驶员对交通信息的识别及交通信息安装位置的合理性[14].车辆驶入交叉口区域,当小型车前方有大型车时,应考虑前方大型车辆对交通信息的识别问题,其构成如图 1所示.
|
图 1 交通信息识别示意图 Fig. 1 Schematic diagram of traffic sign recognition |
小型车辆驾驶员视线高度与交通信息高度差记为h(h=h1-h2),交通信息与小型车水平视线高度夹角为ϕ[15],文中ϕ取15°,驾驶员视角超过此阈值时,交通信息容易被错过,如图 1所示,则根据几何关系,可得
| $ D > \frac{h}{{{\rm{tan}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \phi }}. $ | (1) |
其中D为交通信息发现点与交通信息间的距离,m.
由几何关系可知:在一定环境条件下可根据动态交通量和驾驶员视距确定,因此,上述不等式中主要为水平视线与交通信息间的夹角问题,与驾驶员对交通信息的识别及动态交通量有关.因此有必要解决驾驶员在行驶过程中的交通信息识别问题.
2 识别视距计算分析立交区域主线上跨交叉口前一段范围内,驾驶员主要工作任务是对道路环境引起的视觉混乱或对潜在交通信息源进行判断,选择合理的措施以安全高效地完成行驶任务[16].
2.1 条件假设立交区域交叉口中小型车驾驶员对交通信息识别受前方大型车辆或主线上跨桥梁共同作用的影响,与大型车混入率、交通量等相关,同时也与大型车和小型车车头时距有关,其中,动态交通量及交通组成对交通信息识别起到重要影响,因此,交通信息识别预测时应充分考虑交通量预测,拟作以下假设:1)交叉口附近为直线段,且该区域最大纵坡不大于3%;2)小型车、中型车、大型车按设计规范要求;3)交通信息设置满足设施设计规范要求;4)各种车型车辆到达率服从泊松分布,大型车在小型车前方的概率为50%;5)立交区域交叉口主要有小型车、中型车及大型车3种车型,其比例分别为i1,i2,i3.
2.2 动态识别视距计算驾驶员对交通信息处理通常需要经过读取信息、判断信息、操作车辆(减速、加速、转向、直行)等过程[17].动态识别视距为驾驶员发现交通信息至完成相应操作且车辆与前方交通信息保持一定的安全距离(I),如图 2所示.

|
图 2 识别视距示意图 Fig. 2 Schematic diagram of recognition distance |
交通信息设置在E点,车辆按图中方向行驶至交叉口A点时,发现E点的交通信息,此段时间驾驶员对交通信息进行识别,B点开始读取交通信息,至C点完成交通信息读取,车辆在此段时间所经过的距离称之为认读距离(l′);当驾驶员认读完信息后根据交叉口道路交通条件作相应决策,车辆行驶至D点,此段过程车辆经过的距离称为判断距离(j);从行动点D至动作完成点F称之为行动距离(l);s为与前方车辆之间的安全距离,如图 2所示.驾驶员读完交通信息,在动态交通环境下安全、顺畅地完成必要驾驶行为(如:变换车道、减速行驶等)所经过的距离为动态识别视距[18],因此,动态识别视距计算公式为
| $ {L_s} = {l^\prime } + j + l + s, $ | (2) |
式中:
| $ \begin{array}{*{20}{c}} {{l^\prime } = v \cdot {t_1},}\\ {j = v \cdot {t_2},}\\ {l = {u_{a0}}({\tau _1}^\prime + {\tau _1}^{\prime \prime }) + \frac{1}{{3.6}}({\tau _2}^\prime + \frac{{{\tau _2}^{\prime \prime }}}{2}){u_{a0}} + }\\ {\frac{{{u_{a0}}^2}}{{25.92{a_{{\rm{max}}}}}} - \frac{{{u_{s0}}^2}}{{25.92{a_{{\rm{max}}}}}}.} \end{array} $ | (3) |
其中:t1为认读时间,即驾驶员对交通信息的读取过程,通常取3 s;t2为判断时间,即驾驶员对交通信息的研判过程(与驾驶员心理有关),通常取2 s;ua0为立交区域交叉口车辆运行速度,可按交叉口设计速度取值, m/s;us0为车辆经过研判后的速度,可以通过预测动态交通量与运行速度获得[19].
当τ2 ″2→0时,
动态识别视距的获得与动态交通环境密切相关,要想获得较为准确动态识别视距,必须在考虑现有交通量及交通组成条件下,获取具有时间序列的长期和短期预测交通量.
3 时间序列的交通量预测立交区域由于各种交通量与影响因素之间相互作用,各交通组成中也存在相互制约关系,交通量的变化具有随机性,非线性特点,其影响因素也具有一定的随机性、非线性特征,因此,交通量的形成通常不能用简单的数学表述.立交区域车辆速度、交通量具有时间特性的分布规律[23],合理利用时间序列对交通量预测,可有效解决交叉口由于交通量随时间变化导致的交通信息获取不足问题.
长期和短期时间序列(long and short-term time-series,LST)预测模型是解决时间序列导致的交通问题[24]. LST使用卷积神经网络(convolution neural network, CNN)与递归神经网络(recurrent neural networks,RNN)将当前交通量与时间序列联系起来,建立时间序列交通量Q(t),其分解为主要项为时间周期项q(t)及交通量趋势项f(t),辅助项为路网节点指数项ψ(t)及交通量随机变化项ε(t).
根据预测时间序列中t时刻内的交通量具有重复性特点,可运用三次指数平滑法预测交通量主要项q(t)+f(t),预测交通量主要项为
| $ \begin{array}{*{20}{l}} {\hat q(t) + \hat f(t) = {\theta _1}(t){{\hat G}_1}(t) + {\theta _2}(t){{\hat G}_2}(t) + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\theta _3}(t){{\hat G}_3}(t) + {\theta _4}(t){{\hat G}_4}(t).} \end{array} $ | (4) |
式中:θi(t)为权重指数;
| $ {\hat G_i}(t) = {s_i}(t) + h \cdot {t_i} + {r^j}_{i - k + h}. $ | (5) |
其中:
| $ {s_i}(t) = \alpha ({G_i}(t) - {p_{i - k}}) + (1 - \alpha )({s_{i - 1}}(t) + {t_{i - 1}}), $ | (6) |
| $ {{t_i} = \beta ({s_i}(t) - {s_{i - 1}}(t)) + (1 - \beta ){t_{i - 1}},} $ | (7) |
| $ {r_i^j = \gamma ({G_i}(t) - {s_i}) + (1 - \gamma ){p_{i - k}}.} $ | (8) |
式中:i为季节性影响因子;k为周期长度;si(t)为时间步长i(第i个时间点)上经过平滑后的值;ti为当前趋势的未平滑值,是当前平滑值(si(t))和上一个平滑值(si-1(t))的时间差;ri为立交区域交叉口交通量变化周期;α,β,γ为平滑常数;Gi(t)为真实值.
| $ \begin{array}{*{20}{l}} {\mathit{\boldsymbol{\theta }}(t + 1) = \mathit{\boldsymbol{\theta }}(t) + }\\ {\;\:\frac{{\mathit{\boldsymbol{p}}(t)\mathit{\boldsymbol{\varphi }}(t + 1)[\mathit{\boldsymbol{Q}}(t) - {\mathit{\boldsymbol{\varphi }}^{\rm{T}}}(t + 1)\mathit{\boldsymbol{\theta }}(t)]}}{{\lambda + {\mathit{\boldsymbol{\varphi }}^{\rm{T}}}(t + 1)\mathit{\boldsymbol{p}}(t)\mathit{\boldsymbol{\varphi }}(t + 1)}},} \end{array} $ | (9) |
| $ {\mathit{\boldsymbol{p}}(t + 1) = \frac{{\mathit{\boldsymbol{p}}(t)}}{\lambda }[\mathit{\boldsymbol{E}} - K(t + 1){\mathit{\boldsymbol{\varphi }}^{\rm{T}}}(t)],} $ | (10) |
| $ {K(t + 1) = \frac{{\mathit{\boldsymbol{p}}(t){\mathit{\boldsymbol{\varphi }}^{\rm{T}}}(t + 1)}}{{\lambda + {\mathit{\boldsymbol{\varphi }}^{\rm{T}}}(t + 1)\mathit{\boldsymbol{p}}(t)\mathit{\boldsymbol{\varphi }}(t + 1)}}.} $ | (11) |
式中:λ为遗忘因子,0 < λ < 1;p (t)为误差协方差矩阵.
以一个月内的预测为基本量,分别按照24、120、168、720 h为周期进行预测,则
| $ \mathit{\boldsymbol{\theta }}(t) = {\left[ {\begin{array}{*{20}{l}} {{\theta _1}(t)}&{{\theta _2}(t)}&{{\theta _3}(t)}&{{\theta _4}(t)} \end{array}} \right]^{\rm{T}}}, $ | (12) |
| $ \mathit{\boldsymbol{\varphi }}(t) = {\left[ {\begin{array}{*{20}{l}} {{{\hat G}_1}(t)}&{{{\hat G}_2}(t)}&{{{\hat G}_3}(t)}&{{{\hat G}_4}(t)} \end{array}} \right]^{\rm{T}}}. $ | (13) |
路网节点预测交通量
运用STARIMA模型[25],W(h)交通流中节点权重,路网指数项
| $ \hat \psi (t) = {W^{(h)}} = \sum\limits_{j = 1}^K {w_{ij}^{(h)}} {x_j}(t). $ | (14) |
式中wij(h)为路网空间权重矩阵中路段i和路段j之间的权值,满足:
| $ \sum\limits_{j = 1}^K {w_{ij}^{(h)}} = 1. $ | (15) |
因此,由时间及空间相关性引起的交通节点的路网指数项交通量为
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \psi (t) = \hat \psi (t) = \\ \frac{{\sum\limits_{i = 1}^N {\sum\limits_{j = 1}^K {w_{ij}^l} } {x_j}(t)w_{ij}^l{x_j}(t + \Delta t)}}{{\sqrt {\sum\limits_{i = 1}^N {\sum\limits_{i = 1}^T {(w_{ij}^l{x_j}(} } t){)^2} + \sum\limits_{i = 1}^N {\sum\limits_{i = 1}^T {(w_{ij}^l{x_j}(} } t + \Delta t){)^2}} }}. \end{array} $ | (16) |
基于此,可获得立交区域交叉口中预测交通量主要项及辅助项值:
| $ \begin{array}{l} \begin{array}{*{20}{l}} {Q(t) = {\theta _1}(t){{\hat G}_1}(t) + {\theta _2}(t){{\hat G}_2}(t) + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\theta _3}(t){{\hat G}_3}(t) + {\theta _4}(t){{\hat G}_4}(t) + } \end{array}\\ \frac{{\sum\limits_{i = 1}^N {\sum\limits_{j = 1}^K {w_{ij}^l} } {x_j}(t)w_{ij}^l{x_j}(t + \Delta t)}}{{\sqrt {\sum\limits_{i = 1}^N {\sum\limits_{i = 1}^T {(w_{ij}^l{x_j}(} } t){)^2} + \sum\limits_{i = 1}^N {\sum\limits_{i = 1}^T {(w_{ij}^l{x_j}(} } t + \Delta t){)^2}} }} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \varepsilon (t). \end{array} $ | (17) |
交通信息识别是由动态识别视距及预测交通量共同决定的,文中拟通过动态识别视距及交通预测结果对其识别问题进行预测.
小型车在A点至B点范围内与前方大车距离小于AB长度时,驾驶员不能准确识别交通信息.由2.1节假设知,大型车出现在AC区域,小汽车出现在大型车辆之后,交通信息识别预测可分为3个方面.
4.1 内侧车道交通信息识别概率预测假设双车道匝道进入交叉口的一定长度范围内的交通量密度为λ表示为
| $ \lambda = \frac{{Q(t)}}{V}, $ | (18) |
则在理想条件下AC长度内大型车在小型车前数量为ω·AC,其中
| $ \omega = \frac{{0.5\lambda {i_3}}}{{({i_1} + {i_2} + {i_3})}}, $ | (19) |
则在此区域大型车引起小型车识别问题概率为
| $ {p_1} = 1 - p(k = 0) = 1 - {(\omega \cdot \overline {AC} )^0}{{\rm{e}}^{ - \tau \omega \cdot \overline {AC} }}. $ | (20) |
立交区域交叉口中各车道车型分布与交通量、左转弯车道设置、右转弯车道设置等因素相关,当交叉口区域交通流处于稳定流或自由流状态时,车辆在车道中的分布与车速差相关,小型车速度较高,大型车速度较低,同时大型车驾驶员习惯在外侧车道行驶,外侧车道大车占有率可按正常车道的τ倍计算,设内侧车道在AC长度内大型车占有率为τ·λ·AC,则出现交通信识别的概率为
| $ {p_2} = 1 - p(k = 0) = 1 - {(\tau \cdot \omega \cdot \overline {AC} )^0}{{\rm{e}}^{ - \tau \cdot \omega \cdot \overline {AC} }}. $ | (21) |
小型车在AB区域内的外侧车道,大型车出现在BC区域内,发生交通信息识别问题的概率为
| $ \begin{array}{*{20}{l}} {{p_3} = 2[1 - p(k = 0)] = }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 2[1 - {{(\tau \cdot \omega \cdot \overline {AB} )}^0}{{\rm{e}}^{ - \tau \cdot \omega \cdot \overline {AB} }}].} \end{array} $ | (22) |
由以上分析知,设在AB长度内有一辆以上小型车的事件为J1,小型车在外侧车道行驶,在AC长度内没有大车事件为J2,小型车在内侧车道行驶,在AC区域内不出现大型车的事件为J3,在此区域内小型车不存在识别问题,准确获取交通信息概率为
| $ P = P[{J_1} \cap ({J_2} \cup {J_3})] = {P_1} \cdot ({P_2} + {P_3} - {P_2} \cdot {P_3}). $ | (23) |
其中P1、P2、P3与立交区域交叉口附近车辆运行速度、驾驶员特性、预测交通量等因素相关.
5 仿真实验与结果分析 5.1 实验数据采集本实验采集了2018年5月21日至2018年6月20日浙江、陕西,以及2019年2月11日至2019年3月10日澳大利亚墨尔本共两个月中12座主线上跨桥梁的立交数据,匝道为双车道出入口,交叉口为单向双车道,运行速度为实测数据,年平均日交通量实测获得,各种车型到达率服从泊松分布,大型车在内外侧车道所占比重按实际调研所得,交通流统计时间间隔为15 min,数据见表 1.表中v1为在交叉口前实测车辆速度;v2为距离交叉口100 m减速后实测速度.
| 表 1 立交调研数据 Tab. 1 Survey data of intersection of interchanges |
借助于SIMULINK及MATLAB2019软件,以动态识别视距的计算方法及基于时间序列的交通量信息识别预测模型预测立交区域交叉口交通量.大型车、中型车、小型车的比例为4:3:3;运行速度按设计速度85%计算;时间间隔采用15 min序列,运用三次季节性指数平滑法预测时采用1 d作为一周期,即s1(t)=96,可得α1、β1、γ1,同样s2(t)=480,可得α2、β2、γ2,同样s3(t)=672,可得α3、β3、γ3,同样s4(t)=2 688,可得α4、β4、γ4,从t>96开始对其三次平滑预测,以实测4周中的第3周作为预测值与实测值比对分析.由于速度与交通信息识别概率之间具有较大的相关性,采用速度作为划分参数依据,即
| $ {\alpha _1} = {v_{{\rm{min}}}} + \frac{{(o(h) - 0.5)({v_{{\rm{max}}}} - {v_{{\rm{min}}}})}}{H}. $ | (24) |
式中:ο(h)为1,2,…, H;vmin、vmax分别为在立交区域交叉口中的速度最大值和最小值.
参数
| $ \begin{array}{*{20}{l}} {\left[ {{\alpha _1}^\prime - \frac{{({v_{{\rm{max}}}} - {v_{{\rm{min}}}})}}{{(H \cdot \bar v)}},{\alpha _1}^\prime + \frac{{({v_{{\rm{max}}}} - {v_{{\rm{min}}}})}}{{(H \cdot \bar v)}}} \right],}\\ {\left[ {{\beta _1}^\prime - \frac{{({v_{{\rm{max}}}} - {v_{{\rm{min}}}})}}{{(H \cdot \bar v)}},{\beta _1}^\prime + \frac{{({v_{{\rm{max}}}} - {v_{{\rm{min}}}})}}{{(H \cdot \bar v)}}} \right],}\\ {\left[ {{\gamma _1}^\prime - \frac{{({v_{{\rm{max}}}} - {v_{{\rm{min}}}})}}{{(H \cdot \bar v)}},{\gamma _1}^\prime + \frac{{({v_{{\rm{max}}}} - {v_{{\rm{min}}}})}}{{(H \cdot \bar v)}}} \right].} \end{array} $ |
其中
| $ \bar v = \frac{{({v_{{\rm{max}}}} + {v_{{\rm{min}}}})}}{2}. $ | (25) |
计算其中间值与预测值和实际值之间的平均绝对误差,当其值小于5%时,可取该值作为α1、β1、γ1值,其他按此方法计算.
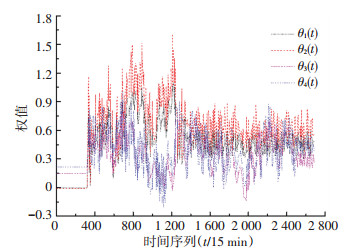
5.2.1 预测权值可靠性分析采用带遗忘因子计算权重时, 遗忘因子λ取值一般为0.95~0.99,文中取中值,即λ=0.97,θi(t)=[0 0 0 0]T,i分别取1,2,3,4,如图 3所示.星期一到星期五中θ1(t)和θ2(t)基本保持一定趋势,在星期六与星期日之间θ3(t)明显高于θ1(t)及θ2(t),说明周末的交通趋势与周一至周五具有差异性,θ4(t)在每星期六与星期日有相对下降趋势,表明星期六及星期日对星期一至星期五交通量依赖程度较大,因此,文中采用了4种权重,基本涵盖了交通量预测过程中每个节点的变化,具有一定的合理性.
|
图 3 权重关系 Fig. 3 Weight relations |
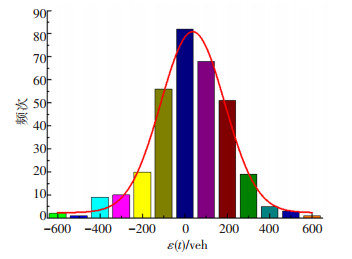
运用组合预测法对28 d时间序列中的1周(168 h)交通流量随机项进行预测,共有2 688时间预测节点,327个随机项预测值,交通量随机项频次预测误差,如图 4所示.该随机项误差服从正态分布,说明在时间序列条件下随机项对全局交通信息识别概率影响不大.
|
图 4 随机项组合频率分布 Fig. 4 Combination frequency distribution of random items |
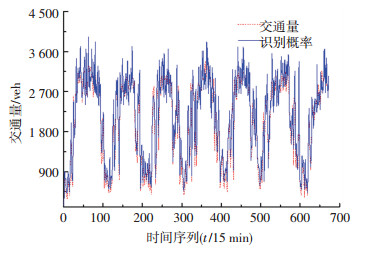
由于在28 d中的第3周相关性较为明显,运用MATLAB采用第3周作为基准进行预测,预测时间序列交通量与车辆识别概率虽然在第300~400时间序列区间识别概率与交通量有偏差,但总体趋于一致, 具有较好的相关性,如图 5所示.
|
图 5 交通量与识别概率相关性 Fig. 5 Correlation between traffic volume and recognition probability |
运用交通信息识别概率模型对时间序列交通信息识别概率预测值和真实值贴合度进行比较,通过平均绝对误差MAD,均方根误差RMSE及均方差MSE评价预测结果的准确性,运用泊松回归相关性系数得出预测值与实测值间的相关系数为0.849,说明实测值与预测值具有较好的相关性.
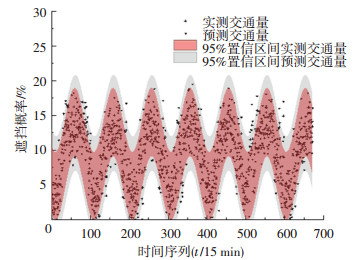
为了进一步阐明预测结果和实测值的相关性,运用Image J及Origin数字图像处理法对交通信息识别概率实测值95%置信区间和预测值95%置信区间对比,确定两者在95%置信区间内的相关性,根据计算得到两者重叠部分为87.65%,预测结果如图 6所示,预测结果比实测结果具有更好的广泛性和可靠性.
|
图 6 基于时间序列的识别概率预测结果 Fig. 6 Recognition probability prediction results based on time series |
1) 提出考虑驾驶员视觉的交通信息识别概率模型.运用动态预测交通量修正模型,获取动态识别视距值.
2) 运用交通量预测模型及卷积神经网络理论对立交区域交叉口交通量进行短期15 min及长期28 d时间序列预测,分析预测交通量与交通信息识别概率相关性.
3) 交通量预测结果显示,交通信息识别存在问题区域,可从提高驾驶员视认距离角度出发,采用立交区域交叉口交通信息灵活性设置.
4) 在仿真过程中对大型车混入比例进行了初步假设,也可根据实际的交通组成进行计算,以指导立交区域交叉口交通信息设置.
| [1] |
胡绍荣, 马荣国, 李苗苗, 等. 多车道高速公路路侧交通标志遮挡概率研究[J]. 中国公路学报, 2018, 31(3): 116. HU Shaorong, MA Rongguo, LI Miaomiao, et al. Study on blocking probability of traffic signs on multi-lane expressway[J]. China Journal of Highway and Transport, 2018, 31(3): 116. DOI:10.19721/j.cnki.1001-7372.2018.03.013 |
| [2] |
QIAN Rongqiang, LIU Qianyun, YUE Yong, et al. Road surface traffic sign detection with hybrid region proposal and fast R-CNN[C]//Proceedings of 12th International Conference on Natural Computation, Fuzzy Systems and Knowledge Discovery (ICNC-FSKD). Piscataway, NJ: IEEE, 2016: 555. DOI: 10.1109/FSKD.2016.7603233
|
| [3] |
XU Dongwei, WANG Yongdong, PENG Peng, et al. Real-time road traffic state prediction based on kernel-KNN[J]. Transportmetrica A: Transport Science, 2020, 16(1): 104. DOI:10.1080/23249935.2018.1491073 |
| [4] |
唐智慧, 郑伟皓, 董维, 等. 基于交互式BP-UKF模型的短时交通流预测方法[J]. 公路交通科技, 2019, 36(4): 117. TANG Zhihui, ZHENG Weihao, DONG Wei, et al. Short-term traffic flow prediction method based on interactive BP-UKF model[J]. Highway Transportation Technology, 2019, 36(4): 117. DOI:10.3969/j.issn.1002-0268.2019.04.017 |
| [5] |
邓亚娟, 李苗苗, 胡小霞, 等. 多车道高速公路门架式交通标志遮挡概率研究[J]. 公路, 2018(4): 179. DENG Yajuan, LI Miaomiao, HU Xiaoxia, et al. Study on occlusion probability of multi-lane highway gantry traffic signs[J]. Highway, 2018(4): 179. DOI:10.1016/j.aap.2018.07.014 |
| [6] |
AGARWAL V, CHAKROBORTY P. Stochastic analysis of the duration of occlusion of an overhead sign by a leading heavy vehicle: application to sign design[J]. Journal of Transportation Engineering, 2014, 140(8): 04014036. DOI:10.1061/(ASCE)TE.1943-5436.0000693 |
| [7] |
COSTA M, SIMONE A, VIGNALI V, et al. Fixation distance and fixation duration to vertical road signs[J]. Applied Ergonomics, 2018, 69: 48. DOI:10.1016/j.apergo.2017.12.017 |
| [8] |
GE W, CAO Y, DING Z, et al. Forecasting model of traffic flow prediction model based on multi-resolution SVR[C]// Proceedings of the 3rd International Conference on Innovation in Artificial Intelligence. New York: ACM, 2019: 1. DOI: 10.1145/3319921.3319923
|
| [9] |
ZHOU T, JIANG D, LIN Z, et al. Hybrid dual Kalman filtering model for short-term traffic flow forecasting[J]. IET Intelligent Transport Systems, 2019, 13(6): 1023. DOI:10.1049/iet-its.2018.5385 |
| [10] |
MA T, ANTONIOU C, TOLEDO T. Hybrid machine learning algorithm and statistical time series model for network-wide traffic forecast[J]. Transportation Research Part C: Emerging Technologies, 2020, 111: 352. DOI:10.1016/j.trc.2019.12.022 |
| [11] |
KONG F, LI J, JIANG B, et al. Short-term traffic flow prediction in smart multimedia system for internet of vehicles based on deep belief network[J]. Future Generation Computer Systems, 2019, 93: 460. DOI:10.1016/j.future.2018.10.052 |
| [12] |
VLAHOGIANNI E I, KARLAFTIS M G, GOLIAS J C. Optimized and meta-optimized neural networks for short-term traffic flow prediction: a genetic approach[J]. Transportation Research Part C: Emerging Technologies, 2005, 13(3): 211. DOI:10.1016/j.trc.2005.04.007 |
| [13] |
CHEN D. Research on traffic flow prediction in the big data environment based on the improved RBF neural network[J]. IEEE Transactions on Industrial Informatics, 2017, 13(4): 2000. DOI:10.1109/TⅡ.2017.2682855 |
| [14] |
许亚琛, 吕柳璇, 黄利华, 等. 指路标志版面信息量与布局设计关系研究[J]. 公路交通科技, 2018, 35(2): 109. XU Yachen, LV Liuxuan, HUANG Lihua, et al. Study on relation between information volume and layout design of guide signs[J]. Journal of Highway and Transportation Research and Development, 2018, 35(2): 109. DOI:10.3969/j.issn.1002-0268.2018.02.015 |
| [15] |
WICKENS C D, GORDON S E, LIU Y. An introduction to human factors engineering[M]. New York: Longman, 1998. DOI:10.1136/qhc.11.4.393
|
| [16] |
ALEXANDER G J, LUNENFELD H. Positive guidance in traffic control (Office of Traffic Operations report)[R]. Washington DC: Department of Transportation, Federal Highway Administration, 1975
|
| [17] |
冯浩, 席建锋, 矫成武. 基于前视距离的路侧交通标志设置方法[J]. 吉林大学学报(工学版), 2007, 37(4): 782. FENG Hao, XI Jianfeng, JIAO Chengwu. Placement of roadside traffic signs based on visibility distance[J]. Journal of Jilin University (Engineering and Technology Edition), 2007, 37(4): 782. DOI:10.3969/j.issn.1671-5497.2007.04.010 |
| [18] |
沈强儒, 杨少伟, 赵一飞, 等. 菱形立交分流区主线线形指标分析[J]. 哈尔滨工业大学学报, 2015, 47(9): 90. SHEN Qiangru, YANG Shaowei, ZHAO Yifei, et al. Analysis on mainline alignment index in diamond interchange diverging areas[J]. Journal of Harbin Institute of Technology, 2015, 47(9): 90. DOI:10.11918/j.issn.0367-6234.2015.09.017 |
| [19] |
LIU Bohua, SUN Lishan, RONG Jian. Driver's visual cognition behaviors of traffic signs based on eye movement parameters[J]. Journal of Transportation Systems Engineering and Information Technology, 2011, 11(4): 22. DOI:10.1016/S1570-6672(10)60129-8 |
| [20] |
JAYAKRISHNAN R, MAHMASSANI H S, HU T Y. An evaluation tool for advanced traffic information and management systems in urban networks[J]. Transportation Research Part C: Emerging Technologies, 1994, 2(3): 129. DOI:10.1016/0968-090X(94)90005-1 |
| [21] |
FULLER R. Towards a general theory of driver behaviour[J]. Accident Analysis & Prevention, 2005, 37(3): 461. DOI:10.1016/j.aap.2004.11.003 |
| [22] |
CHU H C. Assessing factors causing severe injuries in crashes of high-deck buses in long-distance driving on freeways[J]. Accident Analysis & Prevention, 2014, 62: 130. DOI:10.1016/j.aap.2013.09.016 |
| [23] |
BUI K N, CAMACHO D, JUNG J E. Real-time traffic flow management based on inter-object communication: a case study at intersection[J]. Mobile Networks and Applications, 2017, 22(4): 613. DOI:10.1007/s11036-016-0800-y |
| [24] |
LAI G, CHANG W, YANG Y, et al. Modeling long-and short-term temporal patterns with deep neural networks[C]// Proceedings of the 41st International ACM SIGIR Conference on Research & Development in Information Retrieval. New York: ACM, 2018: 95. DOI: 10.1145/3209978.3210006
|
| [25] |
WU Y, TAN H, QIN L, et al. A hybrid deep learning based traffic flow prediction method and its understanding[J]. Transportation Research Part C: Emerging Technologies, 2018, 90: 166. DOI:10.1016/j.trc.2018.03.001 |
 2020, Vol. 52
2020, Vol. 52


