2. 中国电子科技集团第五十八研究所,江苏 无锡 214000
2. The 58th Research Institute of China Electronics Technology Group Corporation, Wuxi 214000, Jiangsu, China
坐标旋转数字计算机(CORDIC)算法的基本思想是运用旋转迭代等方法,采用运算基数角度不断逼近目标角度[1],只使用简单的移位和加减操作,即可计算三角函数、反三角函数和双曲函数等超越函数[2-3].该算法具有易于实现、可移植性强、精度可调等特点[4],常应用于数字频率合成、数字图形处理、机器人学、矩阵计算等领域,因而受到众多科研院校的广泛研究[5-6].
为了适应于现代数字系统的需要,开发高性能的CORDIC算法,众多学者对其提出了改进方案.文献[7]中传统的流水线型CORDIC算法虽然具有一定的精度,但所需的迭代单元级数和迭代次数较多,且需要通过上级迭代剩余角度的符号判断下级旋转迭代的方向,当输出位宽增大时,硬件资源消耗将大幅增加.文献[8]中提出的混合型CORDIC算法虽然可以快速调节旋转角度基数,但是其以较多的迭代次数来保证输出精度,且调整方程系数的电路结构复杂,存在硬件资源消耗过多的问题.文献[9]中设计的免迭代CORDIC算法采用合并迭代结构将多次迭代合并为一次迭代旋转,具有输出时延短的特点,但是运算精度却有待提高.文献[10]中基于离散傅里叶变换的并行补偿型CORDIC算法对缩放因子进行补偿计算,具有一定的输出精度,但是电路结构复杂,需要消耗额外的硬件资源用于补偿和存放缩放因子.文献[11]中提出的基于直接旋转的CORDIC算法虽然避免了缩放因子的计算,但是其只能逆时针旋转逼近输入角度,仍然具有较大的迭代运算量.
本文在文献[11]的基础上对CORDIC算法进行优化与改进,提出了双向预判免缩放因子CORDIC算法,其通过角度二进制编码后的码值即可预判每次的旋转迭代方向.此算法将输入角度分解为两个阶段处理,在第1阶段中利用查找表一步旋转到初始角度,然后在第2阶段中根据二进制编码后码值中1的个数,选择恒定顺时针或逆时针方向进行免缩放因子旋转迭代,减少了迭代单元级数和迭代次数,提高了输出精度,最后通过角度区间折叠方法将运算角度覆盖到整个圆周,确保了运算范围.
1 双向预判免缩放因子旋转 1.1 角度二进制编码对于输入角度为[0, π/4)内的角度θ0,采用n位二进制小数表示为
| $ \theta_{0}=\sum\limits_{k=1}^{n} b_{k} 2^{-k}, $ | (1) |
式中bk为0或1.将θ0前4位按位展开后为
| $ \theta_{0}=b_{1} 2^{-1}+b_{2} 2^{-2}+b_{3} 2^{-3}+b_{4} 2^{-4}+\sum\limits_{k=5}^{n} b_{k} 2^{-k}. $ | (2) |
当式(2)中bk的值为1时,则需要进行逆时针旋转2-k弧度; 当bk为0时,则不需要进行任何角度的旋转[12].经过角度编码后的旋转向量无需根据上次的迭代结果判断下次的旋转方向,避免了迭代方向的不确定性.若式(1)中k增大时,则tan(2-k)-2-k的绝对值越来越小,且当k≥n/3时,有|tan(2-k)-2-k|<2-n,因此tan(2-k)与2-k之间的误差小于n位二进制小数能够表示的精度,计算误差可以忽略不计.则可用2-k近似表示tan(2-k),只需要通过移位和加减运算即可实现,避免进行乘法运算.
1.2 建立小容量正余弦值查找表本文采用13位二进制数表示[0, π/4)内的输入角度,而[π/4, 2π)内输入角度的正弦和余弦函数值可以通过三角函数公式变换后获得,则只需要输入[0, π/4)内的角度值即可.此时n值为13,带入公式(2)可知,当k <13/3时,不可用2-k近似表示tan(2-k),否则将会引入较大的计算误差,因此建立小容量正余弦值查找表(见表 1),用以保证输出精度,且所消耗的寄存器也较少.
| 表 1 小容量正余弦值查找表 Tab. 1 Lookup table for small capacity sine and cosine values |
根据[0, π/4)内输入角度的前4位分别为0000到1101,且后9位全为0时的初始角度η,建立14个14位的正余弦值查找表,表中将cos η和sin η值的输出位宽扩展1位,用于减小计算中的截断误差.
1.3 角度区间折叠对于流水线型CORDIC算法,虽然随着迭代次数的增多,其运算范围也随之增加,但是当迭代次数趋近于无穷大时,最大运算范围接近[-1.744, 1.744]rad,而无法覆盖整个圆周[13].但正弦函数与余弦函数都具有对称性,因此可以将[0, 2π)的角度划分为8个区间,利用三角公式变换将整个圆周内的角度折叠映射到[0, π/4)内,角度区间转化如表 2所示.
| 表 2 角度区间转化 Tab. 2 Angle interval conversion |
在本文的双向预判免缩放因子型CORDIC算法的实现过程中,首先计算[0, π/4)内的正弦值和余弦值,然后比较3位角度区间编码值,最后通过角度区间折叠转换到不同的角度区间,输出相应的运算结果.3位编码值中的次高位和第3位相同与否决定了余弦值与正弦值是否需要进行交换,如果相同则无需交换,否则需要进行交换; 余弦值和正弦值是否需要翻转取反取决于编码值中的第3位,若第3位的值为0时,则无需翻转取反; 但当第3位为1时,则进行翻转取反输出; 若最高位的值为0,则正弦值输出为正值,否则为负值; 当最高位与次高位不同时,则余弦值输出为负值,反之为正值.采用角度区间折叠技术,保证了运算范围,同时减少了查找表所需要存储的正余弦值的个数.
1.4 双向免缩放因子旋转下面首先介绍免缩放因子旋转的基本原理.在流水线型CORDIC算法中,将正弦和余弦函数用泰勒级数展开式表示可得
| $ \begin{array}{l} \sin \theta_{0}=\theta_{0}-\frac{\theta_{0}^{3}}{6}+\frac{\theta_{0}^{5}}{120}-\cdots, \end{array} $ | (3) |
| $ \cos \theta_{0}=1-\frac{\theta_{0}^{2}}{2}+\frac{\theta_{0}^{4}}{24}-\cdots. $ | (4) |
令式(3)和(4)中的θ0=2-i,则sin θ0中的三次项可以表示为
| $ \frac{\theta_{0}^{3}}{6}=\frac{2^{-3 i}}{6}=2^{-\left(3 i+\log _{2} 6\right)}=2^{-(3 i+2.59)}. $ | (5) |
当正弦函数和余弦函数的输出位宽设定为N位,且最高位为符号位时,则式(5)中i的最大值为N-1.若3i+2.59≥N-1,可得i的取值范围为
| $ \frac{N-3.59}{3} \leqslant i \leqslant N-1, i \in N^{*}. $ | (6) |
当i的取值在式(6)范围之内时,则θ03及其更高阶的函数均已无法用L-1位二进数表示,此时可以直接取cos θ0值为1进行计算[14].
单向免缩放因子旋转可以省略缩放因子的计算,且迭代方向与角度二进制编码后的位值相对应,避免了流水线型需要不断顺时针和逆时针旋转修正角度的问题,同时也不会因为去掉了缩放因子而影响输出精度[15].然而当角度二进制编码后码值中相应位为0时,虽然不需要进行旋转迭代,但是并不能保证下一个码值在此位的值还是为0,且只能进行恒定逆时针免缩放因子旋转,所以需要消耗一个时钟周期进行此位的旋转判断,无法跳跃此位为0时的旋转判断,需要较多的迭代单元级数和次数以保证输出精度.但本文设计的CORDIC算法既可以恒定逆时针或顺时针免缩放因子旋转,也可以跳跃不需要旋转的角度,减少电路的迭代次数,提高了运算精度,其双向旋转示意见图 1.

|
图 1 双向旋转示意 Fig. 1 Schematic diagram of bidirectional rotation |
在上图中,根据表 1中设立的14个初始角度值将[0, 13/16)弧度范围内的角度均分为13等份,每一份弧度都为1/16.当由初始角度η0逆时针旋转到目标角度ηθ时,则ηθ可以表示为
| $ \eta_{\theta}=\eta_{0}+b_{5}\left(\frac{1}{2}\right)^{5}+b_{6}\left(\frac{1}{2}\right)^{6}+\cdots+b_{13}\left(\frac{1}{2}\right)^{13}. $ |
令
| $ \begin{aligned} \eta_{k}=&\left(b_{5}-1\right)\left(\frac{1}{2}\right)^{5}+\cdots+\\ &\left(b_{13}-1\right)\left(\frac{1}{2}\right)^{13}-\left(\frac{1}{2}\right)^{13}. \end{aligned} $ |
则由η0和η1旋转到目标角度的迭代次数分别为
| $ \begin{array}{c} \lambda_{0}=b_{5}+b_{6}+\cdots+b_{13} , \end{array} $ | (7) |
| $ \lambda_{1}=10-\left(b_{5}+b_{6}+\cdots+b_{13}\right)=10-\lambda_{0}. $ | (8) |
通过式(7)和(8)可知,当λ0≥λ1时,则λ0≥10-λ0,得λ0≥5,因此当输入角度二进制编码后码值中1的个数≥5时,此时用η1旋转迭代的次数比η0少; 当λ0<λ1时,则λ0<10-λ0,得λ0 < 5,若二进制编码后码值中1的个数<5时,此时用η0旋转迭代的次数比η1少.因此与单向免缩放因子型和流水线型CORDIC算法相比,迭代单元的级数分别减少了4级和8级,降低了电路的硬件资源消耗.采用13位二进制小数表示π/4 rad可为1100100011110,对于图 1中0000到1100这12个分区和1100到π/4区间而言,根据相应的迭代次数对应的种类,单向免缩放因子型CORDIC算法在初始角度η0的基础上进行恒定逆时针旋转时,由排列组合相关知识可得每个分区间的迭代次数Ld和总迭代次数Nunid分别为:
| $ \begin{array}{c} L_{d}=\sum\limits_{j=1}^{m} j \mathrm{C}_{m}^{j}=m \times 2^{m-1}, d=1, \cdots, 12 ;\\ L_{13}=m \mathrm{C}_{m}^{3}-4 m^{2}+31 m-49+ \\ \sum\limits_{r=5}^{m-3} r\left[\mathrm{C}_{m-1}^{r}+\mathrm{C}_{m-4}^{r-1}-\mathrm{C}_{m-8}^{r-5}\right]; \\ N_{\mathrm{unid}}=\sum\limits_{c=1}^{13} L_{c}, c=1, \cdots, 13. \end{array} $ |
上式中,m为建立4位查找表后剩余的二进制编码的位数,其值为n-4.当根据码值中1的个数合理选择η0和η1进行双向预判免缩放因子旋转迭代时,对m进行分奇偶数讨论后,可得在单向免缩放因子型基础上减少的总迭代次数为
| $ \begin{aligned} N_{\text {dec_sum }}=& \sum\limits_{t=t_{0}}^{m-1} t \mathrm{C}_{m}^{\frac{m+1}{2}+\frac{1}{2}} \times 12+\sum\limits_{h=t_{0}}^{m-7} h\left[\mathrm{C}_{m-1}^{\frac{m+1}{2}+\frac{h}{2}}+\right.\\ &\left.\mathrm{C}_{m-4}^{\frac{m-1}{2}+\frac{h}{2}}-\mathrm{C}_{m-8}^{\frac{m+1}{2}+\frac{h}{2}-5}\right]+m^{2}-5 m+2. \end{aligned} $ |
| $ \left\{\begin{array}{c} t=2 k, t_{0}=2, h=2 l, 1 \leqslant l \leqslant \frac{m-7}{2}, \\ 1 \leqslant k \leqslant \frac{m-1}{2}, m \text { 为奇数 }; \\ t=2 k-1, h=2 l-1, t_{0}=1, 1 \leqslant k \leqslant \frac{m}{2} , \\ 1 \leqslant l \leqslant \frac{m-6}{2}, m \text { 为偶数. } \end{array}\right. $ |
对于最高位为符号位的N位流水线型CORDIC算法,其总迭代次数为
| $ N_{\text {pipel }}=(N-1) \times 2^{(N-1)}. $ |
相比于单向免缩放因子型和流水线型CORDIC算法的总迭代次数,其降低率分别为
| $ \begin{array}{c} I_{\text {dec_pipel }}=\frac{N_{\text {dec_sum }}}{N_{\text {unid }}} \times 100 \% \\ I_{\text {dec_unid }}=\frac{N_{\text {pipel }}-\left(N_{\text {unid }}-N_{\text {dec_sum }}\right)}{N_{\text {pipel }}} \times 100 \% . \end{array} $ |
将m=9和N=14代入上式计算后可得,总迭代次数降低率分别为15.9%和76.8%.总迭代次数的降低减少了旋转迭代运算过程中误差的累积,提高了算法的输出精度.
2 算法实现本文提出的双向预判免缩放因子CORDIC算法的整体结构框图见图 2.根据结构框图,在MATLAB工具上进行算法建模与仿真,并与单向免缩放因子型和流水线型CORDIC算法进行精度对比与分析,同时采用Verilog HDL硬件描述语言对各模块以及整体电路进行自顶向下的RTL级设计,最后在Xilinx公司的XC7X200t-3fbg484型号FPGA上进行电路实现,比较分析3种算法的硬件资源消耗等性能参数.
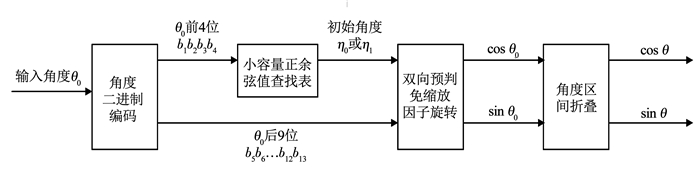
|
图 2 新型CORDIC算法整体结构框图 Fig. 2 Block diagram of CORDIC algorithm |
在相同的14位输出位宽的情况下,使用MATLAB软件对3种算法建模分析.输入角度以2-13的分辨率遍历第一象限,并且与标准正余弦函数分别相减后得到其绝对误差,同时在绝对误差图中标识最大值点和最小值点,然后将取绝对值后的绝对误差进行算术平均以获得平均误差,最后采用相应的函数分别计算出标准差与方差,比较分析3种算法的输出精度.第一象限内3种算法的余弦函数绝对误差结果如图 3所示,其精度对比见表 3,并进行了精度对比分析.
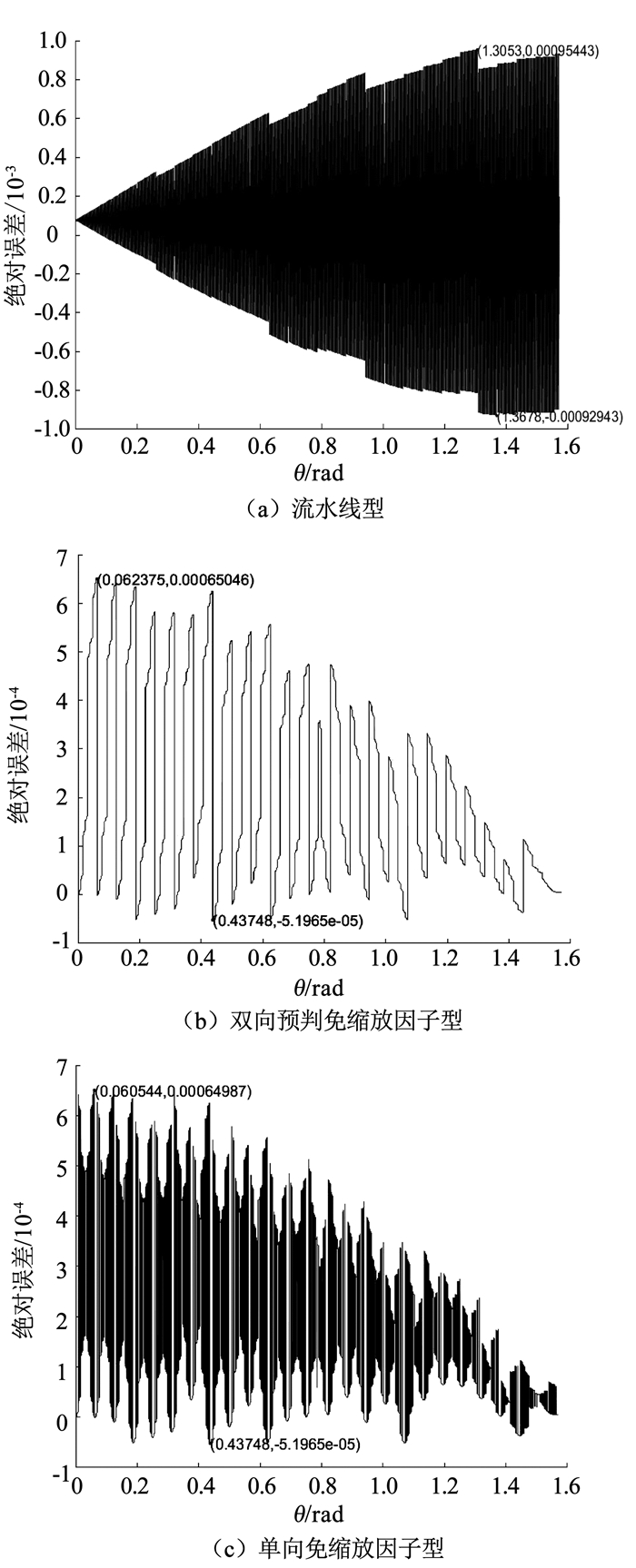
|
图 3 3种算法余弦函数的绝对误差 Fig. 3 Absolute errors of cosine function of three algorithms |
| 表 3 3种算法余弦函数的精度对比 Tab. 3 Accuracy comparison of cosine function of three algorithms |
通过图 3与表 3可以看出,与流水线型和单向免缩放因子型相比,本文提出的CORDIC算法的平均误差分别降低了47.5%和18.8%,绝对误差的最大值以及取绝对值后绝对误差的方差和标准差都具有一定的降低,提高了算法的输出精度.主要原因在于即使流水线型CORDIC算法中的旋转向量旋转到了目标角度,但如果未完成13次迭代,则还需要顺时针或者逆时针旋转不同角度,直到完成13次迭代,因此输出误差较大.单向免缩放因子型CORDIC算法虽然避免了不必要的旋转迭代,但是其迭代次数还是较多,运算过程中产生的累积误差较大.而改进算法能够根据角度二进制编码后码值中1的个数,在准确的初始角度的正余弦值基础上,进行恒定顺时针或逆时针免缩放因子旋转迭代,减少了总迭代次数,降低了运算过程中误差的累积,提高了算法的输出精度.
在相同的时序、面积和电路环境属性等约束条件下,使用Vivado软件对3种算法进行综合,对寄存器消耗量、查找表消耗量等硬件资源消耗参数,以及最大输出时延进行对比分析,逻辑综合结果如表 4所示.同时,在表 5中列出了本文提出的双向预判免缩放因子型CORDIC算法与近年来国内外部分CORDIC算法文献的精度对比.
| 表 4 三种算法的逻辑综合结果 Tab. 4 Logical synthesis results of three algorithms |
从表 4中可以看出本文提出的CORDIC算法相比于流水线型和单向免缩放因子型CORDIC算法,硬件资源消耗具有一定的下降.虽然本文的算法增设了双向预判选择单元,消耗了少量的寄存器和查找表,但是迭代单元级数由流水线型的13级和单向免缩放因子旋转型的9级缩减到了5级,使硬件资源消耗有所下降.从表 5中可知,与文献[9-11]相比,CORDIC算法的平均误差分别降低了7.8%、15.5%、57.2%,同时在绝对误差的最大值和最大输出延时方面也都具有较大幅度的降低.
| 表 5 CORDIC算法的精度对比 Tab. 5 Accuracy comparison of CORDIC algorithms |
针对流水线型CORDIC算法的运算精度低、输出时延长等问题,本文结合角度二进制编码和角度区间折叠等手段,建立了小容量正余弦值查找表,提出并实现了双向免缩放因子CORDIC算法.提出的CORDIC算法对于某一输入目标角度,根据角度二进制编码后码值中1的个数,选择初始角度并预判迭代旋转方向,避免了每次旋转迭代方向的不确定性,减少了迭代单元级数和迭代次数,最短在两个时钟周期内即可输出运算结果.在相同的14位位宽的情况下,对比流水线型和单向免缩放因子型CORDIC算法的运算精度,则分别提高了47.5%、18.8%,最大输出时延分别降低了53.8%、40.0%,算法实现电路的寄存器和查找表的消耗量也有所下降,接下来还可以采用格雷码对角度区间码值进行编码,降低相邻状态转换时出错的可能性.本文设计的CORDIC算法在输出精度与输出时延等方面具有显著的优势,适用于实时性强、高精度、低功耗的现代数字通信系统.
| [1] |
HOANG T T, LE D H, PHAM C K. Minimum adder-delay architecture of 8/16/32-point DCT based on fixed-rotation adaptive CORDIC[J]. IEICE Electronics Express, 2018, 15(10): 20180302. DOI:10.1587/elex.15.20180302 |
| [2] |
姚亚峰, 邹凌志, 王巍, 等. 低消耗免查找表CORDIC算法[J]. 哈尔滨工业大学学报, 2017, 49(11): 109. YAO Yafeng, ZOU Lingzhi, WANG Wei, et al. Low-consumption and LUT-omitted CORDIC algorithm[J]. Journal of Harbin Institute of Technology, 2017, 49(11): 109. DOI:10.11918/j.issn.0367-6234.201704019 |
| [3] |
NGUYEN H T, HGUYEN X T, PHAM C K. A low power hybrid adaptive CORDIC[J]. IEEE Transactions on Circuits and Systems, 2018, 65(4): 496. |
| [4] |
RAMADOSS R, KERMANI M M, AZARDERAKHSH R. Reliable hardware architectures of the CORDIC algorithm with a fixed angle of rotations[J]. IEEE Transactions on Circuits and System Ⅱ: Express Briefs, 2017, 64(8): 972. DOI:10.1109/TCSII.2016.2624508 |
| [5] |
王国洪, 宛强, 姚亚峰, 等. 精确频率输出的超低时延DDS电路设计[J]. 哈尔滨工业大学学报, 2019, 51(5): 44. WANG Guohong, WAN Qiang, YAO Yafeng, et al. A DDS circuit design with ultra-low latency and exact output frenquency[J]. Journal of Harbin Institute of Technology, 2019, 51(5): 44. DOI:10.11918/j.issn.0367-6234.201805108 |
| [6] |
AGGARWAL S, MEHER P K, KHARE K. Concept, design, and implementation of reconfigurable CORDIC[J]. IEEE Transactions on Very Large Scale Integration (VLSI) Systems, 2016, 24(4): 1588. DOI:10.1109/TVLSI.2015.2445855 |
| [7] |
HUANG Hai, XIAO Liyi. CORDIC based fast radix-2 DCT algorithm[J]. IEEE Signal Processing Letters, 2013, 20(5): 483. DOI:10.1109/LSP.2013.2252616 |
| [8] |
SHUKLA R, RAY K C. Low latency hybrid CORDIC algorithm[J]. IEEE Transactions on Computers, 2014, 63(12): 3066. DOI:10.1109/TC.2013.173 |
| [9] |
YAO Yafeng, FENG Zhongxiu. BBR-based iteration-free CORDIC algorithm[J]. Journal of Circuits Systems and Computers, 2018, 27(5): 101. |
| [10] |
KULSHRESHTHA T, DHAR A. CORDIC-based Hann windowed sliding DFT architecture for real-time spectrum analysis with bounded error-accumulation[J]. IET Circuits, Devices & Systems, 2017, 11(5): 487. |
| [11] |
姚亚峰, 冯中秀, 陈朝. 直接旋转CORDIC算法及其高效实现[J]. 华中科技大学学报(自然科学版), 2016, 44(10): 113. YAO Yafeng, FENG Zhongxiu, CHEN Zhao. Direct rotation CORDIC algorithm and its implementation[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2016, 44(10): 113. DOI:10.13245/j.hust.161022 |
| [12] |
PRASAD N, TRIPATHY M R, DAS A D, et al. Efficient VLSI implementation of CORDIC based direct digital synthesizer[C]// Intelligent Computing, Communication and Devices. New Delhi: Springer, 2015, 308: 597
|
| [13] |
KAMBO H M A D, KHAN S A. IS-CORDIC: a fixed-point ecoded ingle teration CORDIC rchitecture[J]. International Journal of Electronics, 2014, 101(6): 789. DOI:10.1080/00207217.2013.803432 |
| [14] |
AGUIRRE-RAMOS F, MORALES-REYES A, CUMPLIDO R, et al. An area efficient composed CORDIC architecture[J]. Advances in Electrical and Computer Engineering, 2014, 14(2): 113. DOI:10.4316/AECE.2014.02019 |
| [15] |
MEHER P K, PARK S Y. CORDIC designs for fixed angle of rotation[J]. IEEE Transactions on Very Large Scale Integration Systems, 2013, 21(2): 217. DOI:10.1109/TVLSI.2012.2187080 |
 2021, Vol. 53
2021, Vol. 53


