2. 省部共建西部绿色建筑国家重点实验室(西安建筑科技大学),西安 710055
2. State Key Lab of Green Building in Western China (Xi'an University of Architecture and Technology), Xi'an 710055, China
水泥基灌浆料具有流动性好(可不振捣)、微膨胀、早期强度发展快(3 d强度即可达到40 MPa以上)、强度高(>60 MPa)的特点,早期主要用于地脚螺栓锚固、设备基础的二次灌浆和桥梁、堤坝的抢险工程中,近年来被广泛应用于钢筋混凝土结构加固改造中[1-2]。
随着水泥基灌浆料在工程中的广泛应用,国内外学者对水泥基灌浆料的相关性能进行了研究,取得了一定的研究成果。目前对水泥基灌浆料的研究主要集中在基本力学性能方面[3-7],部分学者针对钢筋与水泥基灌浆料黏结性能[8-10]、水泥基灌浆料与混凝土界面性能[11]、水泥基灌浆料加固钢筋混凝土构件承载性能[12-13]也展开了初步研究,而对水泥基灌浆料受压应力-应变关系的研究却鲜有报道[14]。作为结构构件承载性能分析的基础,水泥基灌浆料受压本构模型的缺失一定程度阻碍了其在钢筋混凝土结构加固工程中的应用。此外,加固后结构构件的承载性能具有明显的时变特征,使用具有早期强度增长快特点的水泥基灌浆料对既有钢筋混凝土结构进行加固,评估加固后结构的承载性能,可以在确保结构安全的前提下缩短现场湿作业时间、加快施工进度。因此,深入研究早龄期水泥基灌浆料的基本力学性能和受压应力-应变关系,可为加固后构件的承载性能评估和安全性分析提供可靠的理论基础。
基于此,本文考虑不同龄期(1 d、2 d、3 d、7 d和28 d),对15个水泥基灌浆料试件和15个同强度混凝土试件开展单轴受压全过程试验,分析龄期对水泥基灌浆料、同强度混凝土试件受压应力-应变曲线特征参数的影响,并将水泥基灌浆料试件试验结果与同强度混凝土进行对比。结合现有研究和水泥基灌浆料自身特点,考虑龄期建立水泥基灌浆料单轴受压本构模型。
1 试验概述 1.1 试验原材料本文中所采用的水泥基灌浆料为北京中德新亚建筑技术有限公司生产的CGM-270高强无收缩加固型水泥基灌浆料,见图 1,其主要成分包括P·O 32.5水泥、石粒骨料、膨胀剂和减水剂,石粒骨料的最大粒径为4.75~16 mm。参考GB/T 50448—2015《水泥基灌浆材料应用技术规范》[15],对水泥基灌浆料的流动度、竖向膨胀率和抗压强度等主要性能指标进行检验,测试结果见表 1,本文采用的水泥基灌浆料性能符合规范要求。

|
图 1 CGM-270高强无收缩灌浆料 Fig. 1 CGM-270 high-strength non-shrinkage cementitious grout |
| 表 1 水泥基灌浆料主要性能指标 Tab. 1 Performance indexes of cementitious grout |
将水泥基灌浆料与自来水按100∶9.5的比例拌合均匀后浇入尺寸为100 mm×100 mm×100 mm和100 mm×100 mm×300 mm的塑料模具中制作立方体和棱柱体试件。浇筑好的试件在标准养护室(温度20±3 ℃,相对湿度≥90%)中养护24 h后拆模,拆模后在自然环境中洒水覆膜养护至试验龄期,每个试验龄期条件下各制作3个试件。
采用立方体抗压强度与水泥基灌浆料接近的普通混凝土作为对照组试件,配合比见表 2。水泥:普通硅酸盐水泥(P·O 42.5);粗骨料:5~25 mm连续级配的花岗岩碎石,表观密度为2 700 kg/m3;细骨料:西安市沣河河砂,细度模数为2.85,堆积密度为1 550 kg/m3;减水剂:聚羧酸系高性能减水剂。根据GB/T 50081—2019《混凝土物理力学性能试验方法标准》[16],按表 2配合比制作尺寸、数量与水泥基灌浆料相同的试件,成型后与水泥基灌浆料同条件养护至试验龄期。
| 表 2 混凝土配合比 Tab. 2 Mix proportions of concrete |
采用3 000 kN万能液压试验机进行单轴受压试验,见图 2。

|
图 2 单轴受压试验加载装置(mm) Fig. 2 Test equipment for uniaxial compression test (mm) |
采用位移控制加载,加载速率为0.2 mm/min,加载过程中用自制的铝支架固定位移计,测量试件两侧200 mm标距范围内的压缩变形值。试验过程中试件的轴向荷载、纵向变形数据均由TDS-602数据采集仪采集。
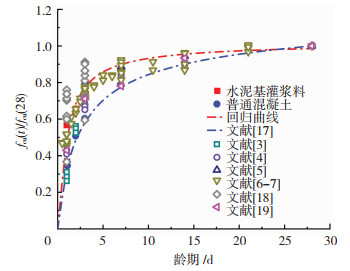
2 试验结果与分析 2.1 立方体抗压强度从图 3试件立方体抗压强度fcu随龄期的变化规律可看出:随着龄期增大,各试件均表现为前7 d强度增长迅速,7 d后增长速度逐渐放缓并逐渐趋于稳定;与同强度混凝土相比,水泥基灌浆料试件具有明显的早期强度发展快的特点。对同强度混凝土而言,其1 d、7 d抗压强度分别为28 d抗压强度的34.1%和60.2%;而对水泥基灌浆料而言,其1 d抗压强度和7 d抗压强度分别达到了28 d抗压强度的56.7%和77.4%。参考文献[17]对试验数据进行回归分析,得到水泥基灌浆料立方体抗压强度的预测公式,见式(1)。将模型计算结果与本文和文献[3-7, 18-19]试验数据进行对比,计算结果与试验结果基本吻合,建议模型可用于早龄期水泥基灌浆料立方体抗压强度的计算。
| $ \begin{array}{c} {f_{{\rm{cu}}}}(t) = {f_{{\rm{cu}}}}(28) \times \left( {\frac{t}{{0.906 + 0.982t}}} \right)\\ {R^2} = 0.967,1\ {\rm{d}} \le t \le 28\ {\rm{d}} \end{array} $ | (1) |
|
图 3 立方体抗压强度与龄期的关系 Fig. 3 Relationship between cubic compressive strength and age |
对龄期为1 d、2 d的试件,加载时首先在试件棱角处出现裂缝,随着加载的进行,裂缝宽度逐渐增大,并向上下延伸,棱角裂缝贯通后试件发生破坏,表现出一定的塑性破坏特点;对龄期3 d及以上的试件,加载时首先在试件侧表面中间区域出现竖向裂缝,随着加载的进行,裂缝不断延伸、发展,裂缝宽度增大,主裂缝逐渐贯通,破坏时有碎片崩出,并伴有较大的崩裂声,破坏以脆性破坏为主。与同强度混凝土相比,水泥基灌浆料棱柱体试件加载时裂缝发展阶段持续时间较短,达到峰值荷载以后水泥基灌浆料棱柱体试件更易发生崩裂,试件迅速丧失承载力,试件破坏后的整体性较差,见图 4。对比试件破坏面可以发现,水泥基灌浆料试件在破坏时,穿越破坏面的部分骨料被劈开,破坏截面平整、光滑,这与同强度混凝土的破坏情况存在显著区别。

|
图 4 试件破坏形态 Fig. 4 Failure modes of specimens |
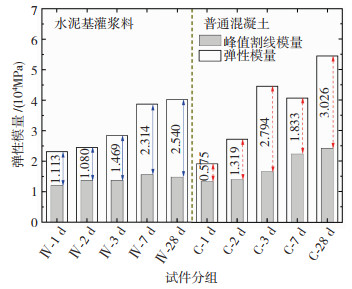
图 5给出了各试件的受压应力-应变全曲线(图中Ⅳ和C分别表示水泥基灌浆料和同强度的混凝土,1 d表示试件龄期为1 d,下同),从图 5可看出:随着龄期的增长,水泥基灌浆料和同强度混凝土试件单轴受压应力-应变曲线上升段斜率均有不同程度的增加,线弹性变形阶段延长,试件弹性模量和峰值割线模量的差值逐渐变大(图 6),峰值应变逐渐增大,但曲线下降段逐渐变陡,极限应变和峰值应变的差值逐渐变小(图 7),试件逐渐表现出显著的脆性特征。与同强度混凝土相比,水泥基灌浆料试件峰值应力较大,尤其是对于龄期在3 d及以前的试件,两类试件在峰值应力上的差值更为明显,这与水泥基灌浆料早期强度发展快的特点一致。

|
图 5 受压应力-应变曲线 Fig. 5 Compressive stress-strain curves |
|
图 6 峰值割线模量与弹性模量差值 Fig. 6 Differences between peak secant modulus and elastic modulus |

|
图 7 极限应变与峰值应变差值 Fig. 7 Differences between ultimate strain and peak strain |
1) 峰值应力σ1。图 8给出了各试件轴心抗压强度与立方体抗压强度的关系,从图 8可看出:各试件轴心抗压强度随龄期的变化趋势与立方体抗压强度基本一致,其中水泥基灌浆料轴心抗压强度与立方体抗压强度的强度比为0.900~0.990,显著高于同强度混凝土的强度比(约0.756~0.921);与同强度混凝土相比,水泥基灌浆料立方体抗压强度、轴心抗压强度随龄期的变化曲线斜率较大,也说明水泥基灌浆料早期强度发展较快。参考文献[20]对水泥基灌浆料轴心抗压强度与立方体抗压强度数据进行回归分析(图 9),得到强度换算关系:
| $ \sigma_1=0.916 f_{\mathrm{cu}}, R^2=0.988 $ | (2) |

|
图 8 轴心抗压强度与立方体抗压强度比值 Fig. 8 Ratio of axial compressive strength to cubic compressive strength |

|
图 9 峰值应力与立方体抗压强度关系 Fig. 9 Relationship between peak stress and cubic compressive strength |
本文基于试验数据得到的水泥基灌浆料轴心抗压强度与立方体抗压强度间的换算系数0.916与文献[3]给出的系数0.920和文献[4]给出的系数0.910接近,明显大于同强度混凝土轴心抗压强度与立方体抗压强度换算系数(0.832),但仍在换算系数范围0.700~0.920内[20]。
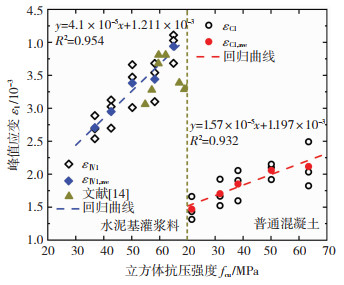
2) 峰值应变ε1。水泥基灌浆料试件的峰值应变明显大于同强度混凝土,这是因为试件变形主要由粗骨料变形、水泥浆体变形及微裂缝的形成和扩展三部分组成。在试件应力达到峰值点前,试件内部微裂缝处于稳定发展阶段,试件的变形主要取决于试件内粗骨料的变形。同强度混凝土试件粗骨料粒径较大,加载过程中粗骨料变形较小。因此,已有混凝土峰值应变的计算公式不适用于水泥基灌浆料。对试验数据进行回归分析,见图 10,得到水泥基灌浆料峰值应变计算公式:
| $ \varepsilon_1=4.1 \times 10^{-5} f_{\mathrm{cu}}+1.211 \times 10^{-3}, R^2=0.954 $ | (3) |
|
图 10 峰值应变与立方体抗压强度关系 Fig. 10 Relationship between peak strain and cubic compressive strength |
对比公式计算结果和文献[14]试验数据可看出,文献[14]试验数据相对离散,但基本分布在计算曲线两侧,试验数据变化趋势与计算曲线符合良好,说明建议公式能相对准确地计算水泥基灌浆料的峰值应变。
3) 弹性模量Ec。弹性模量定义为应力-应变曲线上升段从原点至40%峰值应力点对应的割线模量。随龄期的增大,水泥基灌浆料试件的弹性模量整体呈现持续增长的趋势;水泥基灌浆料的弹性模量明显小于同强度混凝土,与文献[4, 14]给出的结论一致。这是因为试件的弹性模量主要取决于骨料的弹性模量,混凝土中含有的粗骨料的弹性模量较大,进而导致试件具有较大的弹性模量。参考文献[21]对试验数据进行回归分析,见图 11,得到水泥基灌浆料弹性模量的计算公式:
| $ E_{\mathrm{c}}=9575.5 \sqrt{f_{\mathrm{cu}}}-36722, R^2=0.930 $ | (4) |

|
图 11 弹性模量与立方体抗压强度关系 Fig. 11 Relationship between elastic modulus and cubic compressive strength |
4) 应变延性系数β。为了定量分析水泥基灌浆料的受力变形性能,定义极限应变与初始屈服应变的比值为试件的应变延性系数,见式(5)。采用能量等值法来确定初始屈服点[22],见图 12。
| $ \beta=\frac{\varepsilon_u}{\varepsilon_y} $ | (5) |

|
图 12 应变延性系数计算简图 Fig. 12 Calculation diagram of strain ductility coefficient |
式中εu为试件的极限应变,εy为试件初始屈服点对应的应变。
从图 13试件的应变延性系数可看出:随龄期的增大,水泥基灌浆料、同强度混凝土试件应变延性系数整体上均有不同程度的增大;水泥基灌浆料试件应变延性系数整体上较同强度混凝土试件大,这是因为尽管水泥基灌浆料受压应力-应变曲线下降段的斜率较同强度混凝土大,但水泥基灌浆料峰值应变、极限应变明显大于同强度混凝土。

|
图 13 试件应变延性系数 Fig. 13 Strain ductility coefficient of specimens |
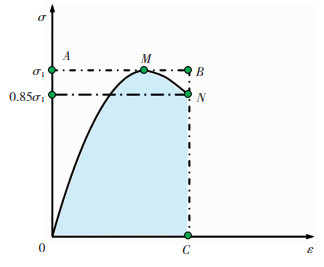
5) 能量耗散系数ηe。引入能量耗散系数来对试件受力过程中的耗能情况进行研究[22],计算简图见图 14,其计算公式:
| $ \eta_{\mathrm{e}}=\frac{S_{0 M N C}}{S_{0 A B C}} $ | (6) |
|
图 14 能量耗散系数计算简图 Fig. 14 Calculation diagram of energy dissipation coefficient |
式中:S0MNC为应力-应变曲线经峰值点至下降段0.85倍峰值应力与坐标轴所围成的面积,S0ABC为过峰值点至下降段0.85倍峰值应力对应同一应变矩形的面积。
图 15给出了各试件能量耗散系数,从图 15可看出:随着龄期的增大,各试件能量耗散系数整体呈增大趋势,但增大幅度较小(最大增幅分别为3.1%和5.5%);水泥基灌浆料能量耗散系数较同强度混凝土大,这是因为同龄期下水泥基灌浆料峰值应力、峰值应变和极限应变均较同强度混凝土大,水泥基灌浆料受压应力-应变曲线与坐标轴所围成的面积较大。

|
图 15 试件能量耗散系数 Fig. 15 Energy dissipation coefficient of specimens |
目前,国内外学者基于混凝土试验结果提出了多种单轴受压本构模型[23-26],但关于水泥基灌浆料单轴受压性能的研究相对欠缺,考虑水泥基灌浆料龄期的单轴受压本构模型尚未提出。既有基于混凝土单轴受压本构模型难以准确描述水泥基灌浆料的变形特征,计算结果存在一定安全隐患。因此,本文采用已有单轴受压本构模型,包括过镇海模型[23]、Carreira模型[24]、Wee模型[25]和GB 50010—2010《混凝土结构设计规范》建议模型[26],对本文试验数据进行回归分析,并与试验曲线进行对比(图 16)。由图 16可见:对曲线上升段而言,各模型曲线与试验曲线偏差较小,其中,规范建议模型曲线与试验曲线吻合效果最好;对曲线下降段而言,不同模型拟合结果的吻合程度差异较大,其中Carreira模型、Wee模型高估了水泥基灌浆料试件在受压达到峰值点后的延性,而过镇海模型、规范建议模型对试件在受压峰值点后的延性有一定程度的低估。基于对比结果,结合水泥基灌浆料自身特点,对已有模型参数进行修正,建立了适用于水泥基灌浆料的修正的分段式受压本构模型,上升段采用规范建议模型,下降段采用Wee模型。

|
图 16 各模型曲线与试验曲线对比 Fig. 16 Comparison between theoretical and test curves |
1) 上升段
| $ \begin{array}{c} \sigma = \left( {\frac{{n{\rho _{\rm{c}}}}}{{n - 1 + {x^n}}}} \right){E_{\rm{c}}}\varepsilon \\ 其中{\rho _{\rm{c}}} = \frac{{{\sigma _1}}}{{{E_{\rm{c}}}{\varepsilon _1}}}, n = \frac{{{E_{\rm{c}}}{\varepsilon _1}}}{{{E_{\rm{c}}}{\varepsilon _1} - {\sigma _1}}} \end{array} $ | (7) |
2) 下降段
| $ \begin{array}{c} y = \frac{{{k_1}\gamma x}}{{{k_1}\gamma - 1 + {x^{{k_2}\gamma }}}}\\ 其中\gamma = \frac{1}{{1 - {\sigma _1}/\left( {{\varepsilon _1}{E_c}} \right)}} \end{array} $ | (8) |
式中:x=ε/ε1,y=σ/σ1,峰值应力σ1和峰值应变ε1分别按式(2)、(3)计算,弹性模量Ec按式(4)计算。结合本文试验数据,修正模型中各参数可通过计算或回归分析得到,见表 3。
| 表 3 修正模型参数汇总 Tab. 3 Summary of parameters of modified model |
从图 16修正模型计算曲线和试验曲线的对比可看出,修正模型计算曲线与试验曲线吻合较好,本文建议的修正模型可以较为准确地描述早龄期水泥基灌浆料单轴受压作用下的变形特征。
3.2 统计损伤本构模型由损伤力学理论,在荷载作用下,水泥基灌浆料试件内的损伤逐渐积累,有效承载面积逐渐减小,试件的名义应力和有效应力满足关系[27]:
| $ \sigma =F / A $ | (9) |
| $ \sigma^* =F / A^* $ | (10) |
| $ \sigma =\frac{A^*}{A} \sigma^* $ | (11) |
式中:σ和σ*分别为试件的名义应力和有效应力,F为作用在试件上的荷载,A和A*分别为试件的名义承载面积和有效承载面积。
采用损伤变量对试件内部损伤的发展情况进行表征。损伤变量定义为试件内部损伤面积与名义承载面积的比值[28-29]:
| $ D=\frac{A-A^*}{A}=1-\frac{A^*}{A} $ | (12) |
式中:D为试件的损伤变量,0≤D≤1,D=0表示试件内部无损伤,D=1表示试件完全损坏。
由式(11)、(12)可得
| $ \sigma=(1-D) \sigma^* $ | (13) |
由应变协调原则,试件内部损伤部分应变与未损伤部分的应变一致[30]。假设试件内未损伤部分满足弹性变形规律,故式(13)可转化为
| $ \sigma=(1-D) E_{\mathrm{c}} \varepsilon $ | (14) |
当试件应变小于峰值应变(ε<ε1)时,损伤变量D与应变ε间的关系可用Weibull分布来描述[31]:
| $ \frac{\mathrm{d} D}{\mathrm{~d} \varepsilon}=\frac{p}{q}\left(\frac{\varepsilon}{q}\right)^{p-1} \exp \left[-\left(\frac{\varepsilon}{q}\right)^p\right] $ | (15) |
式中p、q分别为Weibull分布的形状参数和尺度参数,且二者均大于0。
由式(15)可得
| $ D=1-\exp \left[-\left(\frac{\varepsilon}{q}\right)^p\right] $ | (16) |
由式(14)、(16)可得
| $ \sigma=E_{\mathrm{c}} \varepsilon \exp \left[-\left(\frac{\varepsilon}{q}\right)^p\right], \varepsilon<\varepsilon_1 $ | (17) |
根据试件峰值荷载前(ε<ε1)受压应力-应变关系曲线上的几何条件:1)ε=0,σ=0;2)ε=0,dσ/dε=Ec;3)ε=ε1,σ=σ1;4)ε=ε1,dσ/dε=0,可得参数p、q表达式[31]:
| $ p=\frac{1}{\ln \left(E_{\mathrm{c}} \varepsilon_1 / \sigma_1\right)}, q=\frac{\varepsilon_1}{(1 / p)^{1 / p}} $ | (18) |
当试件应变大于峰值应变(ε≥ε1)时,可采用对数正态分布来对试件应力-应变关系进行描述[32]:
| $ \sigma=a \exp \left[-0.5\left(\frac{\ln (\varepsilon / b)}{c}\right)^2\right] $ | (19) |
上式中参数a、b分别为试件的峰值应力σ1和峰值应变ε1,因此式(19)可转化为
| $ \sigma=\sigma_1 \exp \left[-0.5\left(\frac{\ln \left(\varepsilon / \varepsilon_1\right)}{c}\right)^2\right], \varepsilon \geqslant \varepsilon_1 $ | (20) |
由式(17)、(20)可得试件统计损伤本构模型的最终表达式:
| $ \sigma = \left\{ {\begin{array}{*{20}{l}} {{E_{\rm{c}}}\varepsilon \exp \left[ { - {{\left( {\frac{\varepsilon }{q}} \right)}^p}} \right], }&{\varepsilon < {\varepsilon _1}}\\ {{\sigma _1}\exp \left[ { - 0.5{{\left( {\frac{{\ln \left( {\varepsilon /{\varepsilon _1}} \right)}}{c}} \right)}^2}} \right], }&{\varepsilon \ge {\varepsilon _1}} \end{array}} \right. $ | (21) |
由式(14), 试件损伤变量D可表示为
| $ D = \left\{ {\begin{array}{*{20}{l}} {1 - \exp \left[ { - {{\left( {\frac{\varepsilon }{q}} \right)}^p}} \right], }&{\varepsilon < {\varepsilon _1}}\\ {1 - \frac{{{\sigma _1}}}{{{E_{\rm{c}}}\varepsilon }}\exp \left[ { - 0.5{{\left( {\frac{{\ln \left( {\varepsilon /{\varepsilon _1}} \right)}}{c}} \right)}^2}} \right], }&{\varepsilon \ge {\varepsilon _1}} \end{array}} \right. $ | (22) |
式中参数p、q和c可分别由试件上升段和下降段的试验数据回归分析得到,见表 4。
| 表 4 参数p、q和c回归分析结果 Tab. 4 Regression results of parameters p, q, and c |
基于上述提出的水泥基灌浆料统计损伤本构模型和弹性模量、峰值应力、峰值应变计算模型,可以计算给出早龄期水泥基灌浆料受压应力-应变全过程曲线,模型计算曲线与试验曲线对比结果见图 17。由图可见,计算曲线与试验曲线吻合程度较高,本文建议的统计损伤本构模型能够准确地表征早龄期水泥基灌浆料的受压应力-应变关系,损伤变量D能够较好地预测早龄期水泥基灌浆料试件的损伤演化过程。

|
图 17 模型计算结果和试验结果对比 Fig. 17 Comparison between calculated and test results |
通过对比不同龄期下水泥基灌浆料和同强度混凝土试件单轴受压试验结果,分析龄期对水泥基灌浆料和同强度混凝土试件受压应力-应变曲线特征参数的影响,得出如下结论:
1) 随龄期的增大,试件破坏时的“脆性”特征愈发明显,龄期3 d及以上的试件破坏时有碎片崩出,并伴有较大的崩裂声;与同强度混凝土相比,水泥基灌浆料加载时裂缝发展阶段持续时间较短,达到峰值荷载以后试件更易发生崩裂,迅速丧失承载力,破坏面平整、光滑,破坏后试件的整体性较差。
2) 随龄期的增长,试件峰值应力、峰值应变、极限应变、弹性模量、应变延性系数和能量耗散系数均有不同程度的增大;与同强度混凝土相比,水泥基灌浆料峰值应力发展较快,受压应力-应变曲线下降段较陡,峰值应力、峰值应变、极限应变、应变延性系数和能量耗散系数较大,而弹性模量、峰值割线模量较小。
3) 基于现有混凝土单轴受压本构模型,结合水泥基灌浆料自身特点,考虑龄期建立了修正的分段式水泥基灌浆料受压本构模型,模型计算结果与试验结果吻合较好。
4) 基于Weibull分布和对数正态分布建立了统计损伤本构模型,建议的统计损伤本构模型可以较准确地描述早龄期水泥基灌浆料的单轴受压应力-应变关系。
| [1] |
DOU Jinglei, DOU Jingfeng, GUO Yujuan. Researching on a new grouting material and its engineering application[J]. Advanced Materials Research, 2015, 1088: 544. DOI:10.4028/www.scientific.net/AMR.1088.544 |
| [2] |
SHANNAG M J. High-performance cementitious grouts for structural repair[J]. Cement & Concrete Research, 2002, 32(5): 803. DOI:10.1016/S0008-8846(02)00710-X |
| [3] |
汪刘顺, 汪秀石. 高性能水泥基灌浆料性能试验研究[J]. 低温建筑技术, 2012, 34(8): 10. WANG Liushun, WANG Xiushi. Experimental study on the performance of high performance cementitious grout[J]. Low Temperature Architecture Technology, 2012, 34(8): 10. DOI:10.3969/j.issn.1001-6864.2012.08.004 |
| [4] |
吴元, 王凯, 杨晓婧, 等. 水泥基灌浆料基本力学性能试验研究[J]. 建筑结构, 2014, 44(19): 98. WU Yuan, WANG Kai, YANG Xiaojing, et al. Experimental study on basic mechanical properties of cementitious grout[J]. Building Structure, 2014, 44(19): 98. |
| [5] |
汪秀石, 李树林, 吴元. 豆石型灌浆料的力学及变形性能试验研究[J]. 工业建筑, 2008(9): 83. WANG Xiushi, LI Shulin, WU Yuan. Experimental study of mechanical properties and deformability of pisolite grouting material[J]. Industrial Construction, 2008(9): 83. DOI:10.13204/j.gyjz200809024 |
| [6] |
陈大川, 林悦慈, 郭杰标, 等. 回弹法检测灌浆料早期强度的试验研究[J]. 铁道科学与工程学报, 2020, 17(1): 70. CHEN Dachuan, LIN Yueci, GUO Jiebiao, et al. Experimental study on testing the early strength of grouting material by rebound method[J]. Journal of Railway Science and Engineering, 2020, 17(1): 70. DOI:10.19713/j.cnki.43-1423/u.T20190258 |
| [7] |
陈大川, 李亮如, 彭勃, 等. 不同试模对灌浆料早期抗压强度影响试验研究[J]. 湖南大学学报(自然科学版), 2021, 48(5): 76. CHEN Dachuan, LI Liangru, PENG Bo, et al. Experimental study on influence of different test molds on early compressive strength of grouting materials[J]. Journal of Hunan University (Natural Sciences), 2021, 48(5): 76. DOI:10.16339/j.cnki.hdxbzkb.2021.05.009 |
| [8] |
余琼, 孙佳秋, 袁炜航. 带肋钢筋与套筒约束灌浆料黏结性能试验[J]. 哈尔滨工业大学学报, 2018, 50(12): 98. YU Qiong, SUN Jiaqiu, YUAN Weihang. Experimental study on bond behavior between ribbed steel bars and sleeve constrained grouting material[J]. Journal of Harbin Institute of Technology, 2018, 50(12): 98. DOI:10.11918/j.issn.0367-6234.201711108 |
| [9] |
余琼, 许雪静, 尤高帅. 带肋钢筋与灌浆料黏结性能试验[J]. 哈尔滨工业大学学报, 2017, 49(12): 91. YU Qiong, XU Xuejing, YOU Gaoshuai. Experimental study on bond behavior for ribbed steel bars and grout[J]. Journal of Harbin Institute of Technology, 2017, 49(12): 91. DOI:10.11918/j.issn.036706234.201701088 |
| [10] |
HU Xiaopeng, PENG Gang, NIU Ditao, et al. Bond behavior between deformed steel bars and cementitious grout[J]. Construction and Building Materials, 2020, 262: 120810. DOI:10.1016/j.conbuildmat.2020.120810 |
| [11] |
PENG Gang, NIU Ditao, HU Xiaopeng, et al. Experimental study of the interfacial bond strength between cementitious grout and normal concrete substrate[J]. Construction and Building Materials, 2021, 273(4): 122057. DOI:10.1016/j.conbuildmat.2020.122057 |
| [12] |
张可. 高性能灌浆料置换加固混凝土柱受力性能研究与应用[D]. 南昌: 南昌大学, 2018 ZHANG Ke. Study and application on property of reinforced concrete column strengthened by replacing section with high performance CGM[D]. Nanchang: Nanchang University, 2018 |
| [13] |
冷玉坤, 刘均利, 余文成, 等. 高强灌浆料加固既有RC梁抗弯性能分析[J]. 华侨大学学报(自然科学版), 2022, 43(1): 51. LENG Yukun, LIU Junli, YU Wencheng, et al. Flexural performance analysis of existing RC beams strengthened using high-strength grouting material[J]. Journal of Huaqiao University (Natural Science), 2022, 43(1): 51. |
| [14] |
吴元, 杨晓婧, 王凯, 等. 灌浆料单轴受压应力-应变曲线试验研究[J]. 工业建筑, 2014, 44(增刊): 912. WU Yuan, YANG Xiaojing, WANG Kai, et al. Experimental study on the stress-strain curve of cementitious grout under uniaxial compression[J]. Industrial Construction, 2014, 44(S): 912. DOI:10.13204/j.gyjz2014.s1.151 |
| [15] |
水泥基灌浆材料应用技术规范: GB/T 50448—2015[S]. 北京: 中国建筑工业出版社, 2015 Technical code for application of cementitious grout: GB/T 50448—2015[S]. Beijing: China Architecture and Building Press, 2015 |
| [16] |
混凝土物理力学性能试验方法标准: GB/T 50081—2019[S]. 北京: 中国建筑工业出版社, 2019 Standard for test method of mechanical properties on ordinary concrete: GB/T 50081—2019[S]. Beijing: China Architecture and Building Press, 2019 |
| [17] |
CEB—FIP(MC90): CEB—FIP model code 1990: design code[R]. Lausanne: Comité Euro-International du Béton, 1993
|
| [18] |
董军军. 高性能套筒灌浆料的研制及性能研究[D]. 合肥: 合肥工业大学, 2016 DONG Junjun. Development and properties of high performance cementitious grout for coupler[D]. Hefei: Hefei University of Technology, 2016 |
| [19] |
王凤, 刘焕玉, 王超杰. 龄期对钢筋套筒灌浆连接力学性能的影响[J]. 山东理工大学学报(自然科学版), 2020, 34(6): 75. WANG Feng, LIU Huanyu, WANG Chaojie. Effects of grout age on mechanical behavior of grout sleeve splicing[J]. Journal of Shandong University of Technology (Natural Science Edition), 2020, 34(6): 75. DOI:10.13367/j.cnki.sdgc.2020.06.015 |
| [20] |
过镇海. 钢筋混凝土原理[M]. 北京: 清华大学出版社, 2003: 15. GUO Zhenhai. Principle and analysis of reinforced concrete[M]. Beijing: Tsinghua University Press, 2003: 15. |
| [21] |
ACI Committee 363. State of the art report on high-strength concrete[J]. International Concrete Abstracts Portal, 1984, 81(4): 364. DOI:10.14359/10692 |
| [22] |
陈宗平, 张亚旗, 姚如胜, 等. 海砂混凝土单轴受压应力-应变全曲线试验研究[J]. 硅酸盐通报, 2019, 38(12): 3938. CHEN Zongping, ZHANG Yaqi, YAO Rusheng, et al. Experimental study on complete stress-strain curve of sea sand concrete behavior under uniaxial loading[J]. Bulletin of the Chinese Ceramic Society, 2019, 38(12): 3938. |
| [23] |
过镇海, 张秀琴, 张达成, 等. 混凝土应力-应变全曲线的试验研究[J]. 建筑结构学报, 1982, 3(1): 10. GUO Zhenhai, ZHANG Xiuqin, ZHANG Dacheng, et al. Experimental study on full stress-strain curves of concrete[J]. Journal of Building Structures, 1982, 3(1): 10. DOI:10.14006/j.jzjgxb.1982.01.001 |
| [24] |
CARREIRA D J, CHU K H. Stress-strain relationship for plain concrete in compression[J]. Journal of the American Concrete Institute, 1985, 82(6): 797. DOI:10.1016/0022-3115(85)90362-9 |
| [25] |
WEE T H, CHIN M S, MANSUR M A. Stress-strain relationship of high-strength concrete in compression[J]. Journal of Materials in Civil Engineering, 1999, 11(1): 27. DOI:10.1061/(ASCE)0899-1561(1999)11:1(21) |
| [26] |
混凝土结构设计规范: GB 50010—2010[S]. 北京: 中国建筑工业出版社, 2010 Code for design of concrete structures: GB 50010—2010[S]. Beijing: China Architecture and Building Press, 2010 |
| [27] |
KACHANOV M, MONTAGUT E. Interaction of a crack with certain microcrack arrays[J]. Engineering Fracture Mechanics, 1986, 25(5): 625. DOI:10.1016/0013-7944(86)90028-7 |
| [28] |
LEMAITRE J. How to use damage mechanics[J]. Nuclear Engineering and Design, 1984, 80(2): 233. DOI:10.1016/0029-5493(84)90169-9 |
| [29] |
LI Jie, REN Xiaodan. Stochastic damage model for concrete based on energy equivalent strain[J]. International Journal of Solids and Structures, 2009, 46(11/12): 2407. DOI:10.1016/j.ijsolstr.2009.01.024 |
| [30] |
BENALLAL A, BILLARDON R, LEMAITRE J. Failure analysis of structures by continuum damage mechanics[J]. Fracture, 1984, 3669. DOI:10.1016/B978-1-4832-8440-8.50397-5 |
| [31] |
吴政, 张承娟. 单向荷载作用下岩石损伤模型及其力学特性研究[J]. 岩石力学与工程学报, 1996, 15(1): 56. WU Zheng, ZHANG Chengjuan. Investigation of rock damage model and its mechanical behaviour[J]. Chinese Journal of Rock Mechanics and Engineering, 1996, 15(1): 56. DOI:10.3321/j.issn:1000-6915.1996.01.008 |
| [32] |
LIU Xi, WU Tao, LIU Yang. Stress-strain relationship for plain and fibre-reinforced lightweight aggregate concrete[J]. Construction and Building Materials, 2019, 225: 270. DOI:10.1016/j.conbuildmat.2019.07.135 |
 2022, Vol. 54
2022, Vol. 54


